SVM支持向量机(1)

一、SVM模型

　　1.函数间隔与几何间隔，哪一条线是最好的？

　　　

　　　　(1)公式化问题。

　　　　　　分类模型：当里面的值小于0的时候就是-1，当里面的值是大于等于0的时候就是1

　　　　　　　　

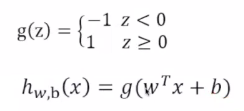
　　　　　　函数间隔：前面乘以y(i)，是为了保持数值为正值，数据点到直线的距离。把点代进去就是其函数间隔，函数间隔最好的是几何间隔最大的那个。最好的分类线就是几何间隔最大的分类线

　　　　　　　　

　　　　　　我们要找到最好的直线，对每个数据点都计算出函数间隔，对于一个直线而言可以计算出最小函数间隔，这个最小的函数间隔可以判断直线和数据集的拟合程度。

　　　　　　只要成倍的增大w和b值，函数间隔就能无限增大。-1和1的二阶范数是根号2

　　　　　　

　　　　　　几何间隔：

　　　　

　　　　　　初始函数表达式:最大化集合间隔，使得所有的数据点都大于等于这个集合间隔，||w||二阶范数就是欧氏距离，两点相减然后求二阶范数，就是法向量的求法。

　　　　　　

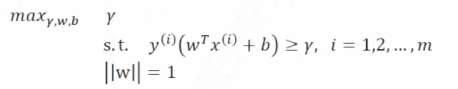
　　初始函数表达式　　

　　

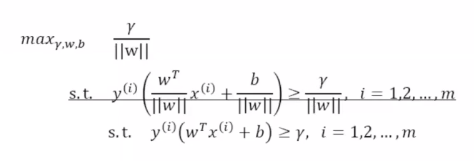
　　　　　　非凸性约束，容易达到局部最优。

　　　　

　　　　核心思想：我们要找到一个分类面，使得在线性可分的时候，这条直线是最好的。一个最好的分类线就是几何间隔最大的分类线。

　　　　　　　　　　点到直线的距离可以理解为置信度，当点离分类界面越远的时候，

　　　　　　　　　　那么点对分类的置信度比较高，当点比较接近直线边缘的时候，点对分类的置信度比较低。

　　　　简化步骤1：令||w||=1，范数是1代表是集合间隔，伽马是几何间隔，最大化几何间隔，使得所有的数据点大于等于这个几何间隔，同时w的范数大于等于1，二阶范数是欧氏距离，即两个点相减然后求解二阶范数，二阶范数和欧氏距离没有什么关系，二阶范数是求解欧氏距离的一个手段，二阶范数即对于每个向量都求平凡，把每个分量加起来求根号。将函数间隔变为几何间隔。

　　　　

　　

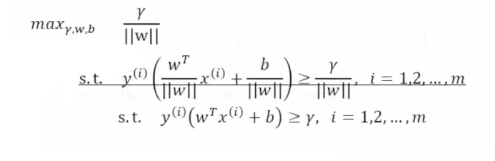
　　　　简化步骤2：调整w和b，将r变为1，所以索性直接变为1，将最大化的调整变为最小化问题。

　　　　

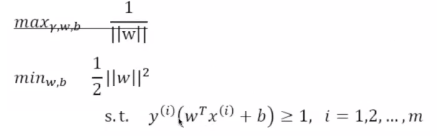
　　　　最终问题：变成调整w和b使得w的二阶范数的平方是最小的，最小化w的范数和最小化w的范数是一个意思。使得下面的条件得到满足

　　　　　　

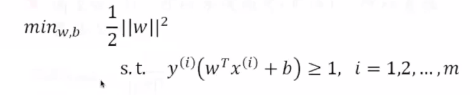
　　　　线性约束下优化二次函数

　　　　　　有数学方法可以 解决这个问题，可以引入对偶函数

　　2.最优间隔分类器

　　3.拉格朗日求解

　　　(1)最小化一个f(w)，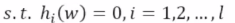

　　　(2)构造拉个朗日函数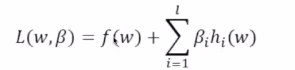

　　　(3)求解：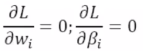

　　　(4)有不等式约束的时候：在广义上面可以引入一个不等的关系，

　　　　

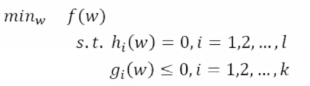
　　　(5)拉格朗日方程：

　　　　

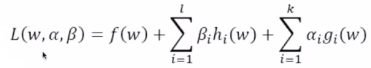
　　　(6)极小极大：先对变换后的拉格朗日函数求出极大值，先调整a,b，如果都满足条件的话，hi(w)=0，gi(w)是小于等于0的。这里不管如何调整a,b，其最大值都应该是0，当某个条件不允许的时候hi(w) 不等于0，那么可以调整b，使得b调整的特别大，就可以使得其为一个正无穷大。

　　极小极大问题的最优解：在后面会使用到。

　　　

　　　　(7)广义拉个朗日函数

　　　　　　对偶问题与原始问题的等价性：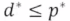

　　　　　　约束不等式g都是凸函数：线性函数都是凸函数

　　　　　　约束等式h都是仿射函数：仿射和线性等价，除了允许截距b

　　　　　　不等式严格执行：必有g不等式是小于0的

　　　

　

　　　　

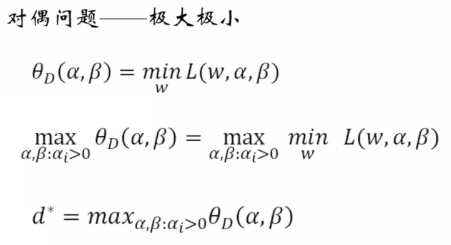
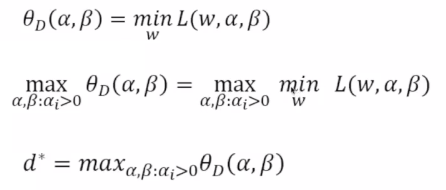
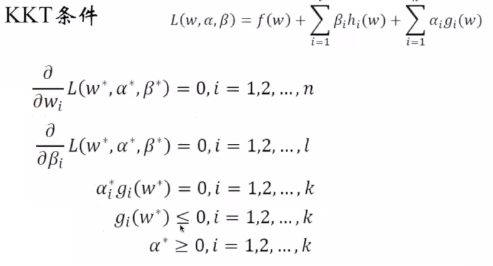
　　4.最优间隔分类器求解

　

　　　　

　

　　　　

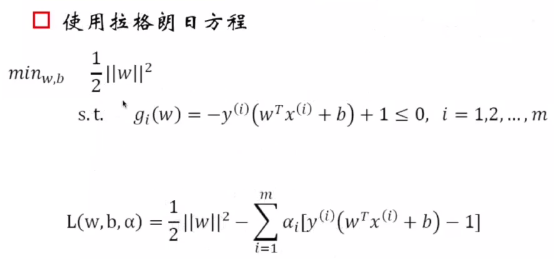
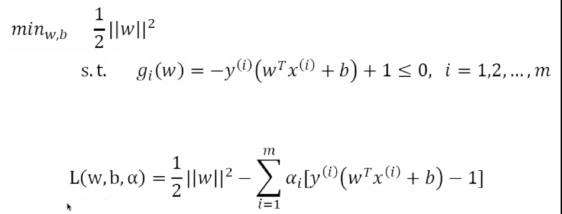
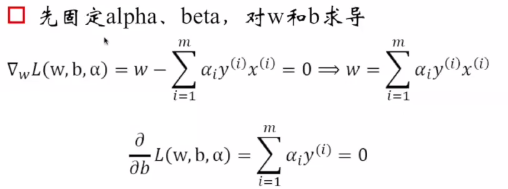
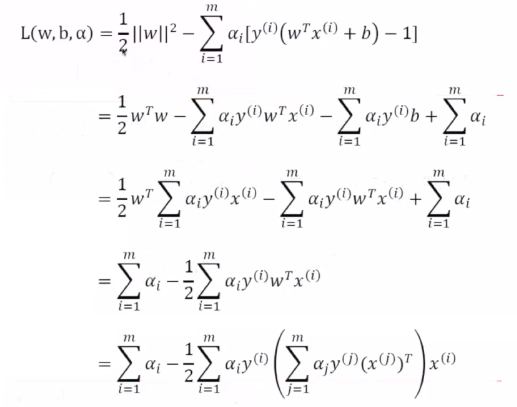
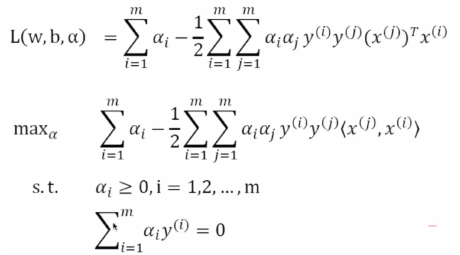
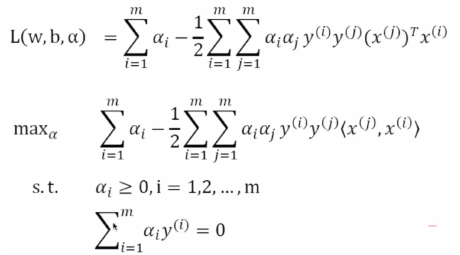
　　最优间隔分类器求解

　　　　

　　5.SMO算法

　　　　坐标上升法：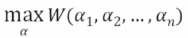

　　

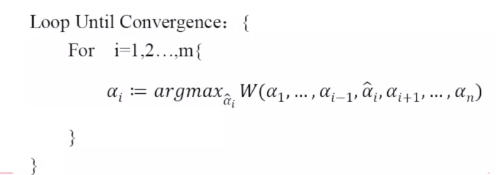
　　　　二维坐标上升法：先调整一个维度上的，再去调整另外一个轴上的值，

　　　　

　　

　　　　

　　6.核技法

　　

　　　　

　　7.软间隔分类器

　　8.合页损失函数

　　9.多分类

二、SVM实战文本分类