【学术篇】CF833B TheBakery 分治dp+主席树

题目の传送门~

题目大意: 将\(n\)个蛋糕分成恰好\(k\)份, 求每份中包含的蛋糕的种类数之和的最大值.

这题有两种做法. 第一种是线段树优化dp, 我还没有考虑. 另一种就是分治+主席树.

然后如果看到分治+主席树的话 可以看成是两道题的二合一~

不过ADAMOLD正解应该是有\(O(nk)\)做法的吧, 我的\(O(nklogn)\)分治好像被卡了一点常数QwQ

首先我们可以非常容易的看出这题要用dp和状要用到的状态转移方程

\[f[i][j]=max{f[i-1][k]+d(k+1,j)}\ (k\in[1,j))
\]

那么很显然我们已经可以\(O(n^2k)\)做了. 但是这显然过不去, 我们必须要优化.

优化的方式有两种, 就是上面提到的线段树或者分治.

分治的话就是非常套路的东西了, 专门用来应对\(f[i][j]=f[i-1][k]+w(i,j)\), 其中费用函数\(w\)没啥特殊性质的情况的dp.

通常情况下, 我们观察每次要转移\(f[i][j]\)时令转移最优的\(A[i][j]\), 会发现有

\[A[i, j - 1] \leq A[i, j]\leq A[i + 1, j]
\]

啥意思呢就是这破玩意是单调的.所以我们假如我们求出\(f[i][mid]\)要在\(k\)处转移, 我们就知道\(f[i][1..mid-1]\)的转移点是在\((1,k)\)的了.

这样我们就有了一个分治的形式, 就可以直接做了. 而这类分治dp是有套路的(又到了py式伪代码时间

def solve(x,l,r,L,R): # 处理f[x][l]..f[x][r]这一堆的dp值, 转移点落在[L,R]
    if l<=0 or l>r or r<=0 or r>n: # xjb写一通反正就是如果越界就不处理了
         return
    if x==1: # f[1]的情况作为边界条件显然要特殊处理.
        for i  in range(l,r+1):
            f[x][i]=w(i,1)
    f[x][i]=INF # 这里的INF表示反向极限值(就是你要求min的话就是最大值
    g[x][i]=L
    for i in range(L,R+1):
        if f[x-1][i]+w(i+1,mid)>f[x][mid]: # 自然是对f[x][mid]进行转移啦~
            f[x][mid]=f[x-1][i]+w(i+1,mid) # 注意这里的i+1如果>mid的话要返回非法值(比如INF
            g[x][mid]=i # 标记最优的转移位置供继续分治使用
    solve(x,l,mid-1,L,g[x][mid]) # 递归处理左半边
    solve(x,mid+1,r,g[x][mid],R) # 递归处理右半边

for i in range(1,k+1): # 第一维1~k都要做一遍..
    solve(i,1,n,1,n)

就可以啦, 每个题的区别就在求w(i,j)的部分了.

可以证明, 这个分治的过程每层是\(O(nlogn)\)的(反正窝不会证), 从1~k各扫一遍就是\(O(nklogn)\)的了.

对于ADAMOLD来说, 自然用\(O(n^2)\)预处理二维前缀和搞一下就ok了. (但是\(O(nklogn)\)有点卡常数?!

然后这个题的w(i,j)就是表示[i,j]区间内的蛋糕的种类数.

那么静态询问区间种类数的话我们就可以去看下DQUERY这道题咯(明显的模板题)

由于我并不认为这题可以离线, 所以树状数组或莫队是简明不行的. 我们要用主席树.

我们对每个时刻开一个\(n\)个节点的线段树, 然后用一个map记录每个数上一次出现的位置.

如果在第\(i\)个位置遇到一个没出现过的数\(x\), 我们把第\(i\)棵树的\(i\)位置+1.

如果遇到一个出现过的数\(y\), 我们先在第\(i\)棵树上把它上一次出现的位置\(last_y\)-1, 然后\(i\)位置+1,

这样就可以保证每个重复的数只存在于最后一次出现的位置,

这时候第\(i\)棵线段树就表示第\(i\)个时刻每个位置上不同的数的个数了.

我们可以画图来更好的体会这一点, 以DQUERY的样例为例,

5

1 1 2 1 3

首先我们要建一个有\(n\)个叶子节点的线段树(啊啊啊我画的图好丑啊 大家凑合看看, 意会一下?



我们在1位置遇到了一个1, 1还从来没有出现过, 我们让1 +1, 然后把\(last_1\)设成1.



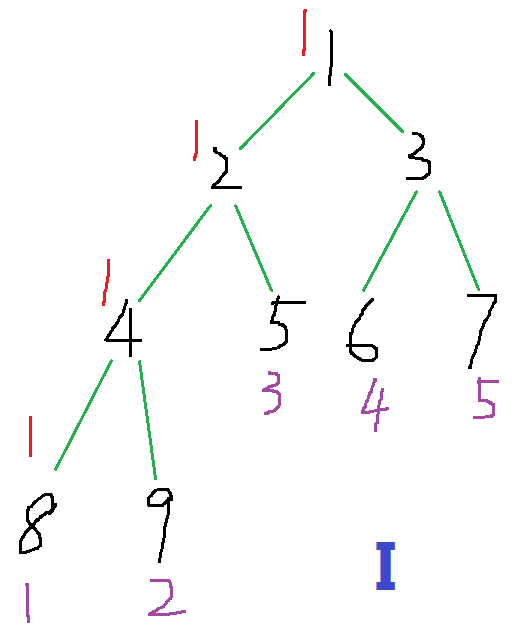
我们在2位置又遇到了一个1, 1出现过了, 我们让\(last_1\)(1) -1, 然后让2 +1, 把\(last_1\)设成2.



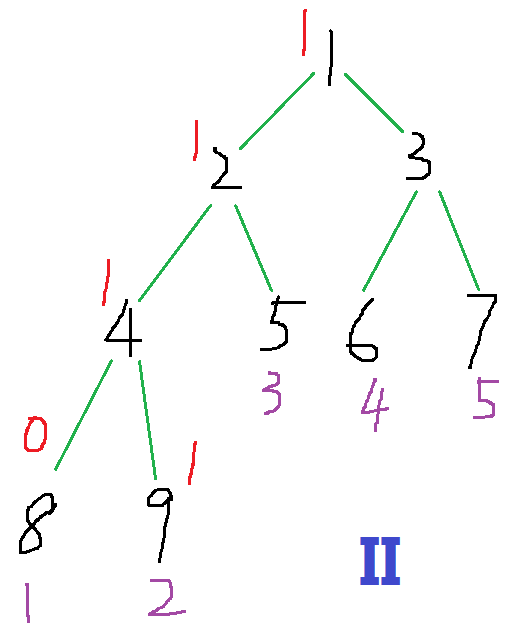
我们在3位置遇到一个2, 2没出现过, 3 +1, \(last_2=3\)



我们在4位置又双叒叕遇到一个1, \(last_1\)(2) -1, 4 +1,\(last_1=4\)



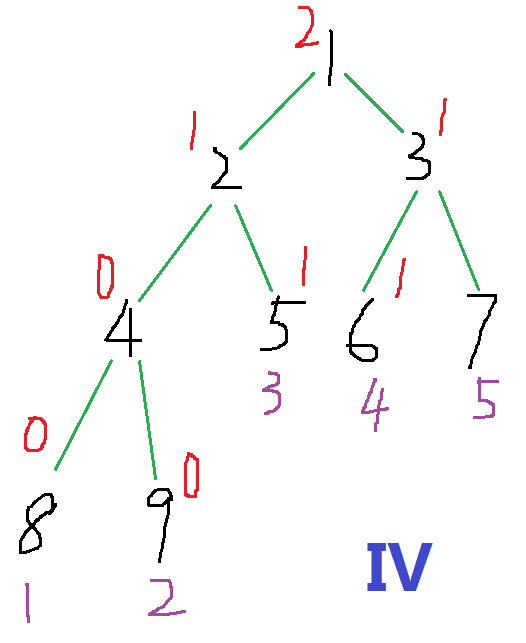
5位置遇到一个3, 5 +1, \(last_3=5\)



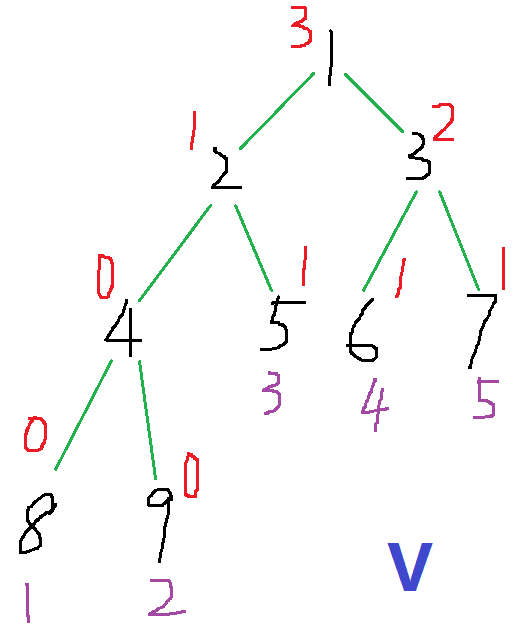
这样我们就建好静态的主席树了, 我们看一下, 是不是第\(i\)棵树对应着第\(i\)个时刻的种类情况呢~

这样我们查询\([L,R]\)这个区间的时候, 就只需要在第\(R\)棵树上查\(L\)点及以后的和就完了OwO

单次查询都是\(O(logn)\)的

然后我们就解决了分治时候算\(w(i,j)\)的问题, 现在的时间复杂度应该是\(O(nklogn)*O(logn)=O(nklog^2n)\)的.

可以通过本题了, 虽然复杂度比线段树优化的\(O(nklogn)\)要多个log, 但是实际情况并没有慢太多(都是朴素实现大约慢一倍?

不过(可能?)要好写一点..

代码:

#include <cstdio>
#include <unordered_map>
std::unordered_map<int, int> mp;
const int N=36005;
struct node{int sum,l,r;}t[N<<5];
int f[55][N],g[55][N],rt[N],n,k,tot;
inline int gn(int a=0,char c=0){
	for(;c<'0'||c>'9';c=getchar());
	for(;c>47&&c<58;c=getchar()) a=a*10+c-48;
return a;}
void update(int &x,int l,int r,int pre,int pos,int val){
	t[++tot]=t[pre]; x=tot; t[x].sum+=val;
	if(l==r) return; int mid=(l+r)>>1;
	if(pos<=mid) ::update(t[x].l, l, mid, t[pre].l, pos, val);
	else ::update(t[x].r, mid+1, r, t[pre].r, pos, val);
}
int query(int x,int l,int r,int L){
	if(L<=l) return t[x].sum;
	int mid=(l+r)>>1;
	if(L<=mid) return ::query(t[x].l, l, mid, L)+t[t[x].r].sum;
	return ::query(t[x].r, mid+1, r, L);
}
inline int qquery(int l,int r){
	if(l>r) return 0x7fffffff;
	return ::query(rt[r], 1, n, l);
}
void solve(int x,int l,int r,int L,int R){
	if(l<=0||l>r||r<=0||r>n) return;
	if(x==1){
		for(int i=l;i<=r;++i)
			f[x][i]=::qquery(1, i);
		return;
	} int mid=(l+r)>>1,maxn=0;
	f[x][mid]=0;; g[x][mid]=L;
	for(int i=L;i<=R;++i){
		maxn=f[x-1][i]+::qquery(i+1, mid);
		if(maxn>f[x][mid])
			f[x][mid]=maxn,g[x][mid]=i;
	}
	solve(x,l,mid-1,L,g[x][mid]);
	solve(x,mid+1,r,g[x][mid],R);
}
int main(){ n=gn(); k=gn(); int tmp;
	for(int i=1;i<=n;++i){
		int x=gn();
		if(mp.find(x)==mp.end())
			::update(rt[i], 1, n, rt[i-1], i, 1);
		else{
			::update(tmp, 1, n, rt[i-1], mp[x], -1);
			::update(rt[i], 1, n, tmp, i, 1);
		}
		mp[x]=i;
	}
	for(int i=1;i<=k;++i)
		::solve(i, 1, n, 1, n);
	printf("%d",f[k][n]);
}

对 就是这样咯~