Pytorch笔记 (1) 初始神经网络

一、人工神经元

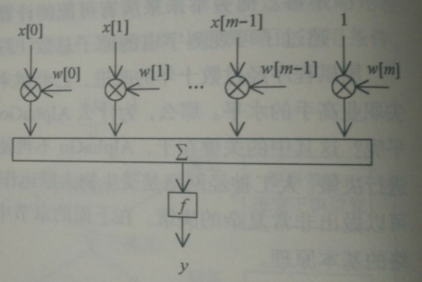
上方人工神经元中：

1. 输入 * 权重 ——>  相当于 人神经元中  树突的功能
2. 各输入 相加 ，再做非线性变化f ——>  相当于胞体的功能
3. 将非线性变化的结果输出 ——> 相当于轴突

在非线性函数f固定的情况下，选择不同的权重，单个神经元 可以完成 不同的运算

但并不是全部，比如 ： “或运算”

上述证明过程 可表示为： y = f( w[0] * x[0] + w[1] * w[1] + w[2]  )

在 x[0] x[1] 两个输入 分别为 00  10   01   11  的情况下，最终的输出为 y = 0 1 1 1【或运算】

利用反证法 证明

二、人工神经网络

指多个神经元 ——>  组成的网络

【其中，某些神经元的 输出 会 作为 另外一些神经元的输入】

比如，用两个 权重不同的 神经元搭成的神经网络 实现或运算

神经网络可以模拟所有可能的运算

证明： 由非线性函数为 f() = max(.,0)的神经元组成的神经网络 可以模拟 任何闭区间上的连续分段线性函数

如果输入和输出直接的关系 不是分段 线性函数，还能不能用 神经网络模拟？ ———— 当然可以

原因：  任意一个 输入/输出关系 都可以用分段线性函数来近似，只要分段点足够多，就可以非常准确地用 分段函数 来近似这个函数。而 分段线性函数，可以通过人工神经网络搭建来得到————>  只要人工神经网络 中的神经元 数目足够多，神经元之间的关系 足够复杂，就可以非常精确的模拟任意的 输入/ 输出关系    【即，万能近似定理】

三、神经网络的设计和权重的学习

1. 神经网络结构的确定：    神经元个数越多，链接越复杂，能便是的 输入/输出 关系越多，对特定 输入/输出关系的表达 就 越精确，但也就越难找到 最合适的权重------最优的输入/输出关系   【中间 存在 折中关系】
2. 神经网络中神经元权重的确定：         权重的选取  可以看作  是一个 优化问题 。  对于每一组确定的权重值，我们可以确定出优化问题的 收益或损失。当权重不合适时，优化问题的收益笑，损失大；权重合适时，优化问题的收益大，损失小   【通过调节权重，最大化收益，最小化损失，就可以得到合适的权重】