vtkTestHull将多个平面围成一个凸面体

1、vtkHull

produce an n-sided convex hull

vtkHull is a filter which will produce an n-sided convex hull given a set of n planes. (The convex hull bounds the input polygonal data.) The hull is generated by squeezing the planes towards the input vtkPolyData, until the planes just touch the vtkPolyData. Then, the resulting planes are used to generate a polyhedron (i.e., hull) that is represented by triangles.

The n planes can be defined in a number of ways including 1) manually specifying each plane; 2) choosing the six face planes of the input's bounding box; 3) choosing the eight vertex planes of the input's bounding box; 4) choosing the twelve edge planes of the input's bounding box; and/or 5) using a recursively subdivided octahedron. Note that when specifying planes, the plane normals should point outside of the convex region.

The output of this filter can be used in combination with vtkLODActor to represent a levels-of-detail in the LOD hierarchy. Another use of this class is to manually specify the planes, and then generate the polyhedron from the planes (without squeezing the planes towards the input). The method GenerateHull() is used to do this.

Tests:

vtkHull (Tests)

下面分别是有50个和150个随机面围裹成的两个凸多面体

    

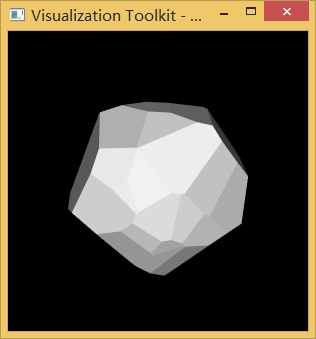
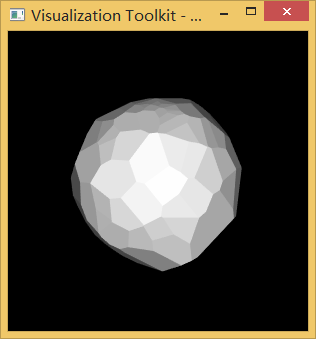
示例代码：

#ifndef INITIAL_OPENGL
#define INITIAL_OPENGL
#include <vtkAutoInit.h>
VTK_MODULE_INIT(vtkRenderingOpenGL)
VTK_MODULE_INIT(vtkInteractionStyle)
#endif
#include <iostream>
using namespace std;
#include <vtkVersion.h>
#include <vtkActor.h>
#include <vtkLine.h>
#include <vtkPointData.h>
#include <vtkPoints.h>
#include <vtkPolyData.h>
#include <vtkPolyDataMapper.h>
#include <vtkRenderer.h>
#include <vtkRenderWindow.h>
#include <vtkRenderWindowInteractor.h>
#include <vtkSmartPointer.h>
#include <vtkFloatArray.h>

#include <vtkMath.h>
#include <vtkPlanes.h>
#include <vtkHull.h>

int main()
{
    vtkSmartPointer<vtkMath> mathObj=vtkSmartPointer<vtkMath>::New();
    vtkSmartPointer<vtkPoints> points=vtkSmartPointer<vtkPoints>::New();
    vtkSmartPointer<vtkFloatArray> normals=vtkSmartPointer<vtkFloatArray>::New();
    normals->SetNumberOfComponents();
    float radius,theta,phi,x,y,z;
    int numberOfPlanes=;
///创建numberOfPlanes个随机平面，每个平面中心点坐标为(x,y,z)，其法向量为(x,y,z)，
///无论怎样随机，这些平面都是与半径为radius的球面相切，并包裹着该球面
    for(int i=;i<numberOfPlanes;i++)
    {
         radius=;
        theta=mathObj->Random(,mathObj->Pi()*);
        phi=mathObj->Random(,mathObj->Pi());
        x=radius*sin(phi)*cos(theta);
        y=radius*sin(phi)*sin(theta);
        z=radius*cos(phi);
        points->InsertPoint(i,x,y,z);
        normals->InsertTuple3(i,x,y,z);
    }
    vtkSmartPointer<vtkPlanes>planes=vtkSmartPointer<vtkPlanes>::New();
    planes->SetPoints(points);
    planes->SetNormals(normals);
std::cout<<planes->GetNumberOfPlanes()<<std::endl;
    vtkSmartPointer<vtkHull>hull=vtkSmartPointer<vtkHull>::New();
    hull->SetPlanes(planes);
   vtkSmartPointer<vtkPolyData> pd=vtkSmartPointer<vtkPolyData>::New();
    hull->GenerateHull(pd,-,,-,,-,);

    vtkSmartPointer<vtkPolyDataMapper>hullMapper=vtkSmartPointer<vtkPolyDataMapper>::New();
    hullMapper->SetInputData(pd);

    vtkSmartPointer<vtkActor>hullActor=vtkSmartPointer<vtkActor>::New();
    hullActor->SetMapper(hullMapper);
    //创建图形对象
    //创建显示窗口
    vtkSmartPointer<vtkRenderer> ren1=vtkSmartPointer<vtkRenderer>::New();
    vtkSmartPointer<vtkRenderWindow> renWin=vtkSmartPointer<vtkRenderWindow>::New();
    vtkSmartPointer<vtkRenderWindowInteractor> iren=vtkSmartPointer<vtkRenderWindowInteractor>::New();
    ren1->AddActor(hullActor);
    renWin->AddRenderer(ren1);
    iren->SetRenderWindow(renWin);

    ren1->ResetCamera();
    iren->Initialize();
    iren->Start();

    return ;
}