模拟赛DAY 2 T1江城唱晚

【题目背景】

墙角那株海棠，是你种下的思念。

生死不能忘，高烛照容颜。

一曲江城唱晚，重忆当年坐灯前，

青衫中绣着你留下的线。

——银临《江城唱晚》

【问题描述】

扶苏是个喜欢一边听古风歌一边写数学题的人，所以这道题其实是五三原题。

歌曲中的主人公看着墙边的海棠花，想起当年他其实和自己沿着墙边种了一排海

棠，但是如今都已枯萎，只剩下那一株，寄托着对他深深的思念。

沿着墙一共有 n 个位置可以种下海棠花，主人公记得自己当年和他一共种下了 m

朵，由于花的特性，海棠不能紧挨着种植，也就是两朵海棠花之间最少间隔一个不种花

的空位置。但是她记不清当时海棠花具体是怎么摆放的了，所以她想知道一共有多少方

案使得 m 朵海棠花都被种下且两两之间不是相邻的。我们将这 m 朵海棠花按照

1,2,3…m 的顺序编号，两个种花的方案不同当且仅当它们被种下的位置不同或者从左向

右数花的编号序列不同。

为了避免输出过大，答案对一个参数 p 取模

【输入格式】

输入文件名为 ilove.in。

输入文件中有且仅有一组数据，只有一行四个数字，分别代表 type,n,m,p。其中

type 是一个帮助你判断测试点类型的参数，会在数据范围中说明。

【输出格式】

输出文件名为 ilove.out。

输出一行一个数字，代表答案对 p 取模的结果。

 

【输入输出样例 1】

ilove.in	ilove.out
1 3 2 19260718	2

见选手文件夹下的 Samples/ilove/ilove1.in 和Samples/ilove/ilove1.ans。

【输入输出样例1解释】

一共有两朵花，3 个位置。如果给花朵编号为 1,2，位置编号为 1,2,3，那么两种方案分别如下：

位置	1	2	3
方案1	花朵1	N/A	花朵2
方案2	花朵2	N/A	花朵1

【输入输出样例 2】

见选手文件夹下的 Samples/ilove/ilove2.in 和Samples/ilove/ilove2.ans。

【数据规模与约定】

本题共 5 个子任务，捆绑测试，各子任务不等分。各子任务的数据性质如下表

子任务编号	n≤	m≤	type=	特殊性质	子任务分值
1	1	1	0	特殊性质1	5
2	20	20	1		15
3	400	200	2	无	20
4	2000	1000	3
5	2000000	1000000	4	特殊性质2
6			5	无

特殊性质1：保证对应测试点的实际方案数(在取模之前)不超过10⁶

特殊性质2：保证对应测试点的模数 p 是一个质数。定义整数 x 为一个质数当且仅当 x 有且仅有 1 和 x 两个因数。

---

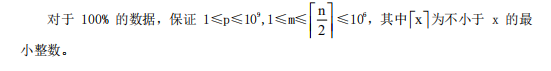
题解：

我们现在有n个位置，放m个物品，考虑把放了物品的位置拿出来，还剩下n-m个空着的位置（这些位置是不能放东西的），然后把这m个物品插入到这n-m个位置所夹的空位里面（插空法），加上两边一共n-m+1个位置，所以所有放的位置的情况就是C_n-m+1^m然后在乘上他自己的全排列A_m^m，化简之后就是!(n-m+1)/!(n-2m+1)=∏_n-2m+2^n-m+1

代码。。。

都化简成这样了，还不会吗QωQ