洛谷 P1169 棋盘制作 题解

题面

这道题可以分成两部分来处理；

第一部分：

设f[i][j]表示右下角以(i,j)结尾的最大正方形的边长。

显然f[i][j]=min(f[i][j-1],f[i-1][j-1],f[i-1][j])+1

第二部分:

可以使用悬线法进行解决。

定义：

有效竖线：除了两个端点外，不覆盖任何障碍点的竖直线段。

悬线：上端点覆盖了一个障碍点或达到整个矩形上端的有效竖线。如图所示的三个有效竖线都是悬线

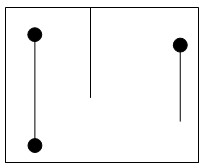
如果将一个悬线向左右两个方向尽可能移动所得到的有效子矩形称为这个悬线所对应的子矩形，那么所有悬线所对应的有效子矩形的集合一定包含了所有极大子矩形的集合。

可以发现，通过枚举所有的悬线，就可以枚举出所有的极大子矩形。由于每个悬线都与它底部的那个点一一对应，所以悬线的个数＝(n-1)×m（以矩形中除了顶部的点以外的每个点为底部，都可以得到一个悬线，且没有遗漏）。如果能做到对每个悬线的操作时间都为O(1)，那么整个算法的复杂度就是O(NM)。这样，我们看到了解决问题的希望。

对于一个底部为(i,j)的悬线，设它的高为hight[i,j],左右最多能移动到的位置为left[i,j],right[i,j]。

如果点(i,j)为障碍点，则：

height[i,j]=1;

left[i,j]=j;

right[i,j]=j;

如果点(i,j)不是障碍点，则：

height[i,j]=height[i-1,j]+1;

left[i,j]=max( left[i-1,j] , left[i,j])(左边第一个障碍点位置,边界0也是障碍点 );

right[i,j]=min( right[i-1,j] , right[i,j])(右边第一个障碍点位置,边界m也是障碍点 );

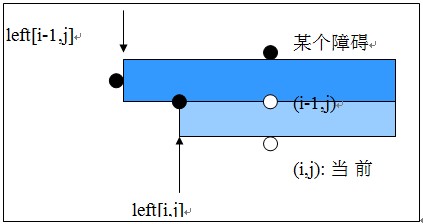
这样做充分利用了以前得到的信息，使每个悬线的处理时间复杂度为O(1)。对于以点(i,j)为底的悬线对应的子矩形，它的面积为(right[i,j]-left[i,j]+1)*height[i,j]。

Result＝max(right[i,j]-left[i,j])*height[i,j] (l<=i<n, l<=j<=m)

整个算法的时间复杂度为O(NM)，空间复杂度是O(NM)。