【五一qbxt】test1

（不知道为什么居然爆零了qwq）

（全员爆零诶，最高分10分？？？还是rand出来的？？？）

我freopen写错了？？？？自闭了

不行不行再写一遍freopen加深印象，不能再写错了

freopen("文件名","r",stdin);
freopen("文件名","w",stdout);

行吧，还是来整一整老师给的题解吧qwq

忍不住bibi一句出题的这个哥哥好年轻啊qwq，我都不好意思叫人家老师，应该是哥哥

---

题目

Problem A.最近公共祖先

先列一个表格

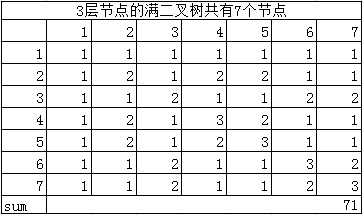
这样大概就理解71是怎么出来的了

30pts思路：

将整棵树建出，共有 O(Kⁿ) 个节点，计算任意两个节点的LCA 复杂度 O(n)。

注意到没有必要将所有点对的 LCA 都计算出来， 因为对于同一层的两个节点 u 和 v，

∑ _i ∈T depth(lca(i, u)) 和 ∑ _i ∈Tdepth(lca(i, v)) 是相同的， 每一层只需要算一个节点就行， 时间复杂 度 O(n²K ⁿ) 。

（以上是老师的思路，但是我现在对建树这种事有点蒙？？？当时考试的时候爆零了qwq，实际上我的暴力也是可以得30分的。下次一定得记得开long long）

先带上一个七十多行的大暴力：

30分代码：
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define mo 998244353

using namespace std;

long long k,n,ans,s,z;
int t[];

struct c{
    int num1,num2;
   //num1表示以这一层为根的子树的结点数
   //num2表示这一层的结点数
}ceng[];

int quick_pow(int a,int b) { //快速幂
    int ans=;
    if(b==)return ;
    while(b){
        if(b&)ans=(a*ans)%mo;
        a=(a*a)%mo;
        b/=;
    }
    return ans%mo;
}

int num1(int n,int k){//求子树点数 n层k叉树
    int z=n-;
    int num=;
    while(z){
        num+=quick_pow(k,z);
        z--;
    }
    return num+;
}

void ych(){
    for(int i=;i<=n;i++){
        ceng[n-i+].num1=num1(i,k);//以这一层为根的子树的结点数
        ceng[i].num2=quick_pow(k,i-);//这一层的结点数
    }

}

int main(){

    scanf("%d%d",&n,&k);

    ych();//他本来叫做预处理，后来被我改成了于才鸿

    for(int i=;i<=n;i++)
        ans+=num1(n-i+,k)*quick_pow(k,i-)*i;//求的是子树的
       //这里算的是某个点以下的depth之和包括它自己

    for(int i=;i<=n;i++)
        s+=i*quick_pow(k,i-);//这里算的是每个点自己的depth和

    ans-=s;
    ans=ans*%mo;

    for(int i=;i<=n;i++){
        for(int j=;j<i;j++){
            z+=(k-)*ceng[i-j+].num1*(i-j)*quick_pow(k,i-);
//算的是同一深度的
        }
    }

    ans+=z;
    ans%=mo;

    cout<<(ans+s)%mo<<endl;
    return ;
}

60pts思路:

更一般的，题目计算的是任意两个点 LCA 的深度，这个数量等于，任意两个点公共的祖先共有多少个。考虑计算第 i 层的某个节点，是多少个点对的公共祖先，这个数量就是该节点子树内节点数的平方。第 i 层的节点所在子树节点数 1+K+···+K ⁿ⁻ⁱ=（Kⁿ⁻ⁱ⁺¹−1）/(K−1) 。答案就是 ∑ⁿ _i=1 ( （Kⁿ⁻ⁱ⁺¹−1）/（K−1） ) ² ∗ K ⁱ⁻¹

即：

求任意两点LCA深度=>任意两点公共祖先数量=>a是多少个点对的公共祖先（枚举对于每个数a，它是x，y的公共祖先=>x，y在a的子树里。有多少个点在a的子树中呢？）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
const int mo=;

using namespace std;

long long ans,k1;

int n;

long long pow(long long a,int b){
    long long ans=;
    if(b==)return ;
    while(b){
        if(b&)ans = (a*ans)%mo;
        a = (a*a)%mo;
        b/=;
    }
    return ans%mo;
}

int main(){
    scanf("%d%lld",&n,&k1);

    for(int i=;i<=n;i++)
        ans=(ans+pow((long long)(pow(k1,n-i+)-)%mo*pow(k1-,mo-)%mo,)*pow(k1,i-))%mo;
//核心式子的编程语言

    cout<<ans%mo<<endl;
}

100pts思路：

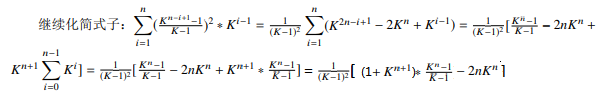
#include <bits/stdc++.h>

using namespace std;

const int mod = ;
typedef long long LL;
int fpm(int p, int k)
{
    int res = ;
    for (p %= mod; k; k >>= , p = (LL) p * p % mod)
        if (k & ) res = (LL) res * p % mod;
    return res;
}
int main()
{
//    freopen("lca.in", "r", stdin);
//    freopen("lca.out", "w", stdout);
    int n, K; cin >> n >> K;
    int e = fpm(K - , mod - ); //e=1/(K-1)
    int x = (fpm(K, n) - ) * (LL) e % mod; //x=(K^n-1)/(K-1);
    int ans = (fpm(K, n + ) + ) * (LL) x % mod;//ans=(K^(n+1)+1)*((K^n-1)/(K-1))
    ans = (ans -  * n * (LL) fpm(K, n)) % mod;//ans=(K^(n+1)+1)*((K^n-1)/(K-1))-2nK^n;
    ans = ans * (LL) e % mod * (LL) e % mod;//ans*=(1/(K-1))^2;
    cout << (ans <  ? ans + mod : ans);//三目运算符，判断是否为负数
}

Problem2：最长公共回文子序列：

50pts思路：

经典的做法：

设s，t的反串（eg：abbsf 反串fsbba）为s^r，t^r，那么求s和t的最长公共回文序列就是求s，s^r，t，t^r的最长公共子序列。

---

如何求最长公共子序列？

用DP！

怎么用？

粘一篇别人的博客吧：链接

对于二维的转移方程：

dp[i][j]=   dp[i-1][j-1]   s[i]=t[j];

max{dp[i-1][j],dp[i][j-1]}  s[i]!=t[j];

对于四维的：

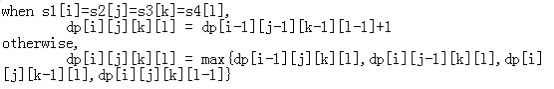
用一个DP来做就可以得到50pts了：

然鹅我……写炸了。

#include<bits/stdc++.h>

using namespace std;

int s[],t[],sr[],tr[];
int len_s,len_t,max1,max2;
int dp[][][][];
char s1[],t1[];

void scl(){
    for(int i=;i<len_s;i++){
        sr[len_s-i]=s1[i];
        s[i+]=s1[i];
    }
    for(int i=;i<len_t;i++){
        tr[len_t-i]=t1[i];
        t[i+]=t1[i];
    }
}

int main(){
    scanf("%s",s1);
    scanf("%s",t1);
    len_s=strlen(s1);
    len_t=strlen(t1);
    scl();
    for(int i=;i<=len_s;i++){
        for(int j=;j<=len_t;j++){
            for(int k=;k<=len_s;k++){
                for(int l=;l<=len_t;l++){
                    if(s[i]==sr[k]&&s[i]==t[j]&&s[i]==tr[l]&&sr[k]==t[j]&&sr[k]==tr[l]&&t[j]==tr[l])
//注意这里不能略写为s[i]==t[j]==sr[k]==tr[l]{
                    dp[i][j][k][l]=dp[i-][j-][k-][l-]+;
                    }
                    else {
                        max1=max(dp[i-][j][k][l],dp[i][j-][k][l]);
                        max2=max(dp[i][j][k-][l],dp[i][j][k][l-]);
                        dp[i][j][k][l]=max(max1,max2);
                    }
                }
            }
        }
    }
    cout<<dp[len_s][len_t][len_s][len_t]<<endl;
}

100pts：

暴力：一位一位的遍历，O（n*2^m）

显然很慢啊qwq；

加速？？？

维护一个26*n的数组，记录距离某个位置最近的某个字母（26个字母）在哪儿；

不会写qwq自闭

Problem3：

直接讲100pts的贪心：

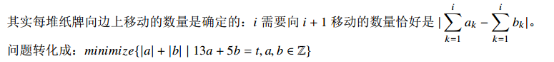
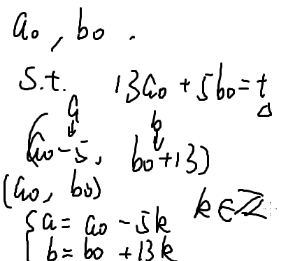
这个题的原理忘记为啥了？？？

即解一个二元一次方程组13a+5b=t。

所以我们分别枚举a，b找到最小的t；

复杂度O（30n）