搜索练习题——FBI树

目录：

·题目描述

·知识拓展

·题目分析

·思路分析

·代码实现

·总结

---

·题目描述：

（洛谷P1087 FBI树）

　　我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为B串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。

　　FBI树是一种二叉树，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2^N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下：

　　1) T的根结点为R，其类型与串S的类型相同；

　　2) 若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1​和S2​；由左子串S1​构造R的左子树T1​，由右子串S2​构造R的右子树T2​。

　　现在给定一个长度为2^N的“01”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历序列。

·知识拓展：

　　关于遍历的顺序：

　　（1）先序遍历：

　　　　

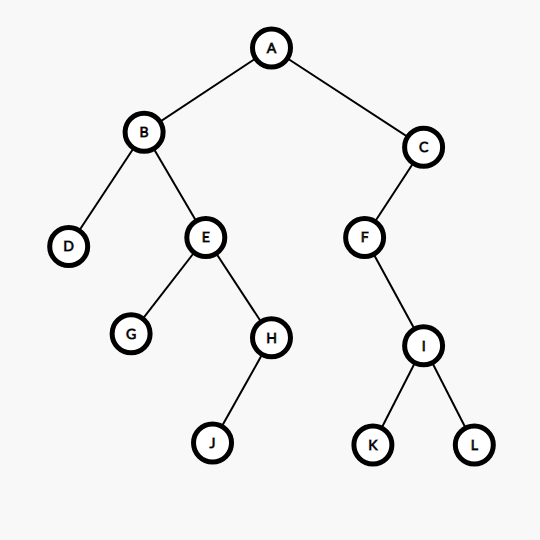
　　　　如图，这是一个二叉树，A为根结点。这张图如果用先序遍历表示的话，应为ABDEGHJCFIKL。总的来说，先序遍历的遍历方式为先根后左再右，简记为：根左右

　　（2）中序遍历：

　　　　

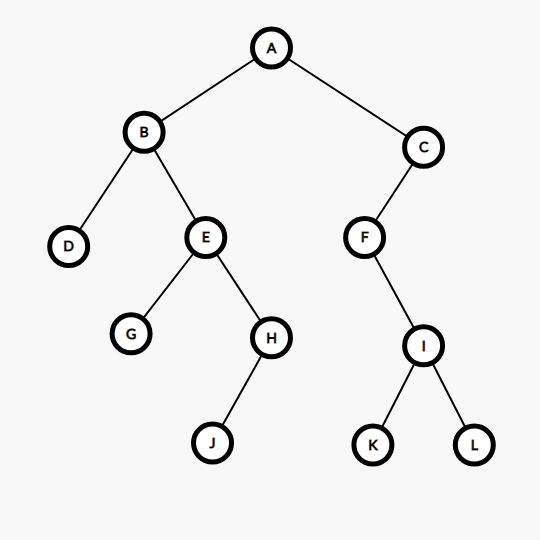
　　　　如图，还是这个二叉树，但是这张图如果用中序遍历表示的话，应为DBGEJHAFIKLC。不难看出，后序遍历的遍历方式为先左后根再右，简记为：左根右

　　（3）后序遍历：

　　　　

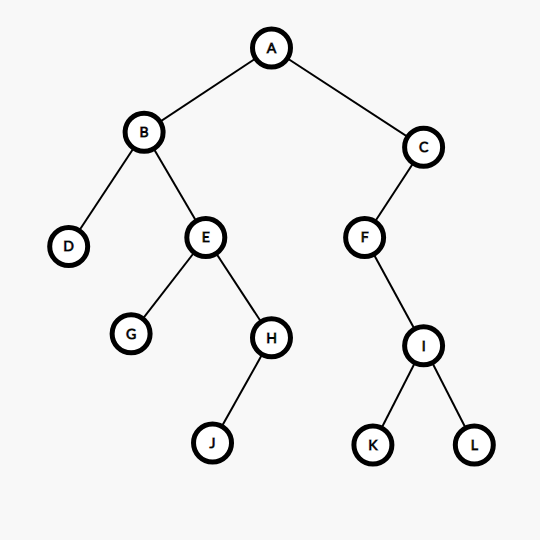
　　　　又是这张图，还是这个二叉树，用后序遍历表示这张图的话，应为DGJHEBKLIFCA。与上面的两种遍历方式相比较，可知，后序遍历的遍历方式为先左后右再根，简记为：左右根

·题目分析：

　　刚拿到这道题时，我没有仔细读题，只是将样例中的字符串写成了树，然后又按照后序遍历将这个字符串重新排列，将排列之后的字符串两个一组判断是F、B或I，但是这明显是错的。

　　本题的意思是将字符串写成树后，对每一个结点先进行判断F、B或I，然后按照后序遍历输出，没有对字符串长度的限制，不能两个一组进行判断

·思路分析：

　　对于这道题，我们可以采用边建树边输出的方法，结合深搜（其实就是一个大大的暴力），就可以得到这个题目的大致思路：

　　我们可以设一个dfs(l,r)函数，这个函数表示从l到r的字符串建树（并且输出F、B、I）

　　如果r-l>1，就将这个函数变为dfs(l,mid)和dfs(mid+1,r)，其中mid为l和r的中点，就是(l+r)/2

　　如果r-l=1，这个函数就递归到了尽头，则需要按照后序遍历的方式将F、B、I输出

·代码实现：

　　好了，talk is cheap，show me the code

 #include<iostream>
 #include<string>
 using namespace std;
 int n;
 string s;
 void dfs(int l,int r){
     if(l==r){
         if(s[l]=='')cout<<'B';
         if(s[l]=='')cout<<'I';
         return ;
     }
     int mid=(l+r)/;
     dfs(l,mid);
     dfs(mid+,r);//后序遍历
     bool B=true;//全是0
     bool I=true;//全是1
     for(int i=l;i<=r;i++){
         if(s[i]=='')B=false;//有1
         if(s[i]=='')I=false;//有0
     }
     if(B)cout<<'B';
     else if(I)cout<<'I';
     else cout<<'F';
 }
 int main(){
     cin>>n>>s;//用cin会好一点TwT
     dfs(,(<<n)-);//0~2^n-1
 }

　　

·总结：

　　这道题属于典型的“挂羊头卖狗肉”问题，题目名称和题目中的各个方面都是跟树相关，但是这个题目的解决方法却与树并没有太大的关系（虽然也用到了树的知识）。虽然自己图论学的不够好，但也不能因为题目中的暗示放弃了解题的机会啊！