剑指offer--day10

1.1 题目：二叉搜索树的后序遍历序列：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

1.2 思路：

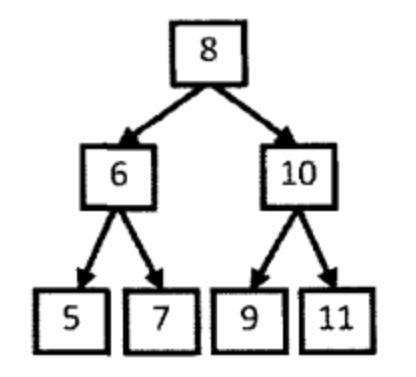
　　以{5,7,6,9,11,10,8}为例，后序遍历结果的最后一个数字8就是根结点的值。在这个数组中，前3个数字5、7和6都比8小，是值为8的结点的左子树结点；后3个数字9、11和10都比8大，是值为8的结点的右子树结点。

　　我们接下来用同样的方法确定与数组每一部分对应的子树的结构。这其实就是一个递归的过程。对于序列5、7、6，最后一个数字6是左子树的根结点的值。数字5比6小，是值为6的结点的左子结点，而7则是它的右子结点。同样，在序列9、11、10中，最后一个数字10是右子树的根结点，数字9比10小，是值为10的结点的左子结点，而11则是它的右子结点。

　　我们使用递归的方法，先判断数组的左子树和右子树的位置，然后再判断左子树、右子树是不是二叉搜索树。

1.3 代码：

 # -*- coding:utf-8 -*-
 class Solution:
     def VerifySquenceOfBST(self, sequence):
         # write code here
         length = len(sequence)
         if length == 0:
             return False
         if length == 1:
             return True
         root = sequence[-1]
         i = 0
         while sequence[i] < root:
             i =i + 1
         for j in range(i, length-1):
             if sequence[j] < root:
                 return False
         left_s = sequence[:i]
         right_s = sequence[i:length - 1]
         left, right = True, True
         if len(left_s) > 0:
             left1 = self.VerifySquenceOfBST(left_s)
         if len(right_s) > 0:
             right1 = self.VerifySquenceOfBST(right_s)
         return left and right

2.1 题目：二叉树和为某一值的路径：输入一颗二叉树的根节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)

2.2 思路：

　　深度优先搜索。使用前序遍历，使用两个全局变量result和tmp，result来存放最终结果，tmp用来存放临时结果。

　　每次遍历，我们先把root的值压入tmp，然后判断当前root是否同时满足：

• 与给定数值相减为0；
• 左子树为空；
• 右子树为空。

　　如果满足条件，就将tmp压入result中，否则，依次遍历左右子树。需要注意的是，遍历左右子树的时候，全局变量tmp是不清空的，直到到了根结点才请空tmp。

2.3 代码：

 # -*- coding:utf-8 -*-
 # class TreeNode:
 #     def __init__(self, x):
 #         self.val = x
 #         self.left = None
 #         self.right = None
 class Solution:
     # 返回二维列表，内部每个列表表示找到的路径
     def FindPath(self, root, expectNumber):
         # write code here
         if not root:
             return []
         if not root.left and not root.right and expectNumber == root.val:
             return [[root.val]]
         res = []
         left = self.FindPath(root.left, expectNumber - root.val)
         right = self.FindPath(root.right, expectNumber - root.val)
         for i in left + right:
             res.append([root.val] + i)
         return res