NOIP2011提高组 Day1 T3 Mayan游戏

题目描述

Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个7行×5列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1 、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图6到图7）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图1 和图2）；

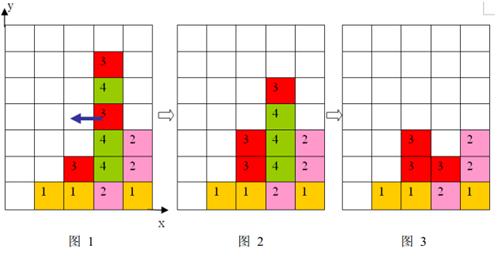
2 、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1 到图3）。

注意：

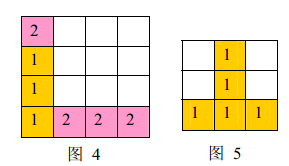
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图4，三个颜色为1的方块和三个颜色为 2的方块会同时被消除，最后剩下一个颜色为2的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5 所示的情形，5 个方块会同时被消除）。

3 、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0 ），将位于（3, 3 ）的方块向左移动之后，游戏界面从图 1 变成图 2 所示的状态，此时在一竖列上有连续三块颜色为4 的方块，满足消除条件，消除连续3 块颜色为4 的方块后，上方的颜色为3 的方块掉落，形成图 3 所示的局面。

输入输出格式

输入格式

共 6 行。

第一行为一个正整数n，表示要求游戏通关的步数。

接下来的5行，描述7×5 的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个0结束，自下向上表示每竖列方块的颜色编号（颜色不多于10种，从1开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式

如果有解决方案，输出n行，每行包含3个整数x,y,g表示一次移动，每两个整数之间用一个空格隔开，其中(x,y)表示要移动的方块的坐标，g 表示移动的方向，1表示向右移动，−1表示向左移动。注意：多组解时，按照x为第一关健字，y为第二关健字，1优先于−1，给出一组字典序最小的解。游戏界面左下角的坐标为(0,0)。

如果没有解决方案，输出一行，包含一个整数−1。

样例输入输出

样例输入

3

1 0

2 1 0

2 3 4 0

3 1 0

2 4 3 4 0

样例输出

2 1 1

3 1 1

3 0 1

说明

【输入输出样例解释】

按箭头方向的顺序分别为图6到图11

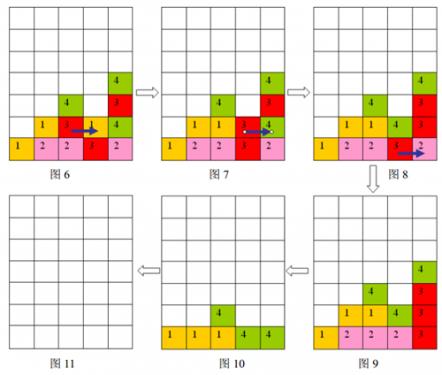
样例输入的游戏局面如上面第一个图片所示，依次移动的三步是：(2,1)处的方格向右移动，(3,1)处的方格向右移动，(3,0)处的方格向右移动，最后可以将棋盘上所有方块消除。

【数据范围】

对于30%的数据，初始棋盘上的方块都在棋盘的最下面一行；

对于100%的数据，0<n≤5。

解析

其实这是一道暴搜+剪枝的题目。我们只要按照题目的要求逐步去做就行了。

由于题目说界面的左下角为坐标(0,0)，我们就把整个格子顺时针旋转90度，使其与二位数组的存储规律相符。这样方块下坠就变成了纵坐标的改变，交换就变成了横坐标的改变。然后开始搜索。对于每一个方块，枚举其向左或向右移动，如果其移动方向上有方块就交换，否则就进行下坠操作（交换的两列都要下坠）。然后按照题目要求模拟消去、下坠、消去......的过程。题目要求字典序最小，那么我们优先枚举向右方向交换，这样第一次完成时的方案一定是字典序最小的。

这题的剪枝其实也还比较好想。用了贪心的思想，如果一个方块移动后，不会有任何一个方块（包括自身）与颜色相同的方块相连接，那么这次移动就是无意义的，可以舍去。至此，这道题目就解决了。

#include <iostream>
#include <cstdio>
using namespace std;
int a[10][10],i,n,px[10],py[10],pz[10];
bool e;
bool judge()
{
	for(int i=0;i<5;i++){
		for(int j=0;j<7;j++){
			if(a[i][j]!=0) return false;
		}
	}
	return true;
}
void doit()
{
	while(1){
		bool e=false,vis[10][10]={0};
		for(int i=0;i<5;i++){
			for(int j=0;j<7;j++){
				bool flag=false;
				if(a[i][j]!=0){
					if(i+1<5&&i-1>=0&&a[i-1][j]==a[i][j]&&a[i][j]==a[i+1][j]){
						flag=true;
						vis[i-1][j]=vis[i+1][j]=1;
					}
					if(j+1<7&&j-1>=0&&a[i][j-1]==a[i][j]&&a[i][j]==a[i][j+1]){
						flag=true;
						vis[i][j-1]=vis[i][j+1]=1;
					}
					if(flag){
						vis[i][j]=1;
						e=true;
					}
				}
			}
		}
		if(!e) break;
		for(int i=0;i<5;i++){
			for(int j=0;j<7;j++){
				if(vis[i][j]==1) a[i][j]=0;
			}
		}
		for(int i=0;i<5;i++){
			for(int j=1;j<7;j++){
				int x=i,y=j;
				if(a[x][y]==0) continue;
				while(y>0&&a[x][y-1]==0){
					swap(a[x][y-1],a[x][y]);
					y--;
				}
			}
		}
	}
}
void change(int b[10][10])
{
	for(int i=0;i<5;i++){
		for(int j=0;j<7;j++) a[i][j]=b[i][j];
	}
}
bool cut(int x,int y,int z)
{
	int p=0;
	while(a[x+z][p]!=0) p++;
	p--;
	if(a[x+z][y]==0){
		if(a[x][y+1]==a[x][y-1]) return 0;
		if(a[x+z-1][p+1]==a[x][y]||a[x+z+1][p+1]==a[x][y]) return 0;
		if(a[x+z][p]!=a[x][y]) return 1;
	}
	else if(a[x][y]==a[x+z][y+1]||a[x][y]==a[x+z][y-1]||a[x+z][y]==a[x][y+1]||a[x+z][y]==a[x][y-1]) return 0;
	else if(a[x+2*z][y]==a[x][y]||a[x-z][y]==a[x+z][y]) return 0;
	return 1;
}
void dfs(int num)
{
	if(e) return;
	if(num==n+1){
		if(judge()) e=true;
		return;
	}
	int b[10][10]={0};
	for(int i=0;i<5;i++){
		for(int j=0;j<7;j++) b[i][j]=a[i][j];
	}
	for(int i=0;i<5;i++){
		for(int j=0;j<7;j++){
			if(a[i][j]!=0){
				for(int k=1;k>=-1;k-=2){
					if(i+k<0||i+k>4||cut(i,j,k)) continue;
					int x=i,y=j;
					swap(a[x+k][y],a[x][y]);
					if(a[x][y]==0){
						int l=y+1;
						while(a[x][l]!=0){
							swap(a[x][l-1],a[x][l]);
							l++;
						}
					}
					x+=k;
					while(y>0&&a[x][y-1]==0){
						swap(a[x][y-1],a[x][y]);
						y--;
					}
					doit();
					px[num]=i;
					py[num]=j;
					pz[num]=k;
					dfs(num+1);
					if(e) return;
					change(b);
				}
			}
		}
	}
}
int main()
{
	cin>>n;
	for(i=0;i<5;i++){
		int x=1,cnt=0;
		cin>>x;
		while(x!=0){
			a[i][cnt++]=x;
			cin>>x;
		}
	}
	dfs(1);
	if(e){
		for(i=1;i<=n;i++) cout<<px[i]<<' '<<py[i]<<' '<<pz[i]<<endl;
	}
	else cout<<"-1"<<endl;
	return 0;
}

可能剪枝部分有点乱......