tensorflow白话篇

　　接触机器学习也有相当长的时间了，对各种学习算法都有了一定的了解，一直都不愿意写博客(借口是没时间啊)，最近准备学习深度学习框架tensorflow，决定还是应该把自己的学习一步一步的记下来，方便后期的规划。当然，学习一个新东西，第一步就是搭建一个平台，这个网上很多相关博客，不过，还是会遇到很多坑的，坑咋们不怕，趟过就好了。下面就以一个逻辑回归拟合二维数据为例来入门介绍吧。(参考书：深度学习之Tensorflow入门原理与进阶实践)

　　学习都是有一定套路的，深度学习一般情况下：准备数据、搭建模型、迭代训练及使用模型。当然，Tensorflow开发也是有套路的：

　　　　　　（1）定义Tensorflow输入节点

　　　　　　（2）定义“学习参数”等变量

　　　　　　（3）定义“运算”(定义正向传播模型 、定义损失函数)

　　　　　　（4）优化函数、优化目标（反向传播）

　　　　　　（5）初始化所有变量

　　　　　　（6）迭代更新参数直至最优解

　　　　　　（7）测试模型

　　　　　　（8）使用模型

　　在tensorflow中，将中间节点及节点间的运算关系(OPS)定义在内部的一个“图”上，全通过一个“会话（session）”进行图中OPS的具体运算。“图”是静态的，无论做任何运算，它们只是将关系搭建在一起，并不会做任何运算；而“会话”是动态的，只有启动会话后才会将数据流向图中，并按照图中的关系进行运算，并将最终的结果从图中流出。构建一个完整的图一般需要定义3种变量：输入结点(网络的入口)、学习参数(连接各个节点的路径)、模型中的节点。在实际训练中，通过动态的会话将图中的各个节点按照静态的规则运算起来，每一次的迭代都会对图中的学习参数进行更新调整，通过一定次数的迭代运算之后，最终所形成的图便是所需要的“模型”。而在会话中，任何一个节点都可以通过会话的run函数进行计算，得到该节点的真实数据。

　　模型内部的数据有正向和反向：正向，是数据从输入开始，依次进行个节点定义的运算，一直运算到输出，是模型最基本的数据流向，在模型的训练、测试、使用的场景中都会用到的。反向，只有在训练场景下才会用到，反项链式求导的方法，即先从正向的最后一个节点开始，计算此时结果值与真实值的误差，形成一个关于学习参数表示误差的方程，然后，对方程中的每个参数求导，得到其梯度修正值，同时反向推出上一层的误差，这样就将该层节点的误差按照正向的相反方向传到上一层，并接着计算上一层的修正值，如此反复下去进行传播，直到传到正向的第一个节点。

　　1、准备数据　　

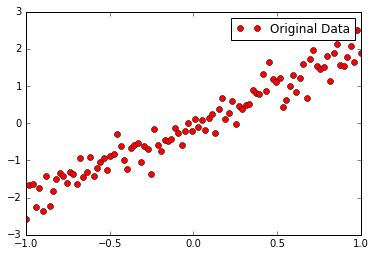
　　　　这里采用y=2x直线为主体，加入一些干扰噪声　　　　　

"""准备数据"""
train_X= np.linspace(-1,1,100)
train_Y= 2*train_X + np.random.randn(*train_X.shape)*0.3
plt.plot(train_X,train_Y,'ro',label="Original Data")
plt.legend()
plt.show()

　　　　　　　　　　　　　　　　　　　　　　　　

　　2、搭建模型

　　　　模型的搭建分两个方向:正向与反向

　　　　（1）正向搭建模型

　　　　　　神经网络大多是由多个神经元组成的，此处为了简单，采用单个神经元的网络模型。

　　　　　　

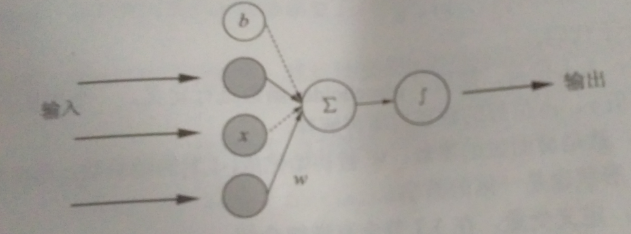
　　　　　　计算公式为：z=w*xT + b （其中，w是矩阵，xT是矩阵x的转置）w={w1,w2,...wi} xT={x1,x2.....xi}   i=1,2,....n  z表示输出结果，x为输入数据，w为权重，b为偏执值。

　　　　　　模型每次的"学习"过程本质上就是调整w,b的值，以获得更适合的值。

"""建立模型"""
 
#占位符
X=tf.placeholder("float")
Y=tf.placeholder("float")
#模型参数
W=tf.Variable(tf.random_normal([1]),name="weight")
b=tf.Variable(tf.zeros([1]),name="bias")
#前向
z=tf.multiply(X,W)+b

　　　　（2）反向搭建模型

　　　　　　在神经网络的训练过程中数据流向是有两个方向的，即先通过正向生成一个值，然后对比其与实际值的差距，再通过反向过程将里面的参数进行调整，接着再次正向生成预测值并与真实值进行对比，这样循环下去，直到将参数调整到合适值为止。

 #生成值与真实值的平方差
 cost= tf.reduce_mean(tf.square(Y-z))
 #学习率
 learning_rate= 0.01
 #梯度下降
 optimizer= tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

　　　　学习率代表调整参数的速度，这个值越大，表明调整的速度越大，相应的精确度越低，值越小，表明调整的精度越高，但学习速度越慢。GradientDescentOptimizer函数是一个封装好的梯度下降算法。

　　3、迭代训练模型

　　　　在tensorflow中，任务是通过Session来进行的，通过sess.run()来进行网络节点的运算，通过feed机制将真实数据加载到占位符对应的位置。

"""训练模型"""
init= tf.global_variables_initializer()
training_epochs=20
display_step=2
 
with tf.Session() as sess:
    sess.run(init)
    plotdata={"batchsize":[], "loss":[]}
 
    def moving_average(a, w=10):
        if len(a)<w:
            return a[:]
        return [val if idx <w else sum(a[(idx-w):idx])/w  for idx, val in enumerate(a)]
 
    for epoch in range(training_epochs):
        for (x,y) in zip(train_X, train_Y):
            sess.run(optimizer, feed_dict={X: x, Y:y })
 
        if epoch % display_step == 0:
            loss = sess.run(cost, feed_dict={ X: train_X, Y: train_Y })
            print ("Epoch:", epoch+1, " cost=", loss, "W=", sess.run(W), " b=",sess.run(b))
            if not (loss == "NA"):
                plotdata["batchsize"].append(epoch)
                plotdata["loss"].append(loss)
 
    print( "Finished.")
    print( "cost=", sess.run(cost, feed_dict={ X:train_X, Y:train_Y }), "W=", sess.run(W), "b=", sess.run(b))
 
    """训练模型可视化"""
    plt.plot(train_X, train_Y, "ro", label="Original Data")
    plt.plot(train_X, sess.run(W)*train_X +sess.run(b), label="FittedLine")
    plt.legend()
    plt.show()
 
    plotdata["avgloss"]= moving_average(plotdata["loss"])
    plt.figure(1)
    plt.subplot(211)
    plt.plot(plotdata["batchsize"], plotdata["avgloss"], "b--")
    plt.xlabel("Minibatch number")
    plt.ylabel("Loss")
    plt.title("Minibatch run vs.Training loss")
 
    plt.show()

结果：

Epoch: 1 cost= 0.9754149 W= [0.58673507] b= [0.4007497]
Epoch: 3 cost= 0.15794739 W= [1.648151] b= [0.11324686]
Epoch: 5 cost= 0.09357372 W= [1.9356339] b= [0.00494289]
Epoch: 7 cost= 0.08987887 W= [2.0101867] b= [-0.02363242]
Epoch: 9 cost= 0.08980431 W= [2.029468] b= [-0.03103093]
Epoch: 11 cost= 0.089843966 W= [2.0344524] b= [-0.03294369]
Epoch: 13 cost= 0.08985817 W= [2.0357416] b= [-0.03343845]
Epoch: 15 cost= 0.08986214 W= [2.0360765] b= [-0.03356693]
Epoch: 17 cost= 0.08986315 W= [2.0361621] b= [-0.03359992]
Epoch: 19 cost= 0.08986344 W= [2.0361862] b= [-0.03360903]
Finished.
cost= 0.0898635 W= [2.0361903] b= [-0.03361049]

　　       

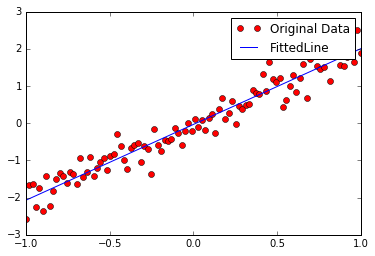
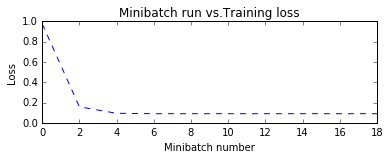
　　　可以清楚看到，cost的值在不断变小，w和b的值也在不断地调整。最后，趋于得到一条回归直线。

　　4、使用模型

　　　　模型训练郝红阳，使用起来就简单了

　　　　如：print("x=2,z=",sess.run(z, feed_dict={X:2 }))即可。

　　tensorflow中定义输入节点的方法：

　　　　　　（1）、通过占位符定义(一般情况下使用)如：

　　　　　　　　　　X=tf.placeholder("float")

　　　　　　　　　　Y=tf.placeholder("float")

　　　　　　（2）、通过字典类型定义(一般用于输入比较多的情况下)如：

　　　　　　　　inputdict = {

　　　　　　　　　　　　　　'x' : tf.placeholder("float),

　　　　　　　　　　　　　　'y' : tf.placeholder("float")

　　　　　　　　　　　　　}

　　　　　　(3)直接定义*(一般很少用)：将定义好的变量直接放到OP节点中参与输入运算进行训练。

　　完整代码：　

# -*- coding: utf-8 -*-
"""
Spyder Editor
 
@Author:wustczx
"""
 
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
 
"""准备数据"""
train_X= np.linspace(-1,1,100)
train_Y= 2*train_X + np.random.randn(*train_X.shape)*0.3
plt.plot(train_X,train_Y,'ro',label="Original Data")
plt.legend()
plt.show()
 
"""建立模型"""
X=tf.placeholder("float")
Y=tf.placeholder("float")
 
W=tf.Variable(tf.random_normal([1]),name="weight")
b=tf.Variable(tf.zeros([1]),name="bias")
 
z=tf.multiply(X,W)+b
 
#生成值与真实值的平方差
cost= tf.reduce_mean(tf.square(Y-z))
#学习率
learning_rate= 0.01
#梯度下降
optimizer= tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
 
"""训练模型"""
init= tf.global_variables_initializer()
training_epochs=20
display_step=2
 
with tf.Session() as sess:
    sess.run(init)
    plotdata={"batchsize":[], "loss":[]}
 
    def moving_average(a, w=10):
        if len(a)<w:
            return a[:]
        return [val if idx <w else sum(a[(idx-w):idx])/w  for idx, val in enumerate(a)]
 
    for epoch in range(training_epochs):
        for (x,y) in zip(train_X, train_Y):
            sess.run(optimizer, feed_dict={X: x, Y:y })
 
        if epoch % display_step == 0:
            loss = sess.run(cost, feed_dict={ X: train_X, Y: train_Y })
            print ("Epoch:", epoch+1, " cost=", loss, "W=", sess.run(W), " b=",sess.run(b))
            if not (loss == "NA"):
                plotdata["batchsize"].append(epoch)
                plotdata["loss"].append(loss)
 
    print( "Finished.")
    print( "cost=", sess.run(cost, feed_dict={ X:train_X, Y:train_Y }), "W=", sess.run(W), "b=", sess.run(b))
 
    """训练模型可视化"""
    plt.plot(train_X, train_Y, "ro", label="Original Data")
    plt.plot(train_X, sess.run(W)*train_X +sess.run(b), label="FittedLine")
    plt.legend()
    plt.show()
 
    plotdata["avgloss"]= moving_average(plotdata["loss"])
    plt.figure(1)
    plt.subplot(211)
    plt.plot(plotdata["batchsize"], plotdata["avgloss"], "b--")
    plt.xlabel("Minibatch number")
    plt.ylabel("Loss")
    plt.title("Minibatch run vs.Training loss")
 
    plt.show()