算法总结—深度优先搜索DFS

深度优先搜索（DFS）

往往利用递归函数实现（隐式地使用栈）。

深度优先从最开始的状态出发，遍历所有可以到达的状态。由此可以对所有的状态进行操作，或列举出所有的状态。

1.poj2386 Lake Couting

题意：八连通被认为连接在一起，求总共有多少个水洼？

Sample Input：

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

Sample Output

3

思路：从任意W开始，一次DFS把连通的.全部变为W,遍历图直到没有.为止，进行DFS次数即为水洼的个数。
代码：

 #include<iostream>
 using namespace std;
 int N, M;
 char pond[][]; //global variable
 void dfs(int i, int j){ // 注意参数设计，要不要返回值
     pond[i][j] = '.';
     for(int dx = -; dx <= ; ++dx){ //八连通遍历方式，四连通往往事先开好数组，见后续题目
         for(int dy = -; dy <= ; ++dy){
             int x = i + dx, y = j + dy;
             if(x >=  && x < N && y >=  && y < M && pond[x][y] == 'W'){
                 dfs(x,y);
             }
         }
     }
     return;
 }
 int main(){
     cin >> N >> M;
     for(int i = ; i < N; ++i){
         for(int j = ; j < M; ++j){
             cin >> pond[i][j];
         }
     }

     int count = ;
     for(int i = ; i < N; ++i){
         for(int j = ; j < M; ++j){
             if(pond[i][j] == 'W'){
                 dfs(i,j);
                 count ++;
             }
         }
     }
     cout << count << endl;
 }

2.poj1979 Red and Black

题意：@表示起点，可以上下左右四方向走，"."为黑色，可以走，“#”为红色，不可以走，问可以到达多少个黑色位置？

Sample Input

6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
11 6
..#..#..#..
..#..#..#..
..#..#..###
..#..#..#@.
..#..#..#..
..#..#..#..
7 7
..#.#..
..#.#..
###.###
...@...
###.###
..#.#..
..#.#..
0 0

Sample Output

45
59
6
13

思路：从起点处DFS遍历即可，当前点为“.”则将其改为“#”，result++,并以该点出发继续遍历。
代码：

 #include<iostream>
 using namespace std;
 char rect[][];
 int result = ;  //全局的result
 int dx[] = {-,,,};  //四连通处理方法
 int dy[] = {,,-,};
 int W = , H = ;
 void dfs(int sx, int sy){
     rect[sx][sy] = '#';
     result++;
     for(int i = ; i < ; ++i){
         int x = sx + dx[i], y = sy + dy[i];
         if(x >=  && x < H && y >=  && y < W && rect[x][y] == '.'){
             dfs(x,y);
         }
     }
     return ;
 }
 int main(){
     while(W !=  && H != ){
         cin >> W >> H;
         if(W ==  && H == ){
             return ;
         }
         int sx, sy;
         for(int i = ; i < H; ++i){
             for(int j = ; j < W; ++j){
                 cin >> rect[i][j];
                 if(rect[i][j] == '@'){
                     sx = i;
                     sy = j;
                 }
             }
         }
         dfs(sx, sy);
         cout << result << endl;
         result = ;
     }
     return ;
 } 

3.aoj0118 Property Distribution

题意： 苹果是@，梨是#， 蜜柑是*。 四连通且相同品种在一个区域。计算每组数据区域的个数。

Sample Input：

10 10
####*****@
@#@@@@#*#*
@##***@@@*
#****#*@**
##@*#@@*##
*@@@@*@@@#
***#@*@##*
*@@@*@@##@
*@*#*@##**
@****#@@#@
0 0

Output for the Sample Input

33

思路：类似第一题的池塘数个数的思路，DFS遍历，将遍历完毕的节点改为不同于上述三种标志的第四种标志，如“X”,
     并且在DFS函数中加入标志参数用于判断同类水果区域，一次DFS，result++，当所有标志为X时，遍历结束。
代码：

 #include<iostream>
 using namespace std;
 char garden[][];
 int H = , W = ;
 int result = ;
 int dx[] = {-,,,};
 int dy[] = {,,-,};
 void dfs(int sx, int sy,char c){ //加入char判断是否同一类
     garden[sx][sy] = 'x';
     for(int i = ; i < ;++i){
         int x = sx + dx[i], y = sy + dy[i];
         if(x >=  && x < H && y >=  && y < W && garden[x][y] == c){
             dfs(x,y,c);
         }
     }
     return;
 }
 int main(){
     while(H !=  && W != ){
         cin >> H >> W;
         if(H ==  && W == ){
             return ;
         }
         for(int i = ; i < H; ++i){
             for(int j = ; j < W; ++j){
                 cin >> garden[i][j];
             }
         }
         for(int i = ; i < H; ++i){
             for(int j = ; j < W; ++j){
                 if(garden[i][j] != 'x'){
                     dfs(i,j,garden[i][j]);
                     result++;
                 }
             }
         }
         cout << result << endl;
         result = ;
     }
 }

4.aoj0033 Ball
题意：A管进球，B,C管出球，给定如球顺序，判断能否移动挡板，使得B,C出球顺序均为从下往上标号递增。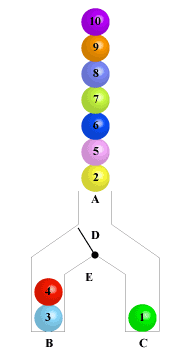

Sample Input

2
3 1 4 2 5 6 7 8 9 10
10 9 8 7 6 5 4 3 2 1

Output for the Sample Input

YES
NO

思路：DFS遍历，一个参数记录当前到第几个球，另外两个记录当前B,C顶端球得数值，以便于比较。
代码：

 #include<iostream>
 using namespace std;
 int A[];
 bool dfs(int start, int topB, int topC){  //有返回值的DFS
     if(start == ){  //最后一个球啦
         if(A[start] > topB || A[start] > topC){
             return true;
         }
         else{
             return false;
         }
     }
     bool b1 = false, b2 = false;
     if(A[start] > topB){  //B可以放，放进去试
         b1 = dfs(start+, A[start], topC);
     }
     if(A[start] > topC){ //C可以放，放进去试
         b2 = dfs(start+,topB,A[start]);
     }
     return (b1 || b2 );   //B,C都不可以放的时候，返回false，否则true
 }
 int main(){
     int N;
     cin >> N;
     for(int i = ; i < N; ++i){
         for(int j = ; j < ; ++j){
             cin >> A[j];
         }
         bool result = dfs(,,);
         if(result == true){
             cout << "YES" << endl;
         }
         else{
             cout << "NO" <<endl;
         }
     }
     return ;
 }

 5. poj3009 Curling 2.0

题意：

可以沿上下左右走到障碍物，碰到障碍物后停下，障碍物消失，然后可以继续出发，出界算失败，超过十步算失败，问能否从S到G，

不能输出-1，能输出最少步数。(0路径，1障碍物，2起点，3终点)

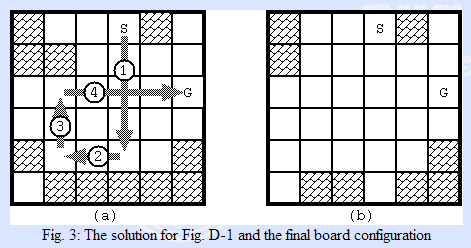
Sample Input

2 1
3 2
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
6 1
1 1 2 1 1 3
6 1
1 0 2 1 1 3
12 1
2 0 1 1 1 1 1 1 1 1 1 3
13 1
2 0 1 1 1 1 1 1 1 1 1 1 3
0 0

Sample Output

1
4
-1
4
10
-1

思路：这种走到底的题目也可以用DFS，设计成无返回值，到达3后比较当前值与已有最小值的大小。注意走到底的写法（while）

代码：

 #include<iostream>
 #include<cstring>
 #include<limits.h>
 using namespace std;
 int board[][];
 int W = , H = ;
 int dx[] = {-,,,};
 int dy[] = {,,-,};
 int sx, sy,minStep = INT_MAX;
 void dfs(int sx,int sy,int step){    //设计成无返回值，当board[i][j] == 3时比较当前 step+1 与最小的step并更新
     if(step >= ){     //剪枝
         return;
     }
     for(int i = ; i < ;++i){
         int x = sx + dx[i], y = sy + dy[i];
         if(x >=  && x < H && y >= && y < W && board[x][y] != ){
             while(x >=  && x < H && y >= && y < W && board[x][y] != ){ //走到底的判断
                 if(board[x][y] == ){
                     if(step +  < minStep){
                         minStep = step + ;
                         break;
                     }
                 }
                 x += dx[i];
                 y += dy[i];
                 if(board[x][y] == ){
                     board[x][y] = ;
                     dfs(x - dx[i], y - dy[i], step + );
                     board[x][y] = ;    // 恢复状态
                 }
             }
         }
     }
     return;
 }

 int main(){
     while(W !=  && H != ){
         cin >> W >> H;
         if(W ==  && H == ){
             return ;
         }
         memset(board,,sizeof(board));
         for(int i = ; i < H; ++i){
             for(int j = ; j < W; ++j){
                 cin >> board[i][j];
                 if(board[i][j] == ){
                     sx = i;
                     sy = j;
                 }
             }
         }
         dfs(sx,sy,);
         if(minStep == INT_MAX){
             cout << "-1" << endl;
         }
         else{
             cout << minStep << endl;
         }
         minStep = INT_MAX;
     }
     return ;
 }

6.poj1321 棋盘问题

题意：n*n矩阵形状的棋盘（“#”为可摆放棋盘区域，“.”为不可摆放空白区域），要摆放k个棋子，同行同列不能有两个，共多少种方案？

Sample Input

2 1
#.
.#
4 4
...#
..#.
.#..
#...
-1 -1

Sample Output

2
1

思路：DFS的思路，一行一行的确定摆放位置，开一个数组place[8]记录哪一列已经有摆放。
注意k如果小于N时，可以有某一行不摆放元素，所以代码24行 DFS(row+1,num) 必须添加。

代码：

 #include<iostream>
 #include<cstring>
 using namespace std;
 int N = ,K = ;
 char chess[][];
 int result = ;
 int placed[] = {};  //记录该列是否有摆放
 void dfs(int row,int num){
     if(num == K){   //摆放成功，方案数++
         result++;
         return;
     }
     if(row == N){
         return;
     }

     for(int i = ; i < N; ++i){
         if(chess[row][i] == '#' && placed[i] == ){
             placed[i] = ;
             dfs(row + , num + );
             placed[i] = ;
         }
     }
     dfs(row+,num);  //！容易忽略

 }
 int main(){
     while(N != - && K != -){
         cin >> N >> K;
         if(N == - && K == -){
             return ;
         }
         memset(chess,,sizeof(chess));
         memset(placed,,sizeof(placed));
         for(int i = ; i < N;++i){
             for(int j = ; j < N; ++j){
                 cin >> chess[i][j];
             }
         }
         dfs(,);
         cout << result << endl;
         result = ;
     }

 }