hihocoder 1049 后序遍历

#1049 : 后序遍历

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在参与过了美食节之后，小Hi和小Ho在别的地方又玩耍了一阵子，在这个过程中，小Ho得到了一个非常有意思的玩具——一棵由小球和木棍连接起来的二叉树！

小Ho对这棵二叉树爱不释手，于是给它的每一个节点都标记了一个标号——一个属于A..Z的大写字母，并且没有任意两个节点的标号是一样的。小Hi也瞅准了这个机会，重新巩固了一下小Ho关于二叉树遍历的基础知识~就这样，日子安稳的过了两天。

这天，小Ho正好在求解这棵二叉树的前序、中序和后序遍历的结果，但是却在求出前序遍历和中序遍历之后不小心把二叉树摔到了地上，小球和木棍等零件散落了一地！

小Ho损失了心爱的玩具，正要嚎啕大哭起来，所幸被小Hi发现了，劝说道：“别着急，这不是零件都还在么？拼起来不就是了？”

“可是我忘记了二叉树长什么样子了！”小Ho沮丧道。

“这个简单，你不是刚刚求出了这棵二叉树的前序和中序遍历的结果么，利用这两个信息就可以还原出整棵二叉树来哦！”

“这样么？！！”小Ho止住了泪水，问道：“那要怎么做呢？”

没错！小Ho在这一周遇到的问题便是：给出一棵二叉树的前序和中序遍历的结果，还原这棵二叉树并输出其后序遍历的结果。

输入

每个测试点（输入文件）有且仅有一组测试数据。

每组测试数据的第一行为一个由大写英文字母组成的字符串，表示该二叉树的前序遍历的结果。

每组测试数据的第二行为一个由大写英文字母组成的字符串，表示该二叉树的中序遍历的结果。

对于100%的数据，满足二叉树的节点数小于等于26。

输出

对于每组测试数据，输出一个由大写英文字母组成的字符串，表示还原出的二叉树的后序遍历的结果。

样例输入

AB
BA

样例输出

BA

提示：分而治之——化大为小，化小为无

“这可就要从头说起了，我们先找一棵二叉树作为例子吧！”小Hi在纸上画了画，递给了小Ho。

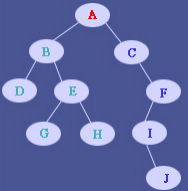
“不妨假设你的二叉树长成这个样子~”小Hi道。

“可是我的二叉树并不是长成这个样子啊！虽然我读书少，但是你不要骗我好不好！”小Ho一脸气愤道。

“我都说了是假设！是为了能让你明白如何通用的去解决这样的问题！”小Hi无奈道。

“好吧……你接着说。”小Ho算是认可了这个说法。

“那么对于这棵二叉树，你先来计算一下它的前序遍历和中序遍历的结果吧！”小Hi也是毫不含糊就开始下发任务。

“唔……前序遍历是ABDEGHCFIJ，中序遍历……我想想啊……是DBGEHACIJF！”小Ho并没有花费多长时间就给出了答案。

“你还记得前序遍历的递归定义么？”小Hi点了点头又继续问道。

“是‘根节点’+‘左子树的前序遍历’+‘右子树的前序遍历’！”小Ho毫不犹豫的答道：“而在这里体现出来就是‘A'+‘BDEGH’+‘CFIJ’”。

“那中序遍历呢？”小Hi继续问道。

“是‘左子树的中序遍历’+‘根节点’+‘右子树的中序遍历’！在这里也就是‘DBGEH’+‘A’+‘CIJF’。”小Ho这次花的时间更少了。

“还记得动态规划时候我们一般处理的方法么？我们这里也可以这样做哦，如果我们定义post_order(str1, str2)为一棵前序遍历的结果为str1，中序遍历的结果为str2的二叉树的后序遍历的结果的话，我们有没有办法把它化解成为子问题呢？”小Hi道。

“让我想想……”小Ho拿出纸笔开始演算起来：“如果我要求解post-order(str1, str2)的话，首先不难发现，根据‘前序遍历’str1=‘根节点’+‘左子树的前序遍历’+‘右子树的前序遍历’，我可以知道这棵二叉树的根节点root便是str1的第一个字符！”小Ho道。

“而我在知道了‘根节点’root之后，我便可以利用‘中序遍历’str2=‘左子树的中序遍历’+‘根节点’+‘右子树的中序遍历’，求解出‘左子树的中序遍历’str2L和‘右子树的中序遍历’str2R！”

“接下来，由于一棵子树的前序遍历和中序遍历的长度相同，那么仍然是根据‘前序遍历’str1=‘根节点’+‘左子树的前序遍历’+‘右子树的前序遍历’，我可以知道从str1的第2个字符开始的str2L.length()个字符便是‘左子树的前序遍历’str1L，而这之后的部分便是‘右子树的前序遍历’str1R！”小Ho说到这里，顿了顿，希望从小Hi处得到些反馈。

“没错！那你准备如何求解post_order(str1, str2)呢？”小Hi肯定道。

“这只要根据之前求出的结果，和‘后序遍历’=‘左子树的后序遍历’+‘右子树的后序遍历’+‘根节点’，便可以知道——post_order(str1, str2)=post_order(str1l, str2l)+post_order(str1r, str2r)+root这样一个式子来！而这个问题的规模——也就是二叉树的大小，是一直在缩小的，所以是能够这样不断的划分做下去的！也就是说我之后可以将当前根节点的左子树又拆分成为两个问题来解决，一直到当前节点是叶子节点了为止！然后慢慢的将这些答案拼成上层的问题的答案，而这个过程只需要使用递归完成就可以了！”

“听起来很容易的样子呢！那你要不要赶紧去实现了算法，算出你的宝贝二叉树长什么样呢？”小Hi满意的点了点头，随即笑着问道。

“那是自然！”

代码一：

 #include <iostream>
 #include <string>
 using namespace std;

 string PostOrder(string str1, string str2){
     int len = str1.length();
     if(len == )
         return "";
     char in = str1[];
     int i, j;
     string str = "", strl, strr, preorder_str_left = "", inorder_str_left = "", preorder_str_right = "", inorder_str_right = "";
     for(i = ; i < len; i++){
         if(str2[i] == in)
             break;
         else
             inorder_str_left += str2[i];//得到左子树的中序遍历串
     }

     for(j = ; j < i + ; j++)
         preorder_str_left += str1[j];//得到左子树的前序遍历串

     for(j = i+; j < len; j++)
         inorder_str_right += str2[j];//得到右子树的中序遍历串

     for(j = i+; j < len; j++)
         preorder_str_right += str1[j];//得到右子树的前序遍历串

     strl = PostOrder(preorder_str_left, inorder_str_left);
     strr = PostOrder(preorder_str_right, inorder_str_right);
     str = str + strl + strr + in;
     return str;
 }

 int main(){
     string preorder_str, inorder_str;
     cin >> preorder_str >> inorder_str;
     cout << PostOrder(preorder_str, inorder_str) << endl;
     return ;
 }

代码二：

 #include <iostream>
 #include <string>
 using namespace std;

 string PostOrder(const char *str1, const char *str2, int length){//length为树遍历串的长度
     if(length == )
         return "";
     string strl, strr, str;
     int index = ;
     char in = str1[];
     while(str2[index] != in) index++;//index为左子树遍历串的长度
     strl = PostOrder(str1+, str2, index);
     strr = PostOrder(str1+index+, str2+index+, length-index-);
     str = strl + strr + in;
     return str;
 }

 int main(){
     string preorder_str, inorder_str;
     cin >> preorder_str >> inorder_str;
     cout << PostOrder(preorder_str.c_str(), inorder_str.c_str(), preorder_str.length()) << endl;
     return ;
 }

c++中c_str()学习：

语法:
const char *c_str();
c_str()函数返回一个指向正规C字符串的指针, 内容与本string串相同.
这是为了与c语言兼容，在c语言中没有string类型，故必须通过string类对象的成员函数c_str()把string 对象转换成c中的字符串样式。
注意：一定要使用strcpy()函数 等来操作方法c_str()返回的指针
比如：最好不要这样:
char* c;
string s="1234";
c = s.c_str(); //c最后指向的内容是垃圾，因为s对象被析构，其内容被处理

应该这样用：
char c[20];
string s="1234";
strcpy(c,s.c_str());
这样才不会出错，c_str()返回的是一个临时指针，不能对其进行操作

再举个例子
c_str() 以 char* 形式传回 string 内含字符串
如果一个函数要求char*参数，可以使用c_str()方法：
string s = "Hello World!";
printf("%s", s.c_str()); //输出 "Hello World!"