Project Euler 78:Coin partitions

Coin partitions

Let p(n) represent the number of different ways in which n coins can be separated into piles. For example, five coins can separated into piles in exactly seven different ways, so p(5)=7.

OOOOO
OOOO O
OOO OO
OOO O O
OO OO O
OO O O O
O O O O O

Find the least value of n for which p(n) is divisible by one million.

---

硬币分拆

记p(n)是将n枚硬币分拆成堆的不同方式数。例如，五枚硬币有7种分拆成堆的不同方式，因此p(5)=7。

OOOOO
OOOO O
OOO OO
OOO O O
OO OO O
OO O O O
O O O O O

找出使p(n)能被一百万整除的最小n值。

思路:

求数的拆分有多少种

再判断是否能被一百万整除

参考资料:wiki ,PartitionFunctionP

法一:

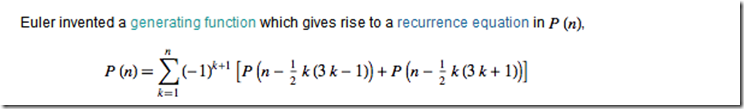
根据这个等式:

高能预警:

1.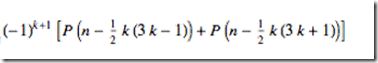  这里是两部分的和

2.当第一个不满足条件,即:n<k(3k-1)/2 时候，第二个一定不成立

3.第一个满足条件，第二个可能不满足条件，这里说的条件都是数组下标不能越界

4.满足条件的都要计算，只有当第一个不满足条件的时候才本次循环

5.前面的（-1）^(k+1)，要乘进去，展开计算，就是计算符合条件的数组

关键程序：

for(k=1;k<=n;k++){
                gk1 = k*(3*k-1)/2;
                gk2 = gk1+k;
                if(gk1>n) break;
                    plist.set(n,plist.get(n)+flag*plist.get(n-gk1));
                    if(gk2<=n){
                    plist.set(n,plist.get(n)+flag*plist.get(n-gk2));
                    }
                    plist.set(n,plist.get(n)%limit);
                    flag*=-1;
            }

这里由于我只是在上面看到的求解表达式，造成我搞了好久都没有搞出来，没文化正可怕

法二：

看到这里还没有出问题

看到这里，直接根据上面的表达式求解了，然而这里的k不是从1-n，这里我又理解错了，以为拿来用就好了

上面的方法不行，下面的方法也不行，真是浪费了好多时间的

下面程序中有一个求k的过程，这里才是真谛啊！！！

关键程序：

while(gk<=n){
                flag = (i%4>1)?-1:1;
                plist.set(n,plist.get(n)+flag*plist.get(n-gk));
                plist.set(n,plist.get(n)%limit);
                i++;
                int  k= (i%2==0)?i/2+1:-(i/2+1);
                gk = k*(3*k-1)/2;
            }

Java程序：

package Level3;

import java.util.ArrayList;

public class PE078{

    void run(){
        int limit = 1000000;
        partitions2(limit);
    }
    void partitions2(int limit){
        ArrayList<Integer> plist = new ArrayList<Integer>();
        plist.add(1);
        int n = 1;
        while(true){
            int gk1 =1;
            int gk2 =2;
            int k=1;
            plist.add(0);// 初始第n
            int flag = 1;
            for(k=1;k<=n;k++){
                gk1 = k*(3*k-1)/2;
                gk2 = gk1+k;
                if(gk1>n) break;
                    plist.set(n,plist.get(n)+flag*plist.get(n-gk1));
                    if(gk2<=n){
                    plist.set(n,plist.get(n)+flag*plist.get(n-gk2));
                    }
                    plist.set(n,plist.get(n)%limit);
                    flag*=-1;
            }
            if(plist.get(n)==0)
                break;
            n++;
        }
        System.out.println(n);
    }
//    55374
//    running time=0s784ms
    void partitions1(int limit){
        ArrayList<Integer> plist = new ArrayList<Integer>();
        plist.add(1);
        int n = 1;
        int flag;
        while(true){
            int gk = 1;
            int i = 0;
            plist.add(0);
            while(gk<=n){
                flag = (i%4>1)?-1:1;
                plist.set(n,plist.get(n)+flag*plist.get(n-gk));
                plist.set(n,plist.get(n)%limit);
                i++;
                int  k= (i%2==0)?i/2+1:-(i/2+1);
                gk = k*(3*k-1)/2;
            }

            if(plist.get(n)==0)
                break;
            n++;
        }
        System.out.println(n);
    }
//    55374
//    running time=1s155ms

    public static void main(String[] args){
        long t0 = System.currentTimeMillis();
        new PE078().run();
        long t1 = System.currentTimeMillis();
        long t = t1 - t0;
        System.out.println("running time="+t/1000+"s"+t%1000+"ms");

    }
}

法三：

又给出了求k的一种方式

关键程序：

while True:
            gk = k * (3 * k - 1) // 2
            i = n - gk
            if i < 0:
                break
            pt += (-1) ** (k * k + 1) * p[i]
            k = -1 * k if k > 0 else 1 - k
        p.append(pt)

python程序：

import time ;

def partitions(limit):
    p = [1, 1, 2]
    n = 2
    while True:
        n += 1
        pt = 0
        i = 0
        k = 1
        while True:
            gk = k * (3 * k - 1) // 2
            i = n - gk
            if i < 0:
                break
            pt += (-1) ** (k * k + 1) * p[i]
            k = -1 * k if k > 0 else 1 - k
        p.append(pt)
        if pt % limit == 0:
            print "n =", n, "\n"+"partition =", pt
            break

if __name__=='__main__':
    t0 = time.time()
    limit = 1000000
    partitions(limit)
    t1 = time.time()
    print "running time=",(t1-t0),"s"

# n = 55374
# running time= 21.3049998283 s

说明：只有第一种方法是我自己写的，其他是在论坛看到的，自己整理的