重修 Slope Trick（看这篇绝对够！）

Slope Trick 算法存在十余载了，但是我没有找到多少拍手叫好的讲解 blog，所以凭借本人粗拙的理解来写这篇文章。

本文除标明外所有图片均为本人手绘（若丑见谅），画图真的不容易啊 qwq（无耻求赞）。

Slope Trick 是啥？

凸代价函数DP优化。

具体哪种题目？

AcWing273. 分级

CF713C Sonya and Problem Wihtout a Legend

CF13C Sequence

P2893 [USACO08FEB]Making the Grade G

P4331 [BalticOI 2004]Sequence 数字序列

P4597 序列 sequence

P8118 Mystery

千万题目汇成一句话：

给定长度为 \(N(\le 10^6)\) 的序列 \(A\)，构造一个长度为 \(N\) 的非降序列 \(B\)，最小化 \(S=\sum\limits^N_{i=1}|A_i−B_i|\)，求出 \(S\) 的最小值和 \(B\) 的构造方案。

注意 Slope Trick 不止能够解决这个问题，这个题目只是便于举例而已。

暴力咋做？

就是 \(O(n^2)\) 的 DP。

设 \(f_{i,j}\) 表示 \(A\) 中第 \(i\) 个数变为 \(j\)，前 \(i\) 个数变为非降序列的最小代价，即

\[\min_{B_1\le B_2\le\dots\le B_i=j}\sum_{k=1}^{i}|A_k−B_k|
\]

则有递推式

\[f_{i,j}=|A_i-j|+\min_{k=minV}^{j} f_{i-1,k}
\]

其中 \(minV\) 指值域下界。

当然，为了后续的拓展，我们设

\[g_{i,j}=\min_{k=minV}^{j}f_{i,k}
\]

则递推式改成

\[f_{i,j}=|A_i-j|+g_{i-1,j}
\]

是不是非常美观？

过渡

在下一步之前，我们需要几个定义和引理。

引理 A

两个斜率分别为 \(a,b\) 的一次函数相加的斜率为 \(a+b\)。

定义 1

我们称这样的函数为美妙的函数：

• 函数连续。
• 函数由若干条一次函数（或常数函数）拼接而成（所以是分段函数），且一次函数的斜率为整数。
• 函数下凸，即若干条一次函数的斜率从左往右单调非减。

引理 B

任意两个美妙的函数相加还是美妙的函数。

定义 2

设一个连续函数 \(f(x)\) 的前缀最小函数 \(g(x)\) 为

\[g(x)=\min_{x'\le x}f(x')
\]

引理 C

一个美妙的函数的前缀最小函数还是美妙的函数，且最后一段（至 \(x\to\infty\)）为常数函数。

咋拓展到 Slope Trick？（正题）

先回忆一下递推式

\[f_{i,j}=|A_i-j|+g_{i-1,j}
\]

我们设 \(F_i(x)\) 函数

\[F_i(x)=f_{i,x}
\]

类似地

\[G_i(x)=g_{i,x}
\]

最后设

\[H_i(x)=|x-A_i|
\]

我们再次改写递推式

\[F_i(x)=H_i(x)+G_{i-1}(x)
\]

简洁美观！（请牢记这个公式）

由数学归纳法得到 \(F,G,H\) 都是美妙的函数。

我们维护 \(S_1,S_2,\dots,S_c\) 为 \(G\) 函数的转折点。

来几张图演示一下。

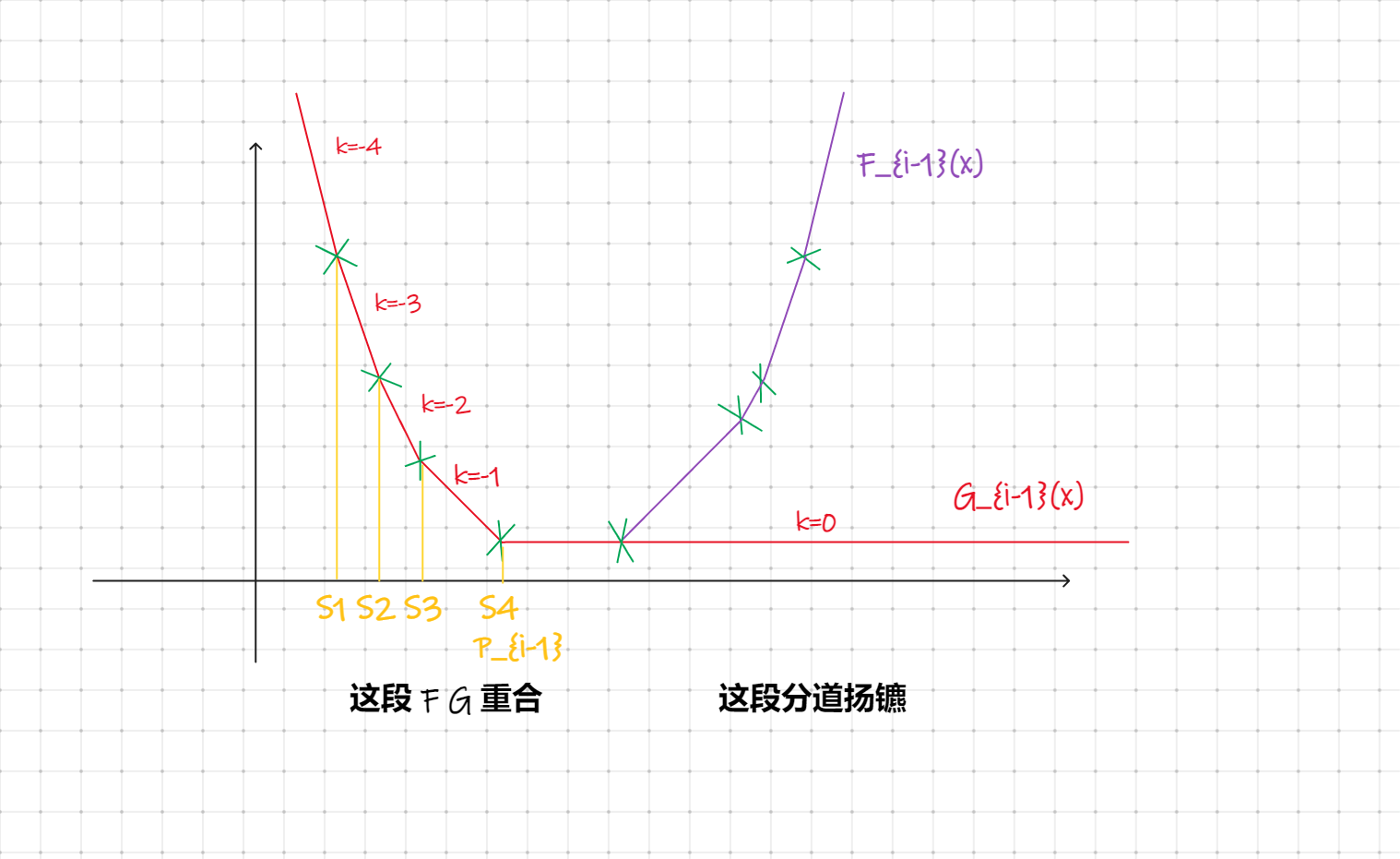
设这个 \(G_i\) 从一次函数到常数函数的转折点为 \(P_i\)。

值得注意的是，若一个转折点左边斜率 \(>\) 右边斜率 \(+1\)，则这个点是要再重复 \((\) 左边斜率 \(-\) 右边斜率 \(-1)\) 次的，即：

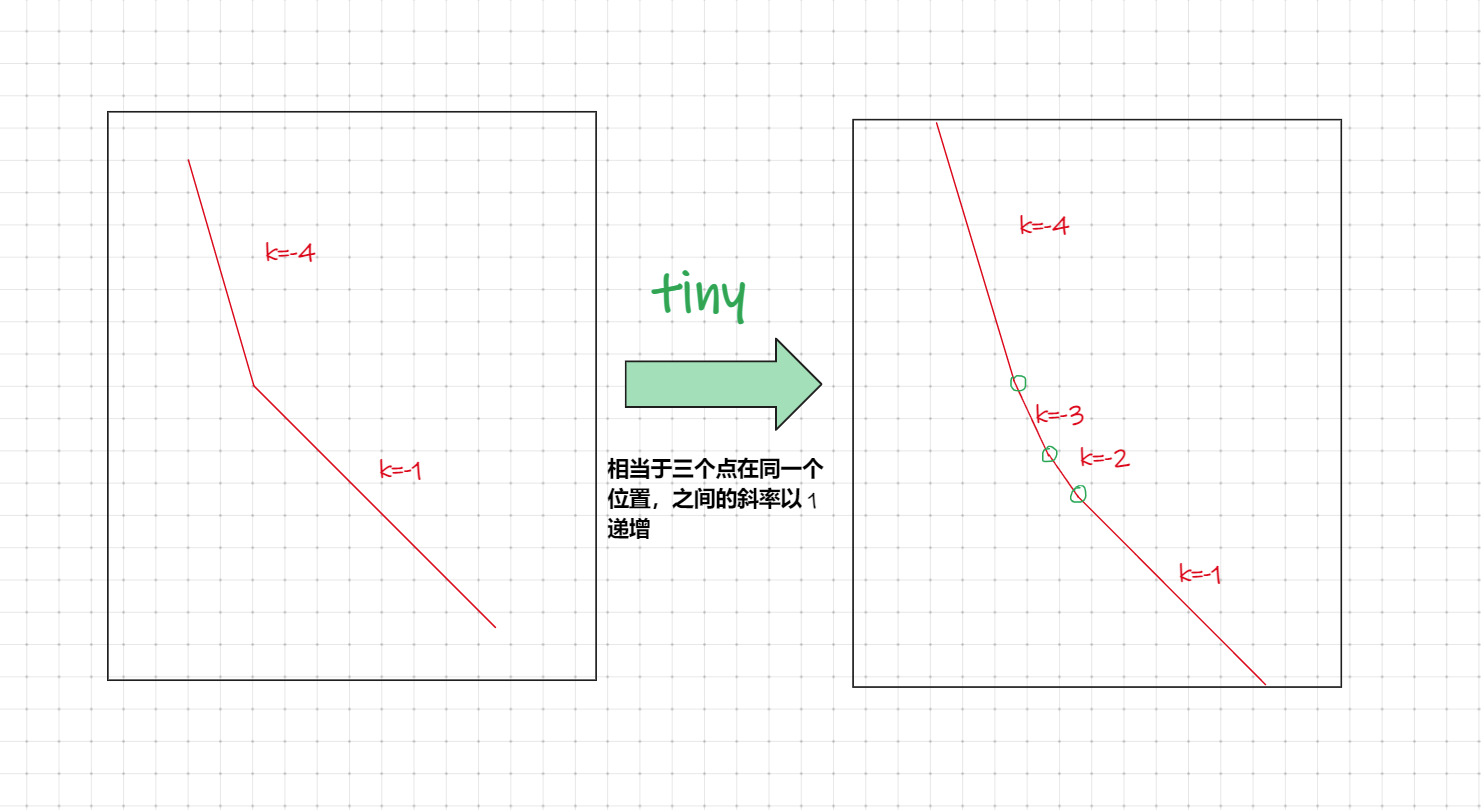
然后加上 \(H_i\)，要分类：

\(A_i\ge P_{i-1}\)

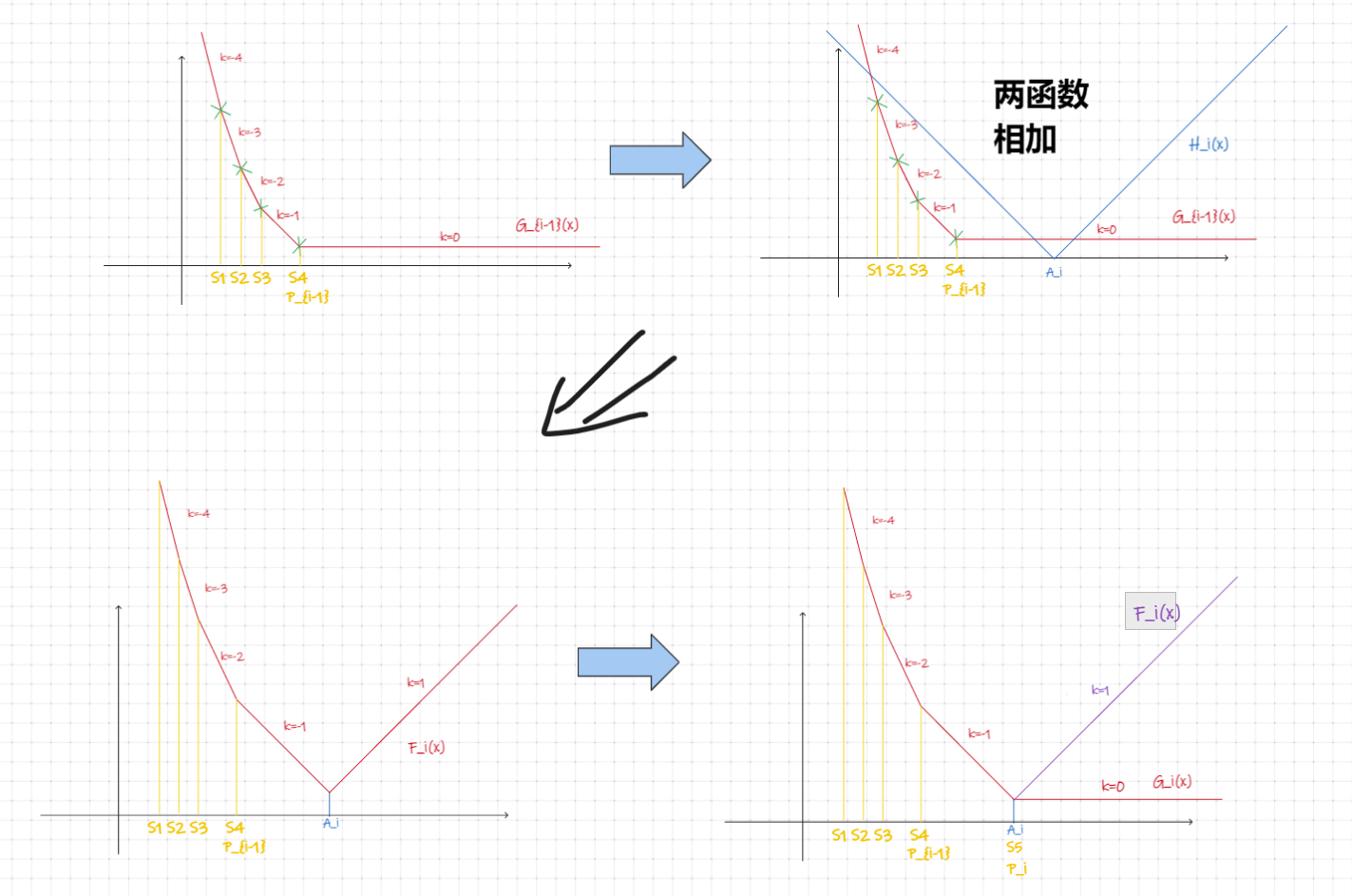
这样答案（为最右边水平部分的 \(y\) 坐标）不变，即

\[\begin{aligned}
F_i(P_i)&=H_i(P_i)+G_{i-1}(P_i)
\\
&=G_{i-1}(P_i)
\\
&=G_{i-1}(P_{i-1})
\\
&=F_{i-1}(P_{i-1})
\end{aligned}
\]

没有贡献。

而且对于 \(\{S\}\)，只用将 \(A_i\) 插入 \(\{S\}\) 末尾即可。

\(A_i<P_{i-1}\)

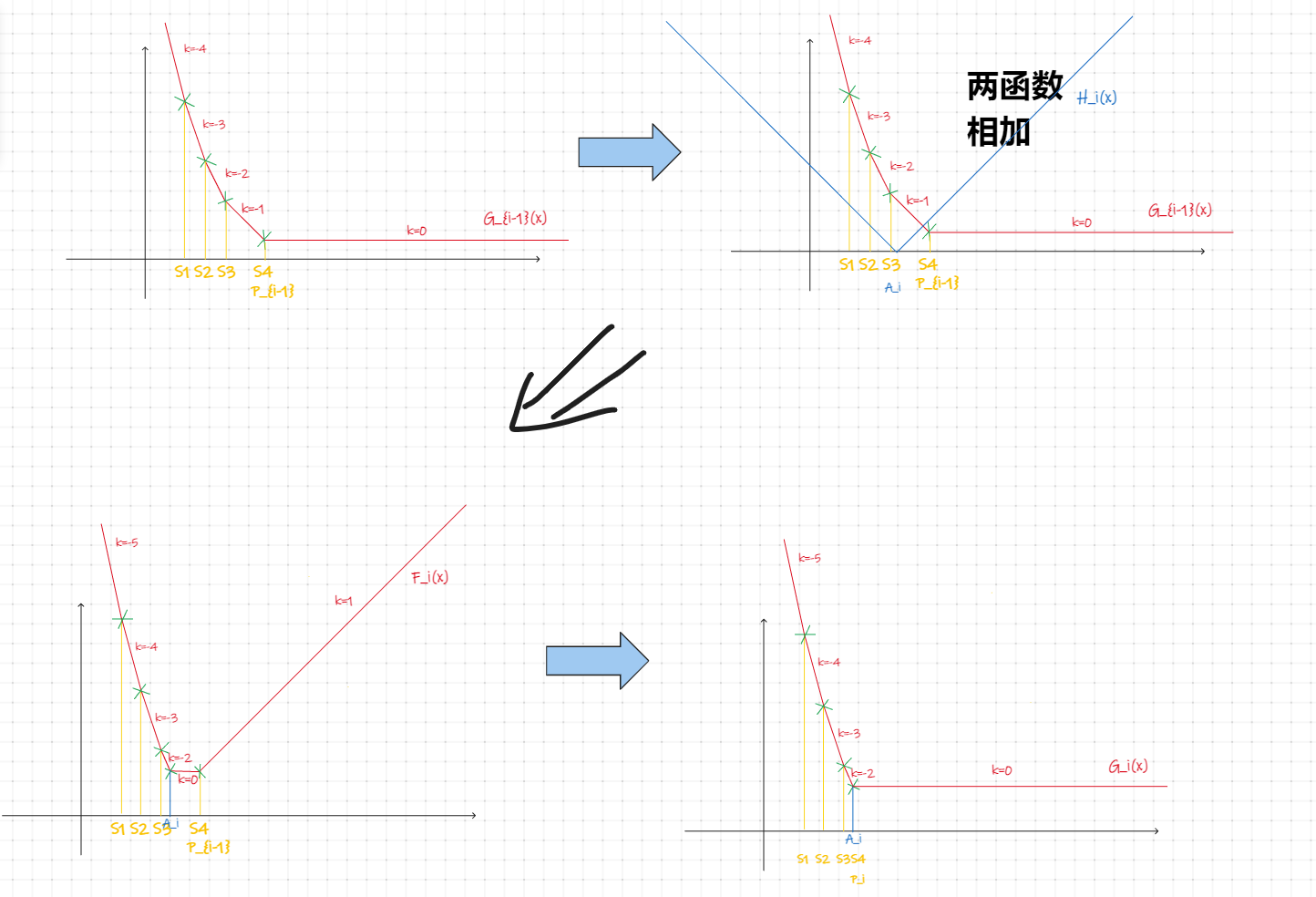
这样答案为

\[\begin{aligned}
F_i(P_i)&=H_i(P_i)+G_{i-1}(P_i)
\\
&=P_i-A_i+F_{i-1}(P_i)
\\
&=P_i-A_i+F_{i-1}(P_{i-1})+P_{i-1}-P_i
\\
&=F_{i-1}(P_{i-1})+P_{i-1}-A_i
\end{aligned}
\]

即增加

\[F_i(P_i)-F_i(P_{i-1})=P_{i-1}-A_i
\]

所以将 \(Ans+\!=P_{i-1}-A_i\)。

此时 \(A_i\) 插入 \(\{S\}\) 要两次，因为他是绝对值函数的转折点，所以两边斜率差值为 \(2\)。

---

相信很多人都蒙了，我们具象一下。

想象有一条左右无限长的铁丝。

初始化：一开始平放在高度 \(0\) 的位置（\(F_0(x)=G_0(x)=0\)）

然后进行 \(n\) 次操作，第 \(i\) 次：

1. 铁丝横坐标为 \(A_i\) 的地方用尖嘴钳固定住。

2. 将尖嘴钳左边的部分向上翘 \(1\) 单位的斜率（这部分铁丝每一点都要弯 \(1\) 斜率）。

3. 尖嘴钳右边的部分同理向上翘 \(1\) 单位的斜率。这样整条铁丝更像「U」形。

这样我们从 \(G_{i-1}\) 得到了 \(F_i\)。

1. 将右边翘起的部分压平。即在右边找到一个点使得这里的铁丝是水平的（导数为 \(0\)）然后从这里往右全部捋成水平的。

这样我们从 \(F_i\) 得到了 \(G_i\)。

1. 松开尖嘴钳。

最后答案为整个铁丝的最低高度值。

相信前文仔细阅读的小可爱们一定懂了这段扭铁丝具体在对凸函数干嘛……

---

所以用堆维护 \(S_1,S_2,\dots,S_c\) 即可。

总时间 \(O(n\log n)\)。

代码？

int n,x,ans=0,b[N];
priority_queue<int> q;
int main(){
	cin>>n;
	For(i,1,n){
		cin>>x;
		q.push(x);
		if(q.top()!=x){
			ans+=q.top()-x;
			q.pop();
			q.push(x);
		}
		b[i]=q.top();
	}
	Rof(i,n-1,1) ckmn(b[i],b[i+1]);
	cout<<ans<<endl;
	For(i,1,n) cout<<b[i]<<" "; cout<<endl;
	return 0;
}

更多？

当然，Slope Trick 不止这种建模和推导。

为了证明这一点，我们再举一个例子。

题面

题目：abc250_g Stonks

大意：

已知接下来 \(n(\le 2\times 10^5)\) 天的股票价格 \(1\le P_1,P_2,\dots,P_n\le 10^9\)。

每天你可以（三选一）：

• 买进一股股票
• 卖出一股股票
• 什么也不做

\(n\) 天之后你拥有的股票应为 \(0\)。

你最初有足够多的钱，求 \(n\) 天结束后能获得的最大利润。

解答

带悔贪心

我们可以快速想出一种贪心策略：买入价格最小的股票，在可以赚钱的当天卖出。

显然我们可以发现，上面的贪心策略是错误的，因为我们买入的股票可以等到可以赚最多的当天在卖出。

我们考虑设计一种反悔策略，使所有的贪心情况都可以得到全局最优解。（即设计反悔自动机的反悔策略）

我们先把当前的价格放入小根堆一次（这次是以上文的贪心策略贪心），判断当前的价格是否比堆顶大，若是比其大，我们就将差值计入全局最优解，再将当前的价格放入小根堆（这次是反悔操作）。相当于我们把当前的股票价格若不是最优解，就没有用，最后可以得到全局最优解。

上面的等式即被称为反悔自动机的反悔策略，因为我们并没有反复更新全局最优解，而是通过差值消去中间项的方法快速得到的全局最优解。

Slope Trick

首先我们考虑最朴素的 \(O(n^2)\) DP 做法：\(f_{i,j}\) 表示前 \(i\) 天过完，现在手上 \(j\) 张股票，所盈利的最大价值。

\[f_{i,j}=\max\{f_{i-1,j+1}+P_i\, ,\, f_{i-1,j}\, ,\, f_{i-1,j-1}-P_i\}
\]

然后我们设函数 \(F_i(x)=f_{i,x}\)（老套路了）。

\[F_i(x)=\max\{F_{i-1}(x+1)+P_i\, ,\, F_{i-1}(x)\, ,\, F_{i-1}(x-1)-P_i\}
\]

也就是说将函数 \(F_{i-1}\)

• 向上 \(P_i\) 单位，向左 \(1\) 单位复制一份，设为 \(F^+_{i-1}\)。
• 向下 \(P_i\) 单位，向右 \(1\) 单位复制一份，设为 \(F^-_{i-1}\)。
• 自己 \(F_{i-1}\) 也保留。

再求三者的上凸包（\(\max\)）即为 \(F_i\)。

这里引用 Atcoder 官方题解的图：

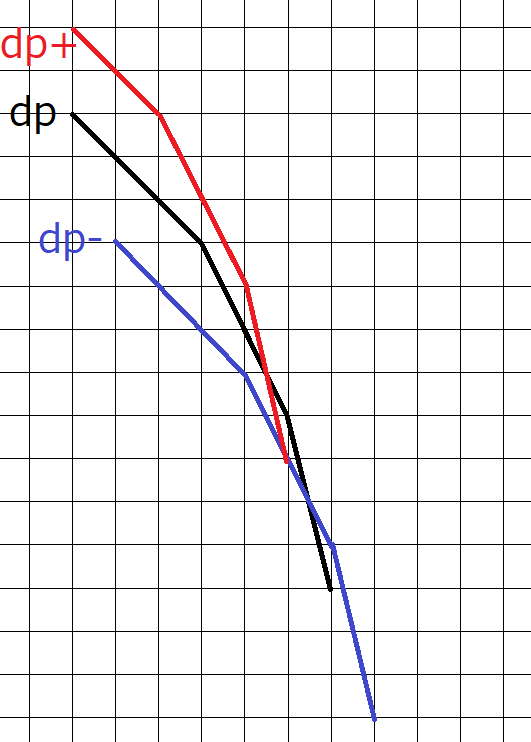
我们发现 \(F_{i-1}\) 只有左边斜率 \(>-P_i\) 且右边斜率 \(<-P_i\) 的点才会相对于 \(F_{i-1}^+,F_{i-1}^-\)「露在外面」。

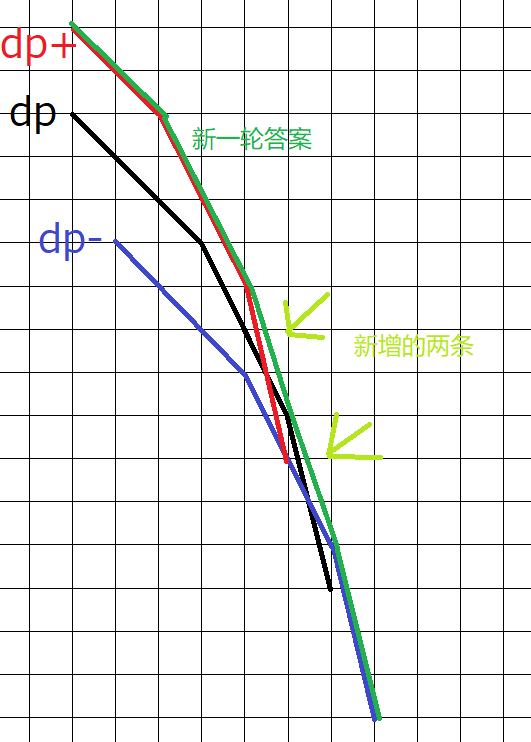
这时会在本来的斜率序列中插入两个斜率为 \(-P_i\) 的线段，同时将本来最靠左的线段去掉。所以用堆维护这个斜率序列，插入两个 \(P_i\)，弹出一次堆顶。

当然，如果 \(P_i\) 小于堆顶，则只要插入 \(P_i\) 即可。

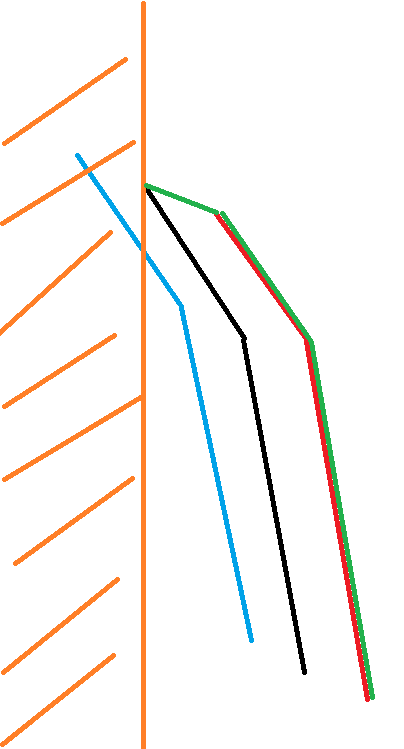
代码

两种解法代码一样神奇吧。

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define For(i,j,k) for(int i=j;i<=k;i++)
#define int long long
#define N 200010

int n,ans=0,x;
priority_queue<int,vector<int>,greater<int> > q;
signed main(){IOS;
	cin>>n;
	For(i,1,n){
		cin>>x;
		if(i!=1 && q.top()<x){
			ans+=x-q.top();
			q.pop();
			q.push(x);
		}
		q.push(x);
	}
	cout<<ans<<endl;
return 0;}