[Java]排序算法>插入排序>【折半插入排序】(O(N*N)/稳定/N较大/无序/顺序存储)

1 折半插入排序

1.1 算法思想

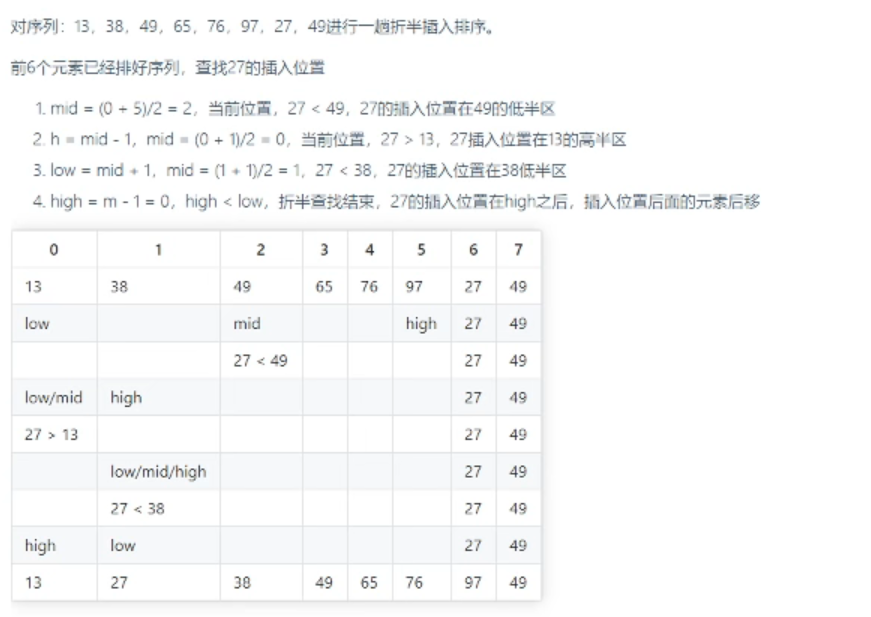
相比于【直接插入排序】：采用“顺序查找法”查找当前记录在已排好序的序列中的插入位置，

折半插入排序利用“折半查找法”快速查出目标插入位置，再针对性滴移动元素，实现插入。

1.2 算法特征

• 属于【插入排序】
  • 直接插入排序
  • 折半插入排序
  • 希尔排序
• 适用于【稳定性】：稳定
• 适用于【规模N】：较大
• 适用于【有序性】：无序
• 适用于【存储结构】：仅顺序存储结构（链式存储难以实现）
• 【时间复杂度】：O(NlogN) (最好) / O(NN) (平均) / O(NN) (最坏)
• 【空间复杂度】：O(1) (最好/平均/最坏)
• 相关口诀：【二希堆快】顺序存，【插冒二选】时N方

1.3 算法实现

import java.util.Arrays;

public class BinInsertSort {
    public static int [] binInsertSort(int []array){//折半插入排序
        int [] resultArray = Arrays.copyOfRange(array, 0, array.length);
        int inertingValue;
        for(int i=1;i<resultArray.length;i++){
            inertingValue = resultArray[i];
            if(resultArray[i-1] > inertingValue){
                int low = 0;
                int high = i-1;
                while(low<=high){
                    int mid = (low+high)/2;
                    if(resultArray[mid]>inertingValue)
                        high = mid-1;
                    else if(resultArray[mid]<inertingValue)
                        low = mid+1;
                }
                //查找结束后，low = high+1 即 应当插入的目标位置
                //后移 下标∈[low, i-1]的元素
                for(int k=i;k>low;k--){//k∈[low+1 , i]
                    resultArray[k] = resultArray[k-1];
                }
                resultArray[low] = inertingValue;
            }
        }
        return resultArray;
    }
}

1.4 测试实现

import java.util.Scanner;

public class Main {
    public static void print(int[] array){
        if(array==null || array.length<1){
            return;
        }
        for(int i=0;i<array.length-1;i++){
            System.out.print(array[i]+" ");
        }
        System.out.println(array[array.length-1]);
    }

    public static void main(String[] args) {
        //1 输入 一组 乱序的数值 数组
        Scanner scanner = new Scanner(System.in);
        String input = scanner.nextLine();
        String [] strValues = input.trim().split(" ");
        int [] array = new int[strValues.length];
        for(int i=0,len=strValues.length;i<len;i++){
            array[i] = Integer.valueOf(strValues[i]).intValue();//假定所有输入均为合规的整型数值
        }
//        print(array);// test - 输出 所输入的数据

        //2 排序
        int [] sortedArray = BinInsertSort.binInsertSort(array);
        //3 输出
        print(sortedArray);
    }
}

1.5 参考文献

• 《数据结构（C语言-第2版-严蔚敏 吴伟民 著）》：Page238