机器学习算法(二): 基于鸢尾花数据集的朴素贝叶斯(Naive Bayes)预测分类
机器学习算法(二): 基于鸢尾花数据集的朴素贝叶斯(Naive Bayes)预测分类
项目链接参考:https://www.heywhale.com/home/column/64141d6b1c8c8b518ba97dcc
1. 实验室介绍
1.1 实验环境
1. python3.7
2. numpy >= '1.16.4'
3. sklearn >= '0.23.1'
1.2 朴素贝叶斯的介绍
朴素贝叶斯算法(Naive Bayes, NB) 是应用最为广泛的分类算法之一。它是基于贝叶斯定义和特征条件独立假设的分类器方法。由于朴素贝叶斯法基于贝叶斯公式计算得到,有着坚实的数学基础,以及稳定的分类效率。NB模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。当年的垃圾邮件分类都是基于朴素贝叶斯分类器识别的。
什么是条件概率,我们从一个摸球的例子来理解。我们有两个桶:灰色桶和绿色桶,一共有7个小球,4个蓝色3个紫色,分布如下图:
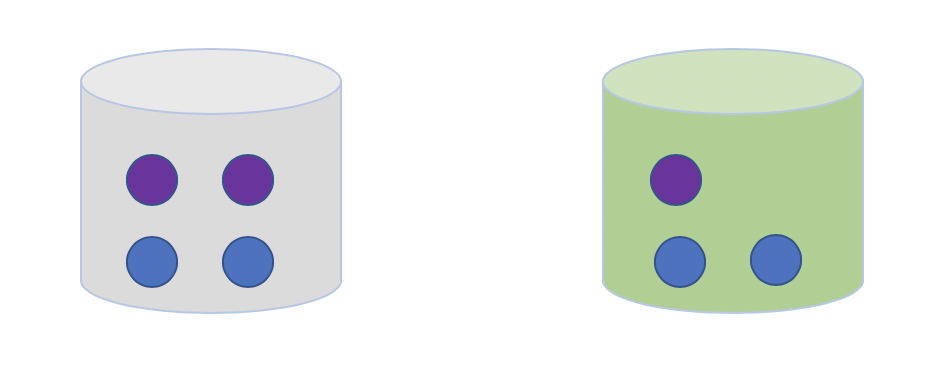
从这7个球中,随机选择1个球是紫色的概率p是多少?选择过程如下:
- 先选择桶
- 再从选择的桶中选择一个球
$$
p(球=紫色) \
=p(选择灰桶) \cdot p(从灰桶中选择紫色) + p(选择绿桶) \cdot p(从灰桶中选择紫色) \
=\frac{1}{2} \cdot \frac{2}{4} + \frac{1}{2} \cdot \frac{1}{2}
$$
上述我们选择小球的过程就是条件概率的过程,在选择桶的颜色的情况下是紫色的概率,另一种计算条件概率的方法是贝叶斯准则。
贝叶斯公式是英国数学家提出的一个数据公式:
$$
p(A|B)=\frac{p(A,B)}{p(B)}=\frac{p(B|A) \cdot p(A)}{\sum_{a \in ℱ_A}p(B|a) \cdot p(a)}
$$
p(A,B):表示事件A和事件B同时发生的概率。
p(B):表示事件B发生的概率,叫做先验概率;p(A):表示事件A发生的概率。
p(A|B):表示当事件B发生的条件下,事件A发生的概率叫做后验概率。
p(B|A):表示当事件A发生的条件下,事件B发生的概率。
我们用一句话理解贝叶斯:世间很多事都存在某种联系,假设事件A和事件B。人们常常使用已经发生的某个事件去推断我们想要知道的之间的概率。
例如,医生在确诊的时候,会根据病人的舌苔、心跳等来判断病人得了什么病。对病人来说,只会关注得了什么病,医生会通道已经发生的事件来
确诊具体的情况。这里就用到了贝叶斯思想,A是已经发生的病人症状,在A发生的条件下是B_i的概率。
1.3 朴素贝叶斯的应用
朴素贝叶斯算法假设所有特征的出现相互独立互不影响,每一特征同等重要,又因为其简单,而且具有很好的可解释性一般。相对于其他精心设计的更复杂的分类算法,朴素贝叶斯分类算法是学习效率和分类效果较好的分类器之一。朴素贝叶斯算法一般应用在文本分类,垃圾邮件的分类,信用评估,钓鱼网站检测等。
2. 实验室手册
2.1 学习目标
- 掌握贝叶斯公式
- 结合两个实例了解贝朴素叶斯的参数估计
- 掌握贝叶斯估计
2.2 代码流程
Part 1. 莺尾花数据集--贝叶斯分类
- Step1: 库函数导入
- Step2: 数据导入&分析
- Step3: 模型训练
- Step4: 模型预测
- Step5: 原理简析
Part 2. 模拟离散数据集--贝叶斯分类
- Step1: 库函数导入
- Step2: 数据导入&分析
- Step3: 模型训练&可视化
- Step4: 原理简析
2.3 算法实战
莺尾花数据集--贝叶斯分类
Step1: 库函数导入
import warnings
warnings.filterwarnings('ignore')
import numpy as np
# 加载莺尾花数据集
from sklearn import datasets
# 导入高斯朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
Step2: 数据导入&分析
X, y = datasets.load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
我们需要计算两个概率分别是:条件概率:$P(X{(i)}=x|Y=c_k)$和类目$c_k$的先验概率:$P(Y=c_k)$。
通过分析发现训练数据是数值类型的数据,这里假设每个特征服从高斯分布,因此我们选择高斯朴素贝叶斯来进行分类计算。
Step3: 模型训练
# 使用高斯朴素贝叶斯进行计算
clf = GaussianNB(var_smoothing=1e-8)
clf.fit(X_train, y_train)
Step4: 模型预测
# 评估
y_pred = clf.predict(X_test)
acc = np.sum(y_test == y_pred) / X_test.shape[0]
print("Test Acc : %.3f" % acc)
# 预测
y_proba = clf.predict_proba(X_test[:1])
print(clf.predict(X_test[:1]))
print("预计的概率值:", y_proba)
Test Acc : 0.967 [2] 预计的概率值: [[1.63542393e-232 2.18880483e-006
9.99997811e-001]]
Step5: 原理简析
高斯朴素贝叶斯假设每个特征都服从高斯分布,我们把一个随机变量X服从数学期望为μ,方差为σ2的数据分布称为高斯分布。对于每个特征我们一般使用平均值来估计μ和使用所有特征的方差估计σ2。
$$
P(X{(i)}=x|Y=c_k) = \frac{1}{\sqrt{2\pi\sigma^2_y}} \exp\left(-\frac{(x^{(i)} - \mu_{c_k})2}{2\sigma2_{c_k}}\right)
$$
从上述例子中的预测结果中,我们可以看到类别2对应的后验概率值最大,所以我们认为类目2是最优的结果。
模拟离散数据集--贝叶斯分类
Step1: 库函数导入
+ Step2: 数据导入&分析
+ Step3: 模型训练&可视化
+ Step4: 原理简析
import random
import numpy as np
# 使用基于类目特征的朴素贝叶斯
from sklearn.naive_bayes import CategoricalNB
from sklearn.model_selection import train_test_split
Step2: 数据导入&分析
# 模拟数据
rng = np.random.RandomState(1)
# 随机生成600个100维的数据,每一维的特征都是[0, 4]之前的整数
X = rng.randint(5, size=(600, 100))
y = np.array([1, 2, 3, 4, 5, 6] * 100)
data = np.c_[X, y]
# X和y进行整体打散
random.shuffle(data)
X = data[:,:-1]
y = data[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
所有的数据特征都是离散特征,我们引入基于离散特征的朴素贝叶斯分类器。
Step3: 模型训练&预测
clf = CategoricalNB(alpha=1)
clf.fit(X_train, y_train)
acc = clf.score(X_test, y_test)
print("Test Acc : %.3f" % acc)
Test Acc : 0.683
# 随机数据测试,分析预测结果,贝叶斯会选择概率最大的预测结果
# 比如这里的预测结果是6,6对应的概率最大,由于我们是随机数据
# 读者运行的时候,可能会出现不一样的结果。
x = rng.randint(5, size=(1, 100))
print(clf.predict_proba(x))
print(clf.predict(x))
[[3.48859652e-04 4.34747491e-04 2.23077189e-03 9.90226387e-01
5.98248900e-03 7.76745425e-04]]
2.4 原理简析
2.4.1 结果分析
可以看到测试的数据的结果,贝叶斯会选择概率最大的预测结果,比如这里的预测结果是6,6对应的概率最大,由于我们是随机数据,读者运行的时候,可能会出现不一样的结果。
这里的测试数据的准确率没有任何意义,因为数据是随机生成的,不一定具有贝叶斯先验性,这里只是作为一个列子引导大家如何使用。
alpha=1这个参数表示什么?
我们知道贝叶斯法一定要计算两个概率:条件概率:$P(X{(i)}=x|Y=c_k)$和类目$c_k$的先验概率:$P(Y=c_k)$。
对于离散特征:
$$
P(X{(j)}=x|Y=c_k)=\frac{\sum_{i=1}{N}I(x_ij=a_{jl},y_i=c_k)+\alpha}{\sum_{i=1}^{N}I(y_i=c_k)+S_j\alpha}
$$
我们可以看出就是对每一个变量的多加了一个频数alpha。当alphaλ=0时,就是极大似然估计。通常取值alpha=1,这就是拉普拉斯平滑(Laplace smoothing),这有叫做贝叶斯估计,主要是因为如果使用极大似然估计,如果某个特征值在训练数据中没有出现,这时候会出现概率为0的情况,导致整个估计都为0,因为引入贝叶斯估计。
其中:
$S_j$:表示第j个特征的个数。
$x_i^j$:表示第i个样本的第j维元素。
$y_i$:第i个样本的label。
2.4.2 朴素贝叶斯算法
朴素贝叶斯法 = 贝叶斯定理 + 特征条件独立。
输入$X \in R^n$空间是n维向量集合,输出空间$y={c_1,c_2,...,c_K}$. 所有的X和y都是对应空间上的随机变量. $P(X,Y)$是X和Y的联合概率分别. 训练数据集(由$P(X,Y)$独立同分布产生):
$$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$$
计算测试数据x的列表,我们需要依次计算$P(Y=c_k|X=x)$,取概率最大的值,就是x对应的分类。
$P(Y=c_k|X=x)$我们一般这样解释,当给定$(X=x)$的条件下,$Y=c_k$的概率,这就是条件概率. 这就简单了,我们只需要每个的x,计算其对应的$c_k,k \in [1,2,...,K]$的概率,选择最大的概率作为这个x的类别进行了.
通过贝叶斯公式进行变形,得到预测的概率计算公式:
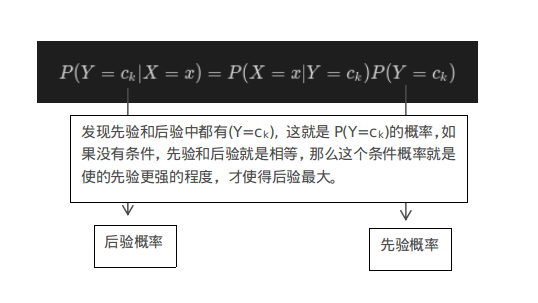
$$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_{k}P(X=x|Y=c_k)P(Y=c_k)}$$
我们只需要计算以下两个概率即可,又由于朴素贝叶斯假设条件独立,我们可以单独计算每个特征的条件概率:$P(X{(i)}=x|Y=c_k)$和类目$c_k$的先验概率:$P(Y=c_k)$。为了更好的理解这个公式,看下图解释:
其中:
$$
P(Y=c_k)=\frac{\sum_{i=1}^{N}I(y_i=c_k)}{N}, k=1,2,...,K
$$
当涉及到多个条件时,朴素贝叶斯有一个提前的假设,我们称之为 条件独立性假设(或者 简单假设:Naive):公式如下
$$
P(A,B|Y) = P(A|Y) \cdot P(B|Y)
$$
这个公式是朴素贝叶斯的基础假设,即各个条件概率是相互独立的,A不影响B,B不影响A。
而对这里来说,假设$X = [x_1,x_2,...,x_n]$
$$
P(X=x|Y=c_k) \
=P(X{(1)}=x,X{(2)}=x,...,X{(n)}=x|Y=c_k) \
=\prod_{i=1}^{n} P(x_i | y)
$$
由此原式可以等价为:
$$P(Y=c_k|X=x)=\frac{\prod_{i=1}^{n} P(x_i | Y=c_k)P(Y=c_k)}{\sum_{k}\prod_{i=1}^{n} P(x_i | Y=c_k)P(Y=c_k)}$$
我们为了选择后验概率最大的结果,进行概率的比较,由于分母一致,这里直接去掉分母,得到最后的计算公式。
$$
y=arg max_{c_k}P(Y=c_k)\prod_{j}P(X{(j)}=x|Y=c_k)
$$
我们来看一个实例,更好的理解贝叶斯的计算过程,根据天气和是否是周末预测一个人是否会出门。
| index | $X_1:$天气的好坏 | $X_2:$是否周末 | $Y:$是否出门 |
|---|---|---|---|
| 1 | 好 | 是 | 出门 |
| 2 | 好 | 否 | 出门 |
| 3 | 好 | 是 | 不出门 |
| 4 | 好 | 否 | 出门 |
| 5 | 不好 | 是 | 出门 |
| 6 | 不好 | 否 | 不出门 |
根据上述数据,为了更好的理解计算过程,我们给出几个计算公式:
a. 当出门的条件下,X_1是天气不好的概率:
$$
p(X_1=不好|Y=出门)
=\frac{p(X_1=不好,Y=出门)}{p(Y=出门)}=\frac{1}{4}
$$
b. 出门的概率
$$
p(Y=出门)=\frac{4}{6}
$$
c. X_1天气不好的概率、
$$
p(X_1=不好)=\frac{2}{6}
$$
d. 在X_1天气不好的情况下,出门的概率:
$$
p(Y=出门|X_1=不好)=\frac{p(X_1=不好|Y=出门) \cdot p(Y=出门)}{p(X=不好)} \
=\frac{\frac{1}{4} \cdot \frac{4}{6}}{\frac{2}{6}}=\frac{1}{2}
$$
f. 在X_1天气不好的情况下,不出门的概率:
$$
p(Y=出门|X_1=不好)=1-p(Y=不出门|X_1=不好)=1-\frac{1}{2}=\frac{1}{2}
$$
2.4.3 朴素贝叶斯的优缺点
优点:
朴素贝叶斯算法主要基于经典的贝叶斯公式进行推倒,具有很好的数学原理。而且在数据量很小的时候表现良好,数据量很大的时候也可以进行增量计算。由于朴素贝叶斯使用先验概率估计后验概率具有很好的模型的可解释性。
缺点:
朴素贝叶斯模型与其他分类方法相比具有最小的理论误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进,例如为了计算量不至于太大,我们假定每个属性只依赖另外的一个。解决特征之间的相关性,我们还可以使用数据降维(PCA)的方法,去除特征相关性,再进行朴素贝叶斯计算。
机器学习算法(二): 基于鸢尾花数据集的朴素贝叶斯(Naive Bayes)预测分类的更多相关文章
- 机器学习算法实践:朴素贝叶斯 (Naive Bayes)(转载)
前言 上一篇<机器学习算法实践:决策树 (Decision Tree)>总结了决策树的实现,本文中我将一步步实现一个朴素贝叶斯分类器,并采用SMS垃圾短信语料库中的数据进行模型训练,对垃圾 ...
- 朴素贝叶斯 Naive Bayes
2017-12-15 19:08:50 朴素贝叶斯分类器是一种典型的监督学习的算法,其英文是Naive Bayes.所谓Naive,就是天真的意思,当然这里翻译为朴素显得更学术化. 其核心思想就是利用 ...
- 【机器学习速成宝典】模型篇05朴素贝叶斯【Naive Bayes】(Python版)
目录 先验概率与后验概率 条件概率公式.全概率公式.贝叶斯公式 什么是朴素贝叶斯(Naive Bayes) 拉普拉斯平滑(Laplace Smoothing) 应用:遇到连续变量怎么办?(多项式分布, ...
- 什么是机器学习的分类算法?【K-近邻算法(KNN)、交叉验证、朴素贝叶斯算法、决策树、随机森林】
1.K-近邻算法(KNN) 1.1 定义 (KNN,K-NearestNeighbor) 如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类 ...
- Stanford大学机器学习公开课(六):朴素贝叶斯多项式模型、神经网络、SVM初步
(一)朴素贝叶斯多项式事件模型 在上篇笔记中,那个最基本的NB模型被称为多元伯努利事件模型(Multivariate Bernoulli Event Model,以下简称 NB-MBEM).该模型有多 ...
- 手写朴素贝叶斯(naive_bayes)分类算法
朴素贝叶斯假设各属性间相互独立,直接从已有样本中计算各种概率,以贝叶斯方程推导出预测样本的分类. 为了处理预测时样本的(类别,属性值)对未在训练样本出现,从而导致概率为0的情况,使用拉普拉斯修正(假设 ...
- 【Spark机器学习速成宝典】模型篇04朴素贝叶斯【Naive Bayes】(Python版)
目录 朴素贝叶斯原理 朴素贝叶斯代码(Spark Python) 朴素贝叶斯原理 详见博文:http://www.cnblogs.com/itmorn/p/7905975.html 返回目录 朴素贝叶 ...
- 机器学习Sklearn系列:(四)朴素贝叶斯
3--朴素贝叶斯 原理 朴素贝叶斯本质上就是通过贝叶斯公式来对得到类别概率,但区别于通常的贝叶斯公式,朴素贝叶斯有一个默认条件,就是特征之间条件独立. 条件概率公式: \[P(B|A) = \frac ...
- tf-idf、朴素贝叶斯的短文本分类简述
朴素贝叶斯分类器(Naïve Bayes classifier)是一种相当简单常见但是又相当有效的分类算法,在监督学习领域有着很重要的应用.朴素贝叶斯是建立在“全概率公式”的基础下的,由已知的尽可能多 ...
- python实现随机森林、逻辑回归和朴素贝叶斯的新闻文本分类
实现本文的文本数据可以在THUCTC下载也可以自己手动爬虫生成, 本文主要参考:https://blog.csdn.net/hao5335156/article/details/82716923 nb ...
随机推荐
- C++ push_back()函数应用
最近在学习Opencv,用C++写程序,做了一个虚拟画笔的项目,即通过摄像头采集视频图像信息,识别视频中的画笔,并画笔在空中的划痕显示在视频图像上.在进行到划痕显示的,由于视频是实时采集的,检测到的画 ...
- mysql零基础-2
更新中的数据完整性错误 UPDATE employees SET department_id = 55 WHERE department_id = 110; 删除数据 删除一条记录 DELETE FR ...
- python音乐分类--knn
1 #利用knn算法分类音乐,将音乐进行情绪分类 2 #将音乐分为兴奋的(excited), 愤怒的(angry),悲伤的(sorrowful),轻松的(relaxed) 3 4 #可分离因素 5 # ...
- 解决IOS上传竖向照片会旋转90度的问题
// 解决IOS上传竖向照片会旋转90度的问题 rotate() { const that = this; that.imgOrientation = 1; let Orientation = nul ...
- ffmpeg安装教程
1 下载所需要的软件 mkdir /usr/local/soft cd /usr/local/soft wget https://www.ffmpeg.org/releases/ffmpeg-snap ...
- 浏览器上验证xpath元素是否正确
一.验证元素定位 Chrome的console可以用来验证XPath和CSS. 1.验证XPath 1.输入:$x("your_xpath_selector")2.输入完毕后,点击 ...
- MongoDB 相关的一些操作
一. 在 MongoDB Compass中输入条件查询数据 {"src":"小车"} // = 该值 {"src":{$ ...
- linux 串口查看信息
查看串口是否可用,可以对串口发送数据比如对com1口,echo helloworld >/dev/ttyS0 [root@H3LINUX90 ~]# echo helloworld >/d ...
- B树、B+树详解
B树.B+树详解 B树 前言 首先,为什么要总结B树.B+树的知识呢?最近在学习数据库索引调优相关知识,数据库系统普遍采用B-/+Tree作为索引结构(例如mysql的InnoDB引擎使用的B+树 ...
- PHP中获取时间的下一周下个月的方法
PHP中获取时间的下一周,下个月等通常用于定制服务的时候使用,比如包月会员,包年等等 //通常用于定制服务的时候使用,比如包月会员,包年等等 //获取当前时间过一个月的时间,以DATETIME格式显示 ...
