[0x11] 131.直方图中最大的矩形【单调栈】

题意

link（more：SPOJ1805）

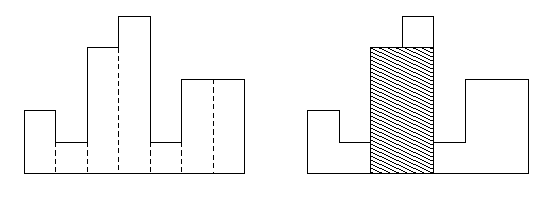
如图，在水平线上有 \(n(n\leqslant10^5)\) 个宽度为 1 ，高度为 \(h(0\leqslant h\leqslant10^9)\) 的矩形，求包含于其中的最大子矩形面积。

例： \(h=\{2,1,4,5,1,3,3\};S_{max}=S_{阴影}\)

思路

朴素

首先简单模拟过程，可知当前高度受 \(h_i\) 的限制，以此向左右尽量扩边界 \(l_i,r_i\) ，得到当高度为 \(h_i\) 时的最大子矩形，在图中表现为：

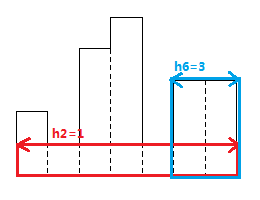
不难看出，当 \(l_i,r_i\) 遇到第一个高度比 \(h_i\) 低的矩形时，就达到了最大边界。

∴易想到枚举所有矩形，每次向左右枚举得到 \(l_i,r_i\) 算出当前面积。

但该算法最坏复杂度显然达到 \(O(n^2)\) ，妥妥的超时。

优化

那么就必须得用 \(O(1)\) 的时间得到 \(l_i,r_i\) 才能降到 \(O(n)\) 通过此题。

由于求 \(l_i,r_i\) 是对称的，接下来考虑一边 \(l_i\) ：

我们从左往右观察每个子矩形 \(l_i\) 的推导过程，若 \(h_j<h_i\) ，那么前 \(k(k\in[1,j-1])\) 个对于 求当前子矩形边界 就没有任何意义了。

继续推广，我们同时要考虑到后 \(k(k\in[i+1,n])\) 个矩形中可能有 \(h_k<h_i\) 的情况。

也就是说，如果全局性考虑的话，在前 \(k(k\in[1,j-1])\) 个其中 \(h_k<h_j\) 的矩形 仍是有潜力成为边界的 ，就需要保留。

---

基于上述所说，我们可以这样考虑：

显然要把 \(h_i\) 放入一个数据结构里处理，在尾端作插入和删除操作。（就是栈啦）

现在考虑一个中间状态，将要进来 \(h_i\) ，前面已经放入 \(k\) 个矩形了。

我们要找第一个 \(h_j<h_i(j\in[1,k])\) ，那么在栈中就可以把\(h_j\geqslant h_i\) 的删掉，模拟一下样例：

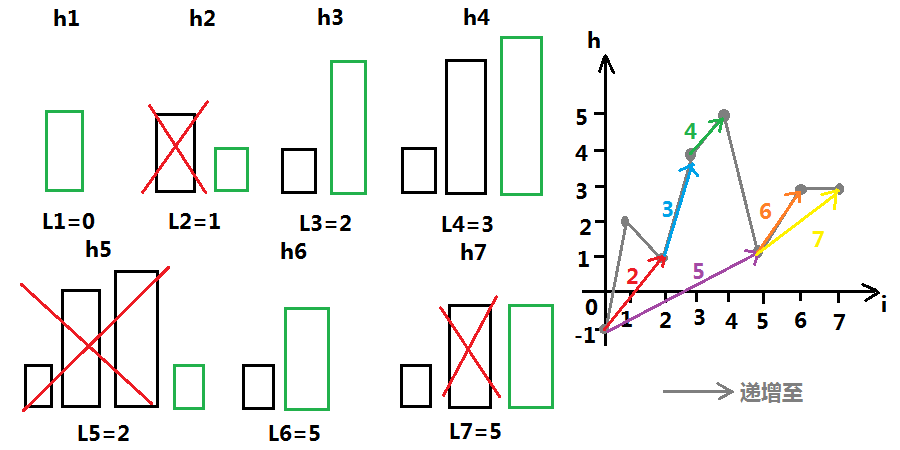
可知，在栈中，矩阵高度保持 单调性 ，且是单调递增，这就是 单调栈 。

有了单调性，就可以 \(O(1)\) 的时间得到 \(l_i\) .

code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,h[N],l[N],r[N],s[N],t;
int main()
{
    while(cin>>n,n)
    {
        for(int i=1;i<=n;i++) cin>>h[i];
        h[0]=h[n+1]=-1;//边界
        t=0;
        s[t]=0;//先存进边界编号
        for(int i=1;i<=n;i++)
        {
            while(h[s[t]]>=h[i]) t--;
            l[i]=s[t];
            s[++t]=i;
        }
        t=0;
        s[t]=n+1;
        for(int i=n;i>=1;i--)
        {
            while(h[s[t]]>=h[i]) t--;
            r[i]=s[t];
            s[++t]=i;
        }
        ll ans=0;
        for(int i=1;i<=n;i++)
            ans=max(ans,(ll)h[i]*(r[i]-l[i]-1));
        cout<<ans<<endl;
    }
    return 0;
}

总结

单调栈思想：及时排除不可能的选项，保持策略集合的高度有效性和秩序性。