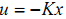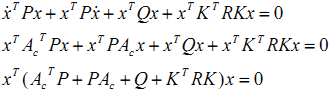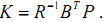LQR (线性二次型调节器)的直观推导及简单应用
转自:https://blog.csdn.net/heyijia0327/article/details/39270597
本文主要介绍LQR的直观推导,说明LQR目标函数J选择的直观含义以及简单介绍矩阵Q,R的选取,最后总结LQR控制器的设计步奏,并将其应用在一个简单的倒立摆例子上。
假设有一个线性系统能用状态向量的形式表示成:
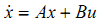
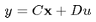 ( 1 )
( 1 )
其中 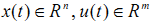
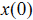
在介绍LQR前,先简单回顾一下现代控制理论中最基本的控制器--全状态反馈控制。
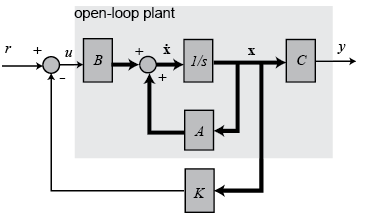
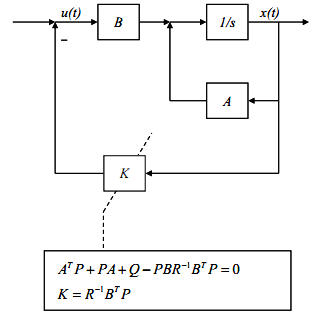
全状态反馈控制系统图形如下:
我们要设计一个状态反馈控制器
使得闭环系统能够满足我们期望的性能。我们把这种控制代入之前的系统状态方程得到
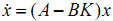 ( 2 )
( 2 )
对于(1)式的开环系统,由现代控制理论我们知道开环传递函数的极点就是系统矩阵A的特征值。
(传递函数的分母是|s| -A|,|·|表示行列式)
现在变成了(2)的闭环形式,状态变换矩阵A变成了(A-BK)。因此通过配置反馈矩阵K,可以使得闭环系统的极点达到我们期望的状态。注意,这种控制器的设计与输出矩阵C,D没有关系。
那么,什么样的极点会使得系统性能很棒呢?并且,当系统变量很多的时候,即使设计好了极点,矩阵K也不好计算。
于是,LQR为我们设计最优控制器提供了一种思路。
在设计LQR控制器前,我们得设计一个能量函数,最优的控制轨迹应该使得该能量函数最小。一般选取如下形式的能量函数。
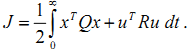
其中Q是你自己设计的半正定矩阵,R为正定矩阵。
可是,为什么能量函数(或称系统的目标函数)得设计成这个样子呢?
首先假设状态向量x(t)是1维的,那么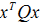
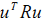
再来看看矩阵Q,R的选取,一般来说,Q值选得大意味着,要使得J小,那x(t)需要更小,也就是意味着闭环系统的矩阵(A-BK)的特征值处于S平面左边更远的地方,这样状态x(t)就以更快的速度衰减到0。另一方面,大的R表示更加关注输入变量u(t),u(t)的减小,意味着状态衰减将变慢。同时,Q为半正定矩阵意味着他的特征值非负,R为正定矩阵意味着它的特征值为正数。如果你选择Q,R都是对角矩阵的话,那么Q的对角元素为正数,允许出现几个0.R的对角元素只能是正数。
注意LQR调节器是将状态调节到0,这与轨迹跟踪不同,轨迹跟踪是使得系统误差为0。
轨迹跟踪实现方案线性二次型控制器(LQR)——轨迹跟踪器
知道了背景后,那如何设计反馈矩阵K使得能量函数J最小呢?
很多地方都是从最大值原理,Hamilton函数推导出来。这里用另外一种更容易接受的方式推导。
将u = -Kx 代入之前的能量函数得到:
 ( 3 )
( 3 )
为了找到K,我们先不防假设存在一个常量矩阵P使得:
 (4)
(4)
代入(3)式得:
 (5)
(5)
注意,我们已经假设闭环系统是稳定的,也就是t趋于无穷时,x(t)趋于0.
现在把(4)式左边的微分展开,并把状态变量x的微分用(2)式替代得到:
这个式子要始终成立的话,括号里的项必须恒等于0.

这是一个关于K的二次型等式,当然这个二次型是我们不愿看到的,因为计算复杂。现在只要这个等式成立,我们何必不选择K使得两个二次项正好约掉了呢?这样既符合了要求,又简化了计算。
取 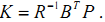 代入上式得:
代入上式得:
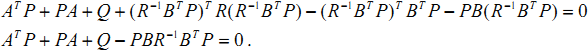
K的二次项没有了,可K的取值和P有关,而P是我们假设的一个量,P只要使得的(6)式成立就行了。而(6)式在现代控制理论中极其重要,它就是有名的Riccati 方程。
现在回过头总结下LQR控制器是怎么计算反馈矩阵K的:
1.选择参数矩阵Q,R
2.求解Riccati 方程得到矩阵P
3.计算
再看看LQR的结构图:
关于它的应用呢,比较典型的就是倒立摆控制器的设计。
倒立摆的状态变量为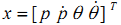
- A = [0 1 0 0
- 0 0 -1 0
- 0 0 0 1
- 0 0 9 0];
- B = [0;0.1;0;-0.1];
- C = [0 0 1 0]; %观测角度
- D = 0;
- Q = [1 0 0 0
- 0 1 0 0
- 0 0 10 0
- 0 0 0 10
- ];
- R = 0.1;
- %由上面这个系统,可以计算出K
- K = lqr(A,B,Q,R);
- Ac = A - B*K;
- %对系统进行模拟
- x0 = [0.1;0;0.1;0]; %初始状态
- t = 0:0.05:20;
- u = zeros(size(t));
- [y,x]=lsim(Ac,B,C,D,u,t,x0);
- plot(t,y);
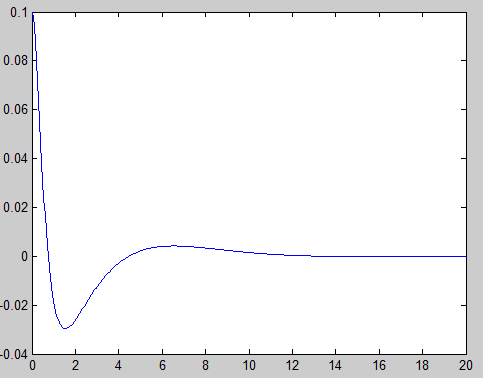
最后看到角度回到0,即平衡位置,控制器起到了作用,你可以选择不同的Q,R进行对比。
文章为总结性文章,有纰漏,请指出,谢谢。
reference:
1.F.L. Lewis .<< Linear Quadratic Regulator (LQR) State Feedback Design >>
2.http://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=ControlStateSpace
3.http://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=ControlStateSpace
LQR (线性二次型调节器)的直观推导及简单应用的更多相关文章
- GRU(Gated Recurrent Unit) 更新过程推导及简单代码实现
GRU(Gated Recurrent Unit) 更新过程推导及简单代码实现 RNN GRU matlab codes RNN网络考虑到了具有时间数列的样本数据,但是RNN仍存在着一些问题,比如随着 ...
- 线性二次型调节器LQR/LQC算法解析及求解器代码(matlab)
参考链接:http://120.52.51.14/stanford.edu/class/ee363/lectures/dlqr.pdf 本文参考讲义中的第20页PPT,根据Hamilton-Jacob ...
- BP神经网络的直观推导与Java实现
人工神经网络模拟人体对于外界刺激的反应.某种刺激经过人体多层神经细胞传递后,可以触发人脑中特定的区域做出反应.人体神经网络的作用就是把某种刺激与大脑中的特定区域关联起来了,这样我们对于不同的刺激就可以 ...
- Android -- 贝塞尔曲线公式的推导和简单使用
1,最近看了几个不错的自定义view,发现里面都会涉及到贝塞尔曲线知识,深刻的了解到贝塞尔曲线是进阶自定义view的一座大山,so,今天先和大家来了解了解. 2,贝塞尔曲线作用十分广泛,简单举几个的栗 ...
- Python3基础 生成器推导式 简单示例
Python : 3.7.0 OS : Ubuntu 18.04.1 LTS IDE : PyCharm 2018.2.4 Conda ...
- Python_迭代器、生成器、列表推导式,生成器表达式
1.迭代器 (1)可迭代对象 s1 = ' for i in s1: print(i) 可迭代对象 示例结果: D:\Python36\python.exe "E:/Python/课堂视频/ ...
- 神经网络前向后向传播(理论推导+代码) 单层神经网络相当于logistic regression
建立神经网络的主要步骤是: 1. 定义模型结构(例如输入特征的数量) 2. 初始化模型的参数 3. 循环: # 3.1 计算当前损失(正向传播) # 3.2 计算当前梯度(反向传播) # 3.3 更新 ...
- javaweb servlet jsp简单笔记
第二章: 1: web 俗称 : 万维网 www 2: web开发 的三大核心: HTML(网页) ,URL(定位),HTTP:(协议) 页面的分类: 静态页面: html+css 动态页面:jsp ...
- 【OI】关于快速幂的简单理解
都知道算某个数的幂需要线性的复杂度,为了优化复杂度,就出现了所谓的快速幂. 快速幂的代码很短,但是要原理需要一点心思. 首先,我们知道, a^b = a^c * a^d (c+d=b) 那么,不就可以 ...
随机推荐
- input框限制输入金额
HTML: <input type="tel" class="capital mui-input-clear" value="0.00" ...
- IDEA 快捷键和字体设置
IDEA的使用 一.IDEA 目录 IDEA的使用 一.IDEA 设置字体 文本字体设置 窗口字体设置 二.IDEA建立项目 三.IDEA快捷键 设置字体 点击File->Settings 文本 ...
- WPF子窗体
效果: 1. 点击WPF主窗体上的一个按钮,弹出子窗体, 2. 窗体最小化后,在菜单栏中点击子窗体,会连带显示它所从属的主窗体. 1. 在WPF项目中,已有主窗体MainWindow,再新建子窗体Ch ...
- ABP Framework 5.2 RC 发布及新增功能介绍
ABP Framework 5.2 RC 新增功能 目录 ABP Framework 5.2 RC 新增功能 单层解决方案模板 EF Core 数据库迁移 UI 和 数据库 选项 API 版本控制 源 ...
- 编写第一个GET、POST接口[renren-fast框架系列(1)]
配置好 renren-fast 脚手架,学习完 Spring MVC 架构后,我需要具体调试 renren-fast 的接口,比如要新增某个接口. 什么是前后端分离 运行 renren-fast 项目 ...
- jmeter(二十八)利用beanshell进行多重断言
在接口测试中,我们对返回结果的正确性判断一般是基于响应报文的返回内容进行断言.但有些时候,按照正常的业务逻辑来说,一个请求返回的内容是多种不同的. 比如:用户注册功能,注册成功是正常的返回messag ...
- tensorflow源码解析之distributed_runtime
本篇主要介绍TF的分布式运行时的基本概念.为了对TF的分布式运行机制有一个大致的了解,我们先结合/tensorflow/core/protobuf中的文件给出对TF分布式集群的初步理解,然后介绍/te ...
- vue-cli项目创建步骤
vue-cli项目创建步骤: 1.cmd打开命令行窗口 2.输入cnpm install vue-cli -g,然后回车等待(想在哪个目录建立vue项目就要在进入到对应目录再输入命令) 3.安装结束后 ...
- 基于python 实现冒泡排序算法
#!/usr/bin/env python # -*- coding: utf-8 -*- # @Time : 2018/11/17 14:42 # @Author : gylhaut # @Site ...
- 字节跳动流式数据集成基于Flink Checkpoint两阶段提交的实践和优化
背景 字节跳动开发套件数据集成团队(DTS ,Data Transmission Service)在字节跳动内基于 Flink 实现了流批一体的数据集成服务.其中一个典型场景是 Kafka/ByteM ...