决策树（DecisionTree）(附源码)

决策树（DecisionTree）

 

决策树所属类别：监督学习，分类

优点：直观易懂，算法简单

缺点：容易过拟合，对连续型数据不太容易实现

实现方案：ID3，CART，C4.5

详细的资料见连接：别人写的很详细的决策树

这篇博客主要把重点放在决策树程序的实现上，也仅实现了ID3算法，对其他两个算法仅作简单介绍

1.决策数相关知识

1.1数据不纯度

信息熵和基尼系数都是用来评价数据的不纯度的,数据越分散，其不纯度越高，可知当所有数据都相同时其不纯度最低，当所有数据都不同时，其不纯度最高。

信息熵：

假设一个变量的取值有n个：$\begin{Bmatrix} x_{1},x_{2},x_{3},\cdots x_{n} \end{Bmatrix}$，x值对应取到的概率为$\begin{Bmatrix} p_{1},p_{2},p_{3},\cdots p_{n} \end{Bmatrix}$，那么信息熵为：

$Entropy(x)=-\sum_{i=1}^{n}p_{i}log_{2}(p_{i})\\$

可以看出，变量取值的个数越多的数据信息熵越大，数据分布的越平均，信息熵越大；熵越大说明其数据纯度越低。

实际工作中，使用经验熵作为实际计算方法；经验熵里认为变量的极大似然概率等同于变量出现的概率。

经验熵：

假定D表示所有数据的集合，$\left \| D \right \|$表示集合中数据的个数；n表示D中数据种类的个数，$ D_{i} $表示第i个种类的数据集合，$\left \| D_{i} \right \|$表示第i个种类的数据个数；那么下经验熵公式则为：

$Entropy(D) = -\sum_{i=1}^{n}\frac{\left \| D_{i} \right \|}{\left \| D \right \|}log_{2}(\frac{\left \| D_{i} \right \|}{\left \| D \right \|})\\$

基尼系数：

基尼系数与熵比较类似，不过二者的计算方式略有不同；在实际中基尼系数通常会生成与熵非常类似的结果，基尼系数表达式为：

$Gini(D)=-\sum_{i=1}^{n}p_{i}(1-p_{i})=1-\sum_{i=1}^{n}p_{i}^{2}\\$

特性与信息熵很类似。

1.2信息增益

信息增益量：

了解信息增益需要线熟悉条件熵，条件熵是指在已知所有数据D中的某一个特征A的分布后的信息熵，类似于条件概率。

假定特征A有$n_{A}$个取值，根据每一个取值将原始数据D划分为$n_{A}个子集，$D_{i}^{A}$表示表示特征A取第i个指时的子集，$\left \| D_{i}^{A} \right \|$表示子集中数据的个数；那么条件熵为：

$Entropy(D|A)=-\sum_{i=1}^{n_{A}}\frac{\left \| D_{i}^{A} \right \|}{\left \| D \right \|}Entropy(D_{i}^{A})\\$

信息增益是指原始数据的熵减去数据的条件熵，这个值越大表名数据被提纯的越高。

$InfoGain(A) = Entropy(D) - Entropy(D|A)\\$

信息增益率：

信息增益量虽然比较客观，但是有一个问题，就是算法会优先选择特征取值比较多的特征作为分支对象，因为特征取值越多，数据被划分的越细，很容易获得高纯度；为解决这个问题，后来引入了信息增益率，用比例而不是单纯的量作为选择分支的标准。

信息增益率通过引入一个被称作分裂信息（Split Information）的项，来惩罚取值可能性较多的特征。

$SplitInfo(A) = -\sum_{i=1}^{n_{A}}\frac{\left \| D_{i}^{A} \right \|}{\left \| D \right \|}log(\frac{\left \| D_{i}^{A} \right \|}{\left \| D \right \|})\\$

信息增益率即为这两者的比值：

$GainRation(A)=\frac{InfoGain(A)}{SplitInfo(A)}\\$

信息增益率越大，说明使用此特征提纯数据效果越好。

2.决策树创建过程

2.1ID3算法创建过程

这里使用ID3算法演示决策树的创建过程，重点放在算法的构造上，ID3的算法流程如下：

初始化；输入训练数据集D，特征集A，信息增益阈值$\varepsilon $，空决策树T；

1)若D中所有数据同属一个种类$C_{k}$，则决策树T为单节点数，类$C_{k}$为树的类标记，返回T；

2）若$A=\phi $空集，则T为单节点数，将数据中实例最多的类$C_{k}$作为树的类标记，返回T；

3）否则，计算A中所有特征对D的信息增益量（1.2节），选取信息增益量最大的特征$A_{g}$作为节点的特征；

4）如果$A_{g}$的信息增益量小于阈值$\varepsilon $，则置决策树T为单节点数，将数据中实例最多的类$C_{k}$作为树的类标记，返回T；

5）否则对$A_{g}$的每一个可能值$a_{i}$，依$A_{g}=a_{i}$将D分割为若干非空子集$D_{i}^{A}$，并使用$A_{g}=a_{i}$和$D_{i}^{A}$建立T的子节点；

6）再对子结点递归地调用从1）开始的方法。

最终得到一棵决策树。

2.2 python实现决策树算法中的一些函数

信息熵计算：

import numpy as np
#计算样本的信息熵(经验熵)
def calcEntropy(data):
    '''
    输入：
        data: array
            样本数据，data数据中的最后一列代表样本的类别
    返回:
        float
            样本的信息熵
    '''
    sample_size = data.shape[0]
    label_list = list(data[:,-1])

    entropy = 0.0
    for label in set(label_list):
        prob = float(label_list.count(label) / sample_size)
        entropy -= prob * np.log2(prob)

    return entropy 

if __name__ == '__main__':
    test_data = np.array([
        [1,1,1,'YES'],
        [1,1,2,'YES'],
        [1,2,1,'YES'],
        [2,1,1,'YES'],
        [1,2,2,'NO'],
        [2,1,2,'NO'],
        [2,2,1,'NO'],
        [2,2,2,'NO']])
    print(calcEntropy(test_data))

结果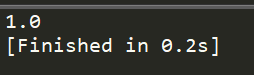

条件熵：

#计算条件熵
def calcConditionalEntropy(data,row):
    '''
    输入：
    data: array
            样本数据，data数据中的最后一列代表样本的类别
        row:int
            选中的特征所处的列号
    返回：
        float
            条件熵的数值
    '''
    length = data.shape[0]
    feature_list = list(data[:,row])

    conditional_entropy = 0.0
    for feature in set(feature_list):
        temp_data = data[data[:,row] == feature]
        prob = len(temp_data)/length

        conditional_entropy += prob*calcEntropy(temp_data)

    return conditional_entropy

if __name__ == '__main__':
    test_data = np.array([
        [1,1,1,'YES'],
        [1,1,2,'YES'],
        [1,2,1,'YES'],
        [2,1,1,'YES'],
        [1,2,2,'NO'],
        [2,1,2,'NO'],
        [2,2,1,'NO'],
        [2,2,2,'NO']])
    print(calcConditionalEntropy(test_data,1))

结果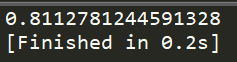

此处不一一举例了，完整的python实现ID3的程序见：Github地址

3.决策树剪枝

决策树生成算法递归的产生决策树，直到不能继续下去为止，这样产生的树往往对训练数据的分类很准确，但对未知测试数据的分类缺没有那么精确，即会出现过拟合现象。过拟合产生的原因在于在学习时过多的考虑如何提高对训练数据的正确分类，从而构建出过于复杂的决策树，解决方法是考虑决策树的复杂度，对已经生成的树进行简化。

决策数剪枝分为：

1）先剪枝（局部剪枝）：在构造过程中，当某个节点满足剪枝条件，则直接停止此分支的构造；

2）后剪枝（全局剪枝）：先构造完成完整的决策树，再通过某些条件遍历树进行剪枝。

决策树剪枝可以简化模型，防止过拟合，提高算法的泛化性能，这里简单介绍一下后剪枝方法。

后剪枝实现方式：极小化决策树整体的代价函数

代价函数：$C_{\alpha }(T) = C(T)+\alpha\left | T \right |$

$C(T)$:模型对训练数据的预测误差

$\left | T \right |$:这棵树的叶子节点

$\alpha$:参数$\alpha>=0$控制两者之间的影响，较大的$\alpha$促使选择较简单的模型（树），较小的$\alpha$促使选择较复杂的模型（树），$\alpha=0$意味着只考虑模型与训练数据的拟合程度，不考虑模型的复杂度。

具体的剪枝实施过程如下：

1）遍历决策树T所有叶子节点；

2）选中一个叶子节点，使其父节点将所有叶子节点回缩，让父节点变为叶子节点，回缩后的数记为$T_{b}$；

3）计算原数T的代价函数$C(T)$与回缩后数$T_{b}$的代价函数$C(T_{b})$,若$C(T) > C(T_{b})$，则$T_{b}$为新的树，否则依旧以$C(T)$为树；

4）按照以上步骤对所有叶子节点进行测试，直到没有叶子节点进行回缩为结束。