vs 2015 插件 supercharger 破解方式
亲测有效:效果如图
方法如下:
1、打开Supercharger的options;
2、点击Pricing & Registration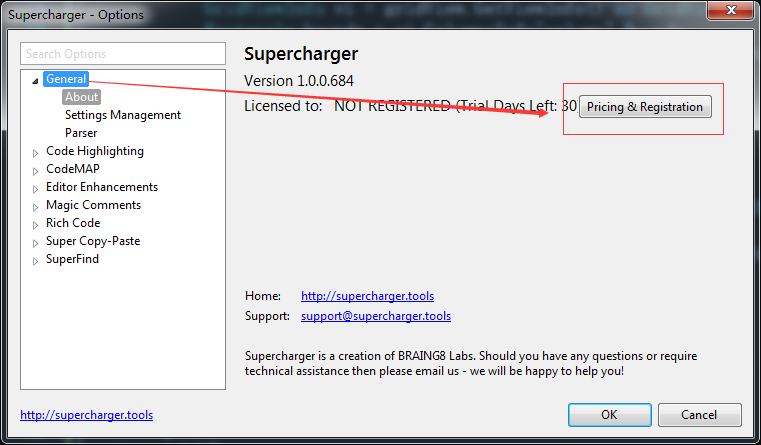
3、复制 license 然后再按Paste & Use License Key;
tt4e2HN4X3gEhlQm2a0qCFCNM3PMTVcFUD8q7POTX3GaJpTmrUx/Z2cOufl+pyZIsB1QLtzlYYqcB739vTKP1G2sEYTw/cCegh1xpHYE2Cp4CvRc/N95/bQTPjLyajOLUJ0iHvUDj2A
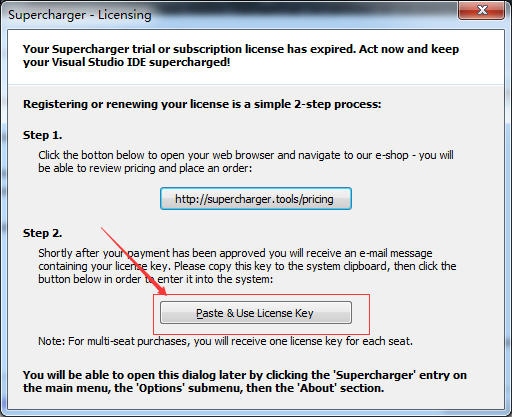
点击后结果:
4、找到C:\Windows\System32\Drivers\etc下 的hosts 文件,用记事本打开编辑,将
127.0.0.1 supercharger.tools 黏贴到下图所示位置即可,保存关闭,重启vs。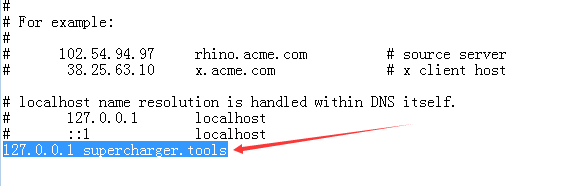
5、重启vs后再次打开Options,若是下图显示,则说明破解成功。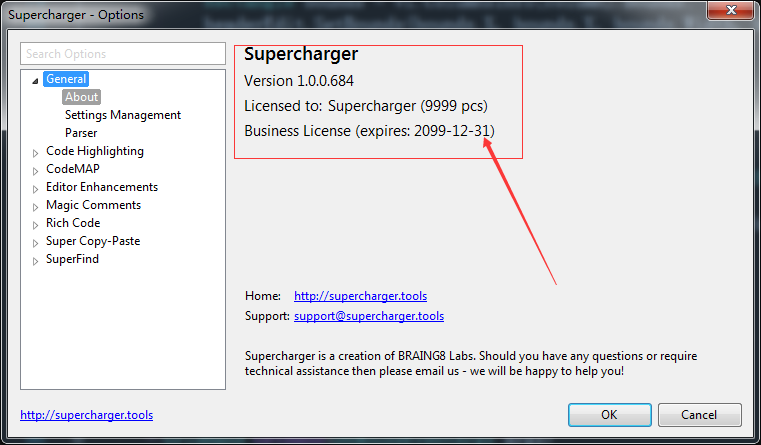
原作地址:http://blog.csdn.net/u012097590/article/details/53006904
vs 2015 插件 supercharger 破解方式的更多相关文章
- VS增加插件 Supercharger破解教程
VS增加插件 Supercharger破解教程 Supercharger效果预览及下载路径: http://supercharger.tools/index.html 下载地址:https://vis ...
- VS增强插件 Supercharger破解教程
Supercharger 破解教程:步骤:1.打开Supercharger的options; 2.点击Pricing & Registration 3.复制 license tt4e2HN4X ...
- VS Supercharger插件的破解
Supercharger我已经用了很多年了,感觉十分不错,最初使用的时候,是叫做CodeMap.不过要想很好的使用起来这个VS插件,需要对其进行细致的设置. 这里不再多说了,看下,这个软件怎么破解吧. ...
- [Android Studio]SQLScout插件安装破解
以下内容为原创,欢迎转载,转载请注明 来自天天博客:http://www.cnblogs.com/tiantianbyconan/p/5972138.html [Android Studio]SQLS ...
- 【MyEclipse 2015】 逆向破解实录系列【终】(纯研究)
声明 My Eclipse 2015 程序版权为Genuitec, L.L.C所有. My Eclipse 2015 的注册码.激活码等授权为Genuitec, L.L.C及其付费用户所有. 本文只从 ...
- 【MyEclipse 2015】 逆向破解实录系列【2】(纯研究)
声明 My Eclipse 2015 程序版权为Genuitec, L.L.C所有. My Eclipse 2015 的注册码.激活码等授权为Genuitec, L.L.C及其付费用户所有. 本文只从 ...
- Adobe Acrobat XI Pro 两种破解方式 Keygen秘钥 license替换 亲测有效
大家平时看paper比较多的话想必都是用Adobe Acrobat而非Adobe Reader吧,其功能全面之处就不啰嗦了,下面给大家分享下Adobe Acrobat XI Pro的两种破解方式(两种 ...
- vim插件的安装方式 -- vim注释插件和doxygen函数注释生成插件-ctrlp插件-tabular等号对齐 插件
使用unzip的时候 指定 -d选项, 是说明解压到的 目标地址. 这个参数还是比较方便的, 比直接unzip到当前目录, 然后在去拷贝到目标目录, 然后再删除当前目录中的解压文件夹, 方便多了. 使 ...
- Android动态方式破解apk终极篇(加固apk破解方式)
一.前言 今天总算迎来了破解系列的最后一篇文章了,之前的两篇文章分别为: 第一篇:如何使用Eclipse动态调试smali源码 第二篇:如何使用IDA动态调试SO文件 现在要说的就是最后一篇了,如何应 ...
随机推荐
- html5 拖拽练习题
html5新的拖拽 只支持Internet Explorer 9.Firefox.Opera 12.Chrome 以及 Safari 5 支持拖放. 来一个实例: <!DOCTYPE html& ...
- Spring Boot 运行原理
Spring Boot并没有任何新的技术,全都是基于Spring4提供的技术,用优秀的设计,为Web开发提供了一套新的方式. 在HelloWorld中,我们没有进行任何显示的配置,但是程序还是运行起来 ...
- Openstack keystone组件详解
OpenStack Keystone Keystone(OpenStack Identity Service)是 OpenStack 框架中负责管理身份验证.服务规则和服务令牌功能的模块.用户访问资源 ...
- 《高性能MySQL》 读书总结
目录: 第一章.MySQL架构与历史 第二章.MySQL基准测试 第三章.服务器性能剖析 第四章.Schema与数据类型优化 第五章.创建高性能的索引 第六章.查询性能优化 第七章.MySQL高级特性 ...
- Socket_SSH-2(大文件的一次传输)
import socket,os server=socket.socket() server.bind(('localhost',9999)) server.listen() while True: ...
- JSON字符串和Javascript对象字面量
JSON字符串和Javascript对象字面量 JSON是基于Javascript语法的一个子集而创建的,特别是对象和数组字面量语法. 正是由于JSON的这种特殊来历,导致很多Javascript程序 ...
- [POI2014]DOO-Around the world
通过几年的努力,Byteasar最终拿到了飞行员驾驶证.为了庆祝这一事实,他打算买一架飞机并且绕Byteotia星球赤道飞行一圈.但不幸的是赤道非常长所以需要中途加几次油.现在已知赤道上面所有飞机场, ...
- Leetcode 200. 岛屿的个数(扩展)
1.题目描述 给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量.一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的.你可以假设网格的四个边均被水包围. 示例 ...
- Linux(CentOS6.7) 安装MySql5.7数据库 图文教程
linux(CentOS6.7) 环境Mysql 5.7.17安装教程分享给大家,供大家参考,具体内容如下: 1系统约定安装文件下载目录:/data/softwareMysql目录安装位置:/usr/ ...
- eclipse如何远程debug/断开远程debug
eclipse如何远程debug? 当你的代码已经部署到生产或者测试环境的时候,你如何debug判断线上的问题呢? debug之前必须保证本地代码和远程代码完全一致,否则将不能建立连接 在eclips ...

