（原创）Stanford Machine Learning (by Andrew NG) --- (week 8) Clustering & Dimensionality Reduction

本周主要介绍了聚类算法和特征降维方法，聚类算法包括K-means的相关概念、优化目标、聚类中心等内容；特征降维包括降维的缘由、算法描述、压缩重建等内容。coursera上面Andrew NG的Machine learning课程地址为：https://www.coursera.org/course/ml

 （一）K-means聚类算法

Input data：未标记的数据集，类别数K；

算法流程：

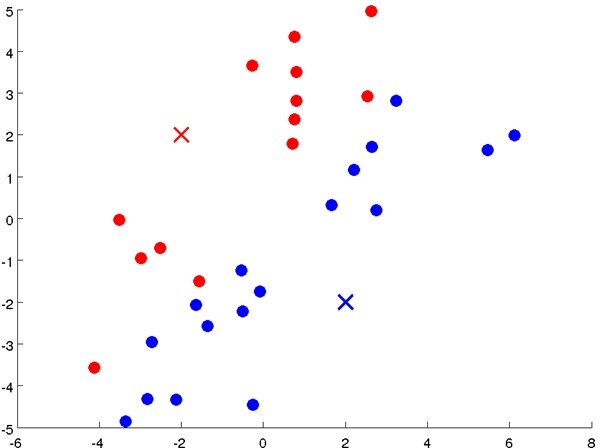
• 首先随机选择K个点，作为初始聚类中心（cluster centroids）；
• 计算数据集中每个数据与聚类中心的距离，将其划分到与其最近的中心点那类；
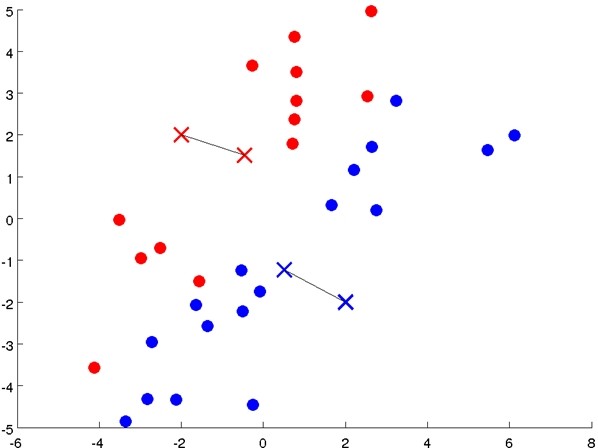
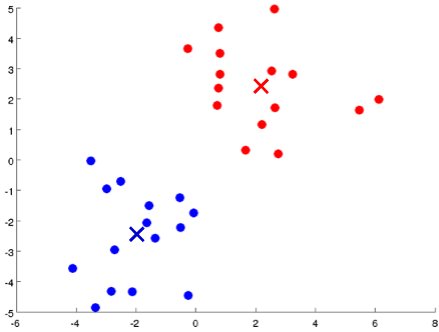
• 重新计算每个类的平均值，并将其作为新的聚类中心；
• 重复步骤2-4直至聚类中心不再变化；

正如下图所示的迭代过程：

算法伪代码：

随机初始化K个聚类中心，用μ₁,μ₂,...,μ_k表示，c⁽¹⁾,c⁽²⁾,...,c^(m)表示第i个样本最近的聚类中心：

Repeat {

　　for i = 1 to m

    　　c⁽ⁱ⁾:= index (from 1 to K) of cluster centroid closest to x⁽ⁱ⁾

  　 for k = 1 to K

    　　 μ^k:= average (mean) of points assigned to cluster k}

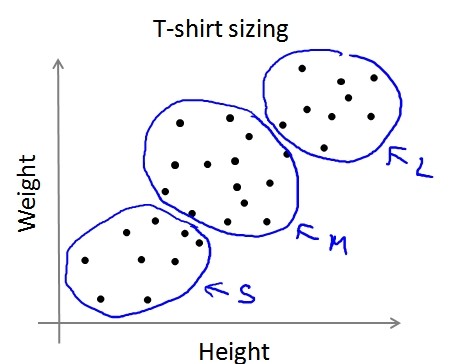
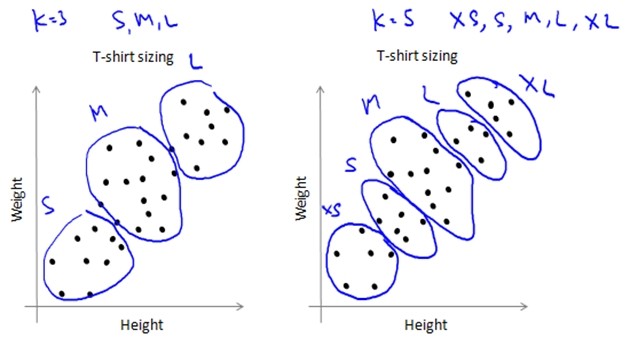
PS:K-means算法也可以用于在没有明显区分的情况下将数据分组，如T-shirt的尺寸问题。

---

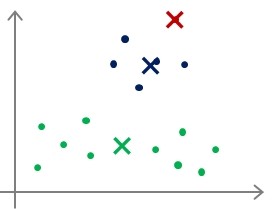
优化目标（Optimization objective）

Goal：  

即最小化所有的样本点与其最近的聚类中心点之间的距离之和。

 其中

•第一个循环是用于减小c(i)引起的代价：选择最短距离；

•第二个循环则是用于减小μi引起的代价：选择聚类中心；

•迭代的过程一定会是每一次迭代都在减小代价函数，不然便是出现了错误；

---

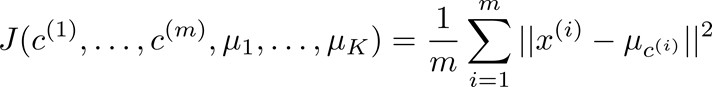
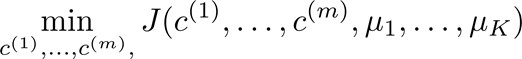
聚类中心初始化（Random initialization）

若初始聚类中心选择不好，会出现局部最优的问题，如下图所示：

初始化聚类中心：

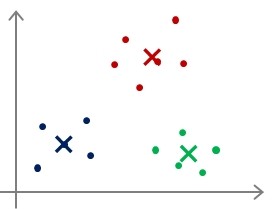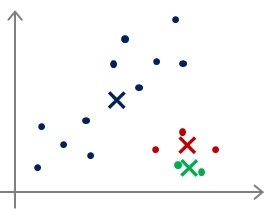• 选择K<m，即聚类中心点的个数要小于所有训练集的数量；
• 随机选择K个训练实例，然后令K个聚类中心分别与这K个训练实例相等；

改善局部最优：

• 多次运行K-means算法，每次都进行随机初始化；
• 计算代价函数，选择代价最小的结果。

PS：对于2≤K≤10，比较可行；过大的K则不会有明显效果。 

---

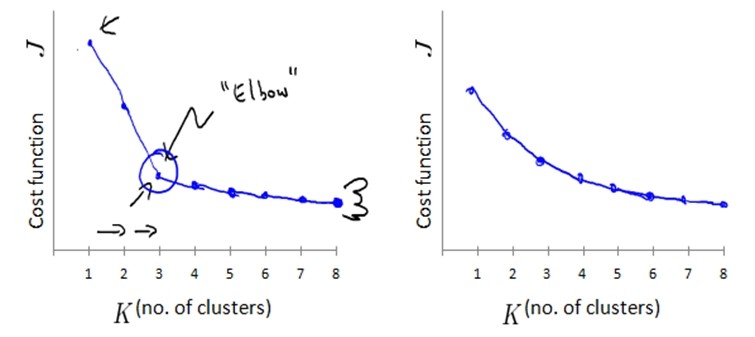
聚类数选择（Choosing the number of clusters）

绘制K与cost function的关系函数，若如左图所示，有明显的“elbow”折点，则选择该点对应的K；但若如右图所示，并未明显折点，则一般会基于实际情况人工的选择K。

如在T-shirt问题上，我们可以分成三个号，也可以考虑分成五个号。

---

（二）降维（Dimensionality Reduction）

数据压缩（Data Compression）

1. 2D-1D：面—线

  若对于样本采集到了两种特征，但特征直接有些重复，现在我们可以选择合适的直线，可以将所有样本点投影到该直线上，并使用新的特征来表示原特征的近似。这样我们的算法会有更高的效率。如下图所示：

2. 3D-2D：体—面

   与2D-1D问题类似，我们可以在三维向量投影到二维的面上，从而实现降维。如下图所示：

同理，我们可以将更多维度的特征降低。

---

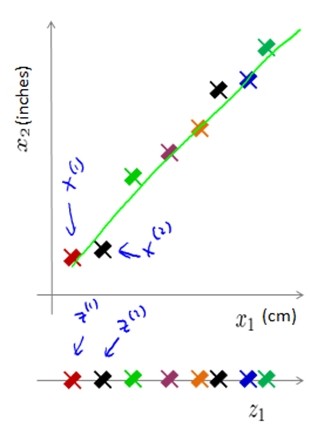
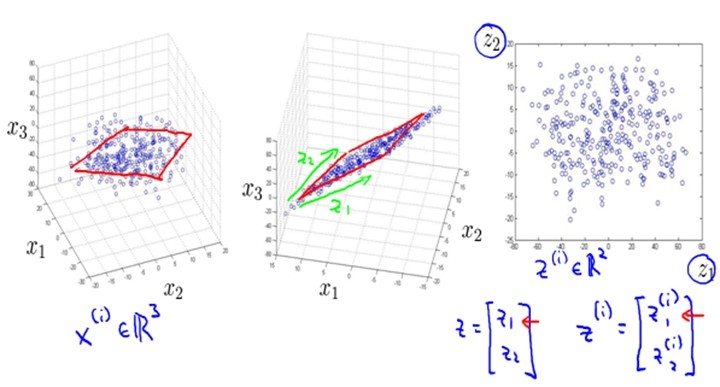
数据可视化（Data Visualization）

  假设我们有一些国家的相关数据（如下表所示），每个样本表示一个国家，每个国家有50维特征，通过使用降维的方法可以将样本数据可视化，即降至三维及以下可画图的维度。

假设，我们将这50维特征降成了两维（左），画图（右）：

---

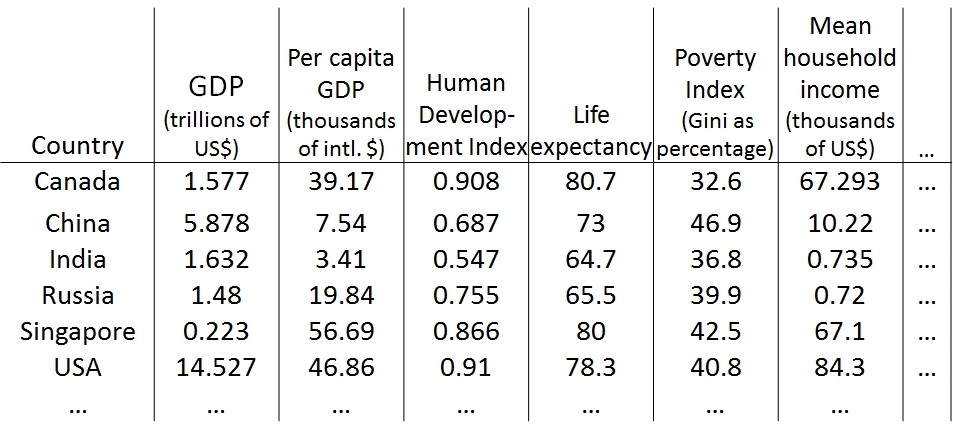
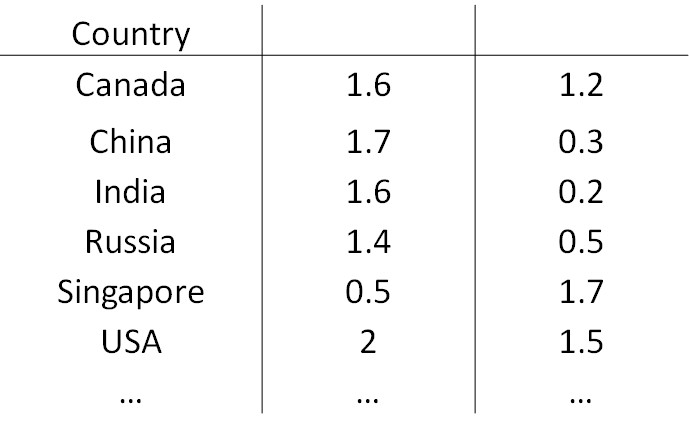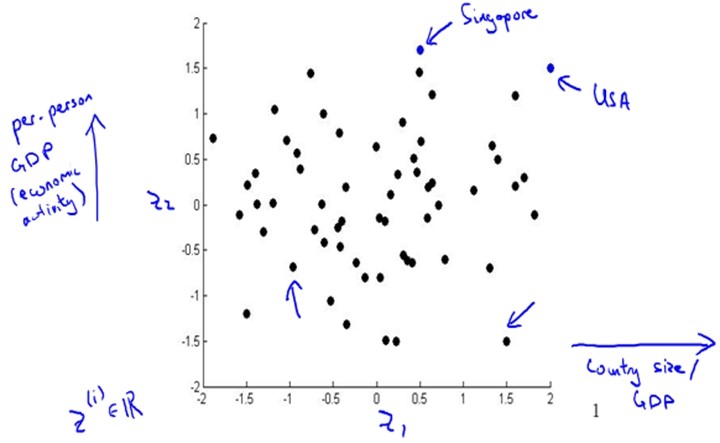PCA（Principal Component Analysis ）

PCA是常见的降维算法，可以将n维数据降至k维。

目标：找到向量u⁽¹⁾,u⁽²⁾,...,u^(k)使得投射误差最小；

PCA vs 线性回归

PCA	Linear Regression
投影误差最小（右图）	预测误差最小（左图）
无预测任务	需预测结果

---

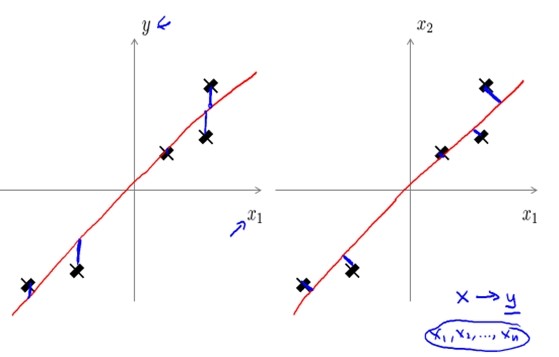
PCA算法

1. 预处理：均值归一化，计算所有特征均值μ_j,令x_j=x_j-μ_j；

其中

2. 计算协方差矩阵；

3. 计算协方差矩阵的特征向量：使用svd函数；

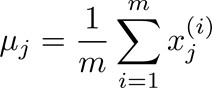
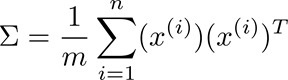
[U,S,V] = svd(Sigma);

其中U是最小投影误差的方向向量构成的矩阵。

4. 降维：得到矩阵U后，我们可以选择前K个向量，得到n*K维矩阵，用U_reduce表示，用下面的算式计算新的特征向量z⁽ⁱ⁾；

U_reduce = U(:,1:k);

z = U^T_reduce *x;

---

压缩重建& k的选择

1. 压缩重建：

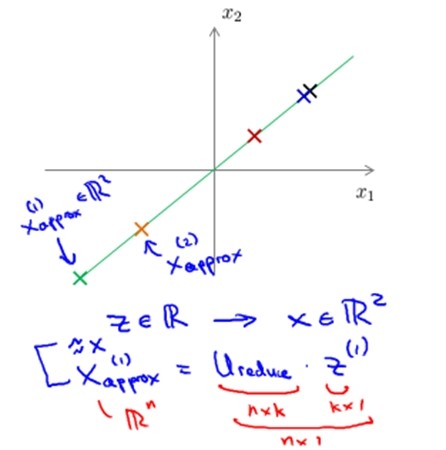
• 通过z = U^T_reduce *x计算特征向量z；其中x是n*1维，所以z是k*1维。
• 通过x_approx = U^T_reduce * z来近似得到原来的特征向量x；其中z是k*1。所以x_approx 是n*1维。

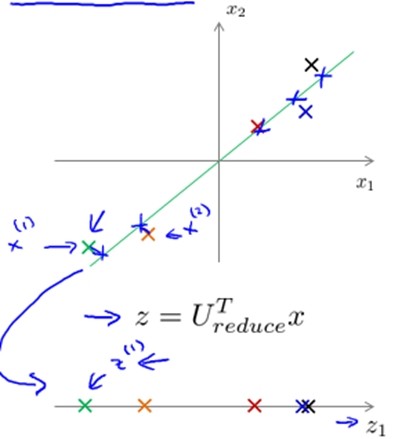从上面的分析中可以看出，我们希望在误差尽量小的情况下k值尽量小，那么怎样选择k呢？

2. 方法一：

• 在k = 1时，使用PCA算法；
• 计算U_reduce,z⁽¹⁾_,z⁽²⁾,...,z^(m),x⁽¹⁾_approx ,...,x^(m)_approx
• 检验是否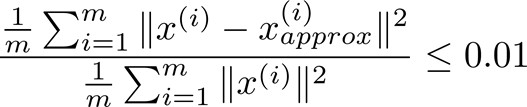？若否，则继续尝试k=2，k=3，.......

3. 方法二：

在Octave中使用svd函数时，[U,S,V] = svd(Sigma);其中的S是n*n的矩阵，只有对角线上有值，如下所示：

 ≡  

---

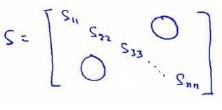
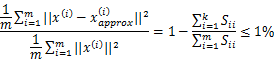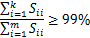
使用PCA的优势及应用

假如我们的输入特征向量是10000维，在使用PCA后可以降至1000维，这样可以加速训练过程，并减少内存。

PS：对于测试集和交叉验证集,同样可以使用训练集得到的U_reduce.由于我们将特征空间由n维减少到了k维，有人会认为这样做会避免过拟合，这样做也许有效，但不是很好的避免过拟合的方法。若要避免过拟合，还是应尝试正则化的方法。

---

HOMEWORK

好了，既然看完了视频课程，就来做一下作业吧，下面是Clustering & Dimensionality Reduction部分作业的核心代码：

1. findClosestCentroids

m = size(X,1);
dis_vec = zeros(K,1);
for i = 1:m
    for j = 1:K
        dis_vec(j) = sum((X(i,:)-centroids(j,:)).^2);
    end
    [v,k] = min(dis_vec);
    idx(i) = k;
end

2. computeCentroids

 tp_sum = zeros(K, n);
 tp_num = zeros(K, 1);
 for i = 1:m
     cy = idx(i);
     tp_sum(cy,:) = tp_sum(cy,:) + X(i,:);
     tp_num(cy) += 1;
 end
 for j = 1:K
     centroids(j,:) = tp_sum(j,:)/tp_num(j);
 end

3. pca.m

sigma = (1/m)*X'*X;
[U,S,V] = svd(sigma);

4. projectData.m

Z = X*U(:,1:K);

5. recoverData.m

X_rec =  Z* U(:,1:K)';