[CODE FESTIVAL 2017]Full Tournament

题意：$2^n$个编号为$1\cdots2^n$的人打比赛，这个比赛会给每个人一个唯一的排名，比赛规则递归地定义如下：

$2^n$个人打的是级别为$n$的比赛，初始时他们按某种顺序站成一排

当$n=0$，唯一的一人是第一名

当$n\geq1$，每相邻两个人PK，编号小的人获胜，让$2^{n-1}$个胜者按在原序列中的相对顺序进行级别为$n-1$的比赛，让$2^{n-1}$个败者按在原序列中的相对顺序进行级别为$n-1$的比赛，并将他们的排名加上$2^{n-1}$

可以看出如果初始时的顺序确定了，这样一定可以给所有人一个唯一的排名

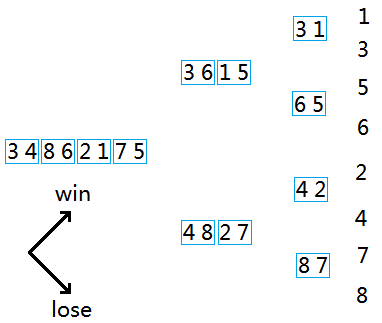
题意不是特别易懂，上图描述了一个打比赛的过程

现在给定一份最终每个人的排名，有一些人的排名还未确定，让你构造一个初始序列使得最终排名和输入相符

以下用从$0$开始的下标和排名

首先，我们可以通过合理安排顺序，使得每次PK都是左边的人赢，考虑把打比赛的过程倒序，那么两个在$n-1$级比赛中排名都为$i$的人会进行一次PK，胜者在$n$级比赛中的排名为$2i$，败者为$2i+1$

然后有一个判定是否有解的结论：如果在一场级别为$n$的比赛中第$i$名的人是$a_i$，那么$a_i\lt a_{i+2^j}(i\&2^j=0,0\leq j\lt n)$

考虑用归纳法证明：当$j=0$时显然成立（这是许多场$1$级比赛），设当$j\lt n-1$时结论成立

若$i=2k$，那么$i$是两个在$n-1$级比赛中排名都为$k$的人之间的PK胜者，$i+2^{n-1}$是两个在$n-1$级比赛中排名都为$k+2^{n-2}$的人之间的PK胜者，因为两个$n-1$级比赛中都有$a_k\lt a_{k+2^{n-2}}$，所以$i$是四个人中最强的，也就是说$a_i\lt a_{i+2^{n-1}}$

若$i=2k+1$，类似可得$i+2^{n-1}$是最弱的，所以结论成立

有了这个结论，问题转为：给定一个DAG$i\rightarrow i+2^j(i\&2^j=0)$和部分节点的权值$a_i$，填上剩下的权值使其满足限制$i\rightarrow j,a_i\lt a_j$

首先正反各扫一遍，得到每个节点的权值的取值范围，这是一个区间

直接贪心即可，从小到大依次填数，填$x$时选择未被选择的区间中满足$L\leq x$且有最小$R$的区间，这个直接按$L$从小到大加入区间，用优先队列维护$R$即可

因为每次都是左边的人赢，即按奇偶性分开，所以最后要像FFT一样把$i$的权值放到$rev_i$去

这个题好神啊...

#include<stdio.h>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
int a[262144],rev[262144],lw[262144],hi[262144],val[262144];
struct pr{
	int x,y;
	pr(int a=0,int b=0){x=a;y=b;}
};
bool operator<(pr a,pr b){return a.x==b.x?a.y>b.y:a.x>b.x;}
priority_queue<pr>q;
vector<pr>e[262144];
int main(){
	int n,N,i,j;
	scanf("%d",&n);
	N=1<<n;
	for(i=0;i<N;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(n-1));
	for(i=0;i<N;i++){
		scanf("%d",a+i);
		a[i]--;
	}
	for(i=N-1;i>=0;i--){
		hi[i]=~a[i]?a[i]:N-1;
		for(j=0;j<n;j++){
			if(~i>>j&1)hi[i]=min(hi[i],hi[i|(1<<j)]);
		}
	}
	for(i=0;i<N;i++){
		lw[i]=~a[i]?a[i]:0;
		for(j=0;j<n;j++){
			if(i>>j&1)lw[i]=max(lw[i],lw[i^(1<<j)]);
		}
	}
	for(i=0;i<N;i++){
		if(lw[i]>hi[i]){
			puts("NO");
			return 0;
		}
		e[lw[i]].push_back(pr(hi[i],i));
	}
	for(i=0;i<N;i++){
		for(pr t:e[i])q.push(t);
		if(q.empty()||q.top().x<i){
			puts("NO");
			return 0;
		}
		val[q.top().y]=i;
		q.pop();
	}
	puts("YES");
	for(i=0;i<N;i++)printf("%d ",val[rev[i]]+1);
}