Codeforces 500 E. New Year Domino

[$>Codeforces \space 500 E. New Year Domino

题目大意 : 数轴上有序排列着 \(n\) 块多米诺骨牌， 第 \(i\) 块骨牌坐标为 \(p_i\) 长度为 \(l_i\)

如果推倒坐标为 \(p_i\) 的多米诺骨牌，那么区间 \([p_i, p_i + x_i]\) 中的多米诺骨牌都会被推倒，从而发生连锁反应.

现在有 \(q\) 组询问，每次询问之前可以让一些多米诺骨牌增加任意长度，代价是增加的长度之和。

询问的内容是每次推倒第 \(x\) 块骨牌，求要推倒第 \(y\) 块至少要花费的代价 (询问之间相互独立)

\(2 \leq n , q\leq 2 \times 10^5 \ 1 \leq p_i, l_i \leq 10^9\)

解题思路 :

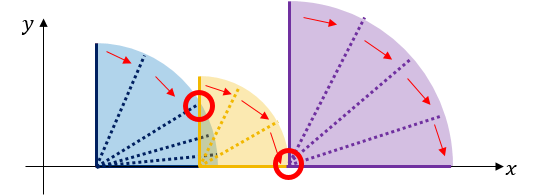
观察发现，多米诺之间的连锁反应可以合并成一个块，每次从右到左每次新加骨牌的时候可以合并被它覆盖的块。

但是直接按照定义合并的话，只能保证一个块最左边的块可以推倒整个块，也就是说一个块的贡献只有在推倒整块最左边的骨牌时是合法的

仔细想了很久觉得并没有什么做法可以在线求出 \(x\) 对应的合法联通块，不妨大胆离线.

离线后按照询问的左端点排序，从右到左扫，边扫边用一个栈维护此时的联通块的状态和联通块之间的距离

对于每一个扫到的 \(i\)，在其合并完之后处理 \(i\) 作为左端点的询问的答案

因为此时 \(i\) 左边的点还没有被加进联通块，所以从 \(i\) 开始推一定是合法的， 对于每一个左端点在 \(i\) 上的询问，算出两个联通块之间的距离就是答案

/*program by mangoyang*/
#include<bits/stdc++.h>
#define inf (0x7f7f7f7f)
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
typedef long long ll;
using namespace std;
template <class T>
inline void read(T &x){
    int f = 0, ch = 0; x = 0;
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
    for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - 48;
    if(f) x = -x;
}
#define int ll
#define N (1000005)
int fa[N], l[N], r[N], st[N], sum[N], Ans[N], n, m, top;
struct Query{ int x, id; }; vector<Query> q[N];
inline int ask(int x){ return x == fa[x] ? x : fa[x] = ask(fa[x]); }
main(){
	read(n);
	for(int i = 1, x, y; i <= n; i++)
		read(x), read(y), l[i] = x, r[i] = x + y;
	for(int i = 1; i <= n; i++) fa[i] = i;
	read(m);
	for(int i = 1, L, R; i <= m; i++)
		read(L), read(R), q[L].push_back((Query){R, i});
	for(int i = n; i >= 1; i--){
		int x = i;
		while(top && l[st[top]] <= r[x]){
			r[x] = Max(r[x], r[st[top]]);
			fa[ask(st[top])] = x, top--;
		}
		if(top) sum[x] = sum[st[top]] + l[st[top]] - r[x];
		st[++top] = x;
		for(int j = 0; j < q[i].size(); j++){
			int id = q[i][j].id, y = q[i][j].x;
			Ans[id] = sum[ask(x)] - sum[ask(y)];
		}
	}
	for(int i = 1; i <= m; i++) printf("%lld\n", Ans[i]);
	return 0;
}