[luoguT30208]太极剑

题面在这里

description

在一个圆环上给出\(n\)条端点在圆环上的绳子，

每次在圆环上切割的轨迹是一条直线，可以将可以将所有与这条直线相交的绳子切断。

求切割次数的最小值。

data range

\[n\le 2\times 10^5
\]

solution

洛谷月赛题目真的棒

某题弱化版

我们记一个圆环的点割为

将每条直线相对应的两个端点染上同种颜色，之后在圆环上选\(2k\)个切割点，使得每两个相邻的切割点之间没有同色点的方案

例如一个\(n=3\)的圆环: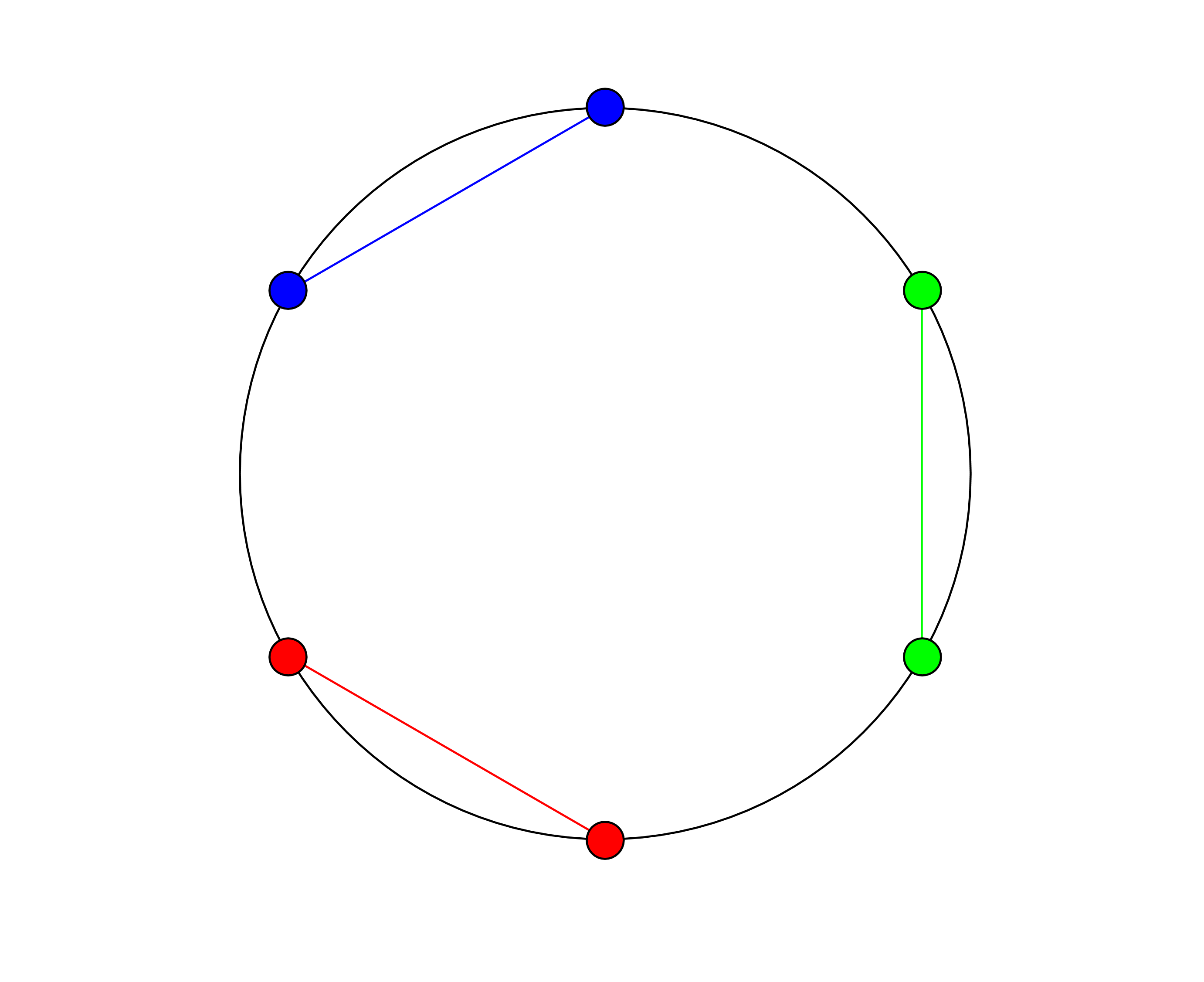

我们能够找到一个对应\(k=2\)的点割的方案为:

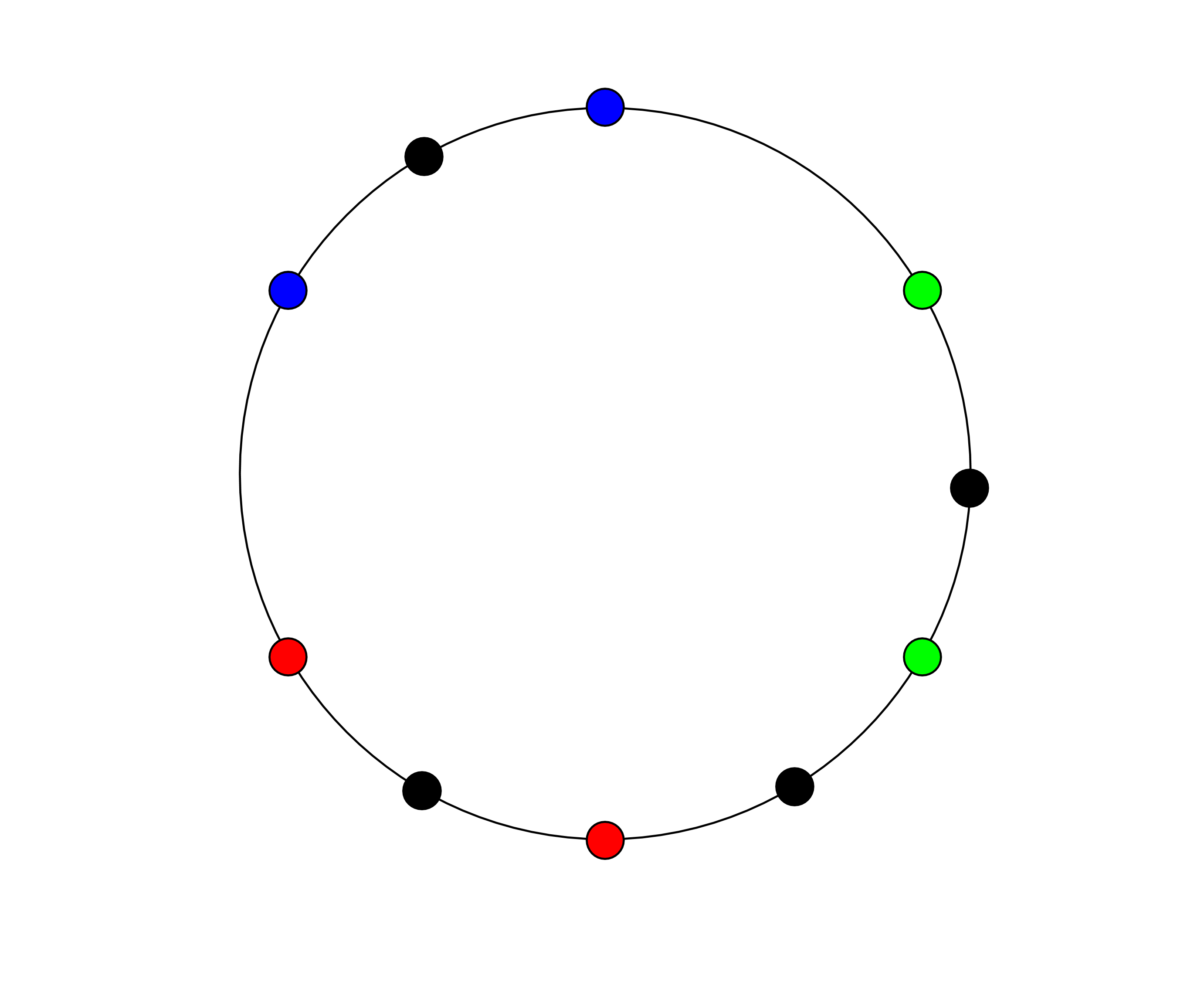
那么我们知道:每个点割都对应着题目中满足要求的一个方案

考虑构造方案，只要将每两个切割点之间的点隔开即可

于是我们每隔\(k\)个点连一条边,就构造出了一个可行的方案:

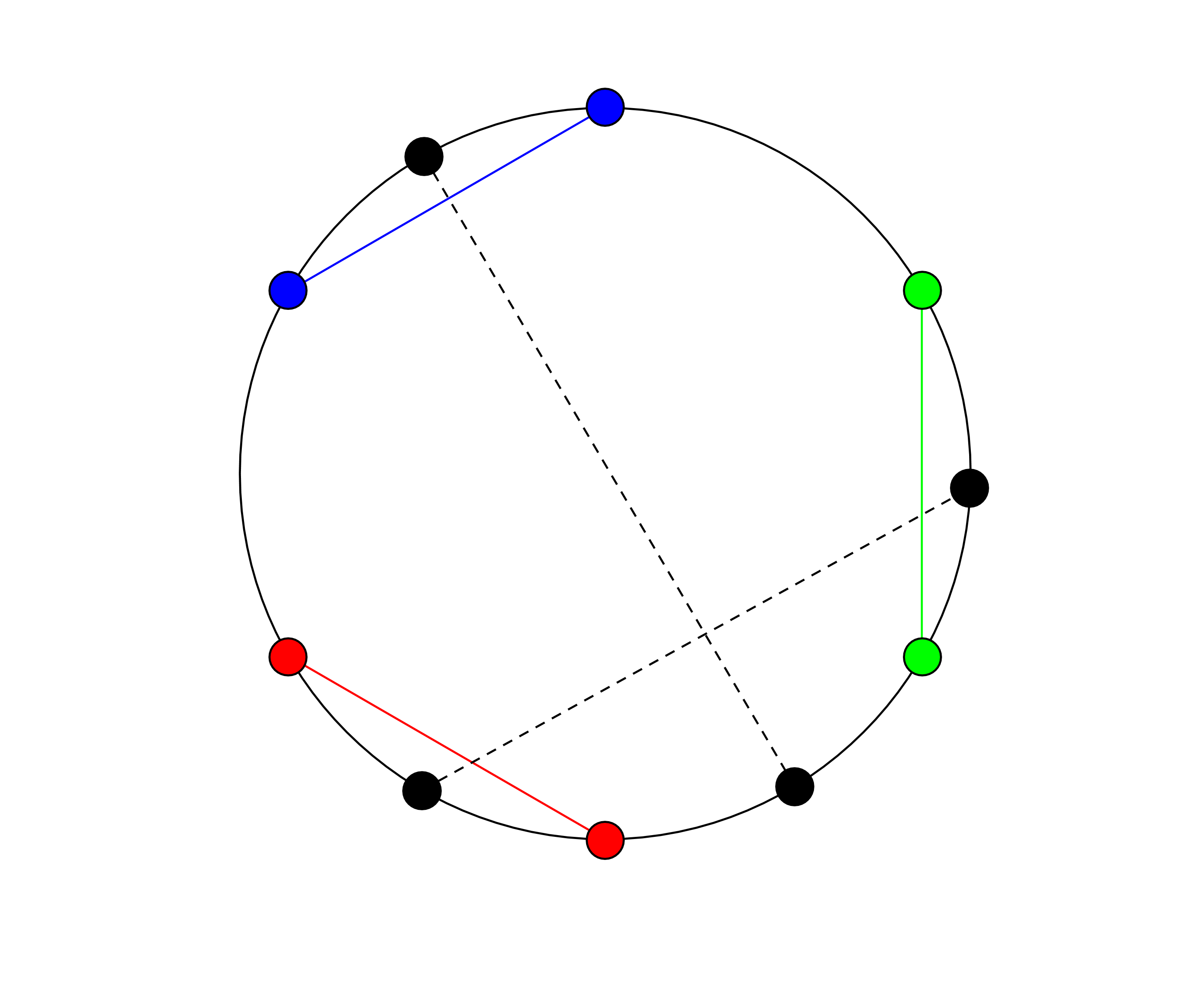
这样我们把题目转化为求一个圆环的最小点割

考虑枚举第一个点的位置，断环为链:



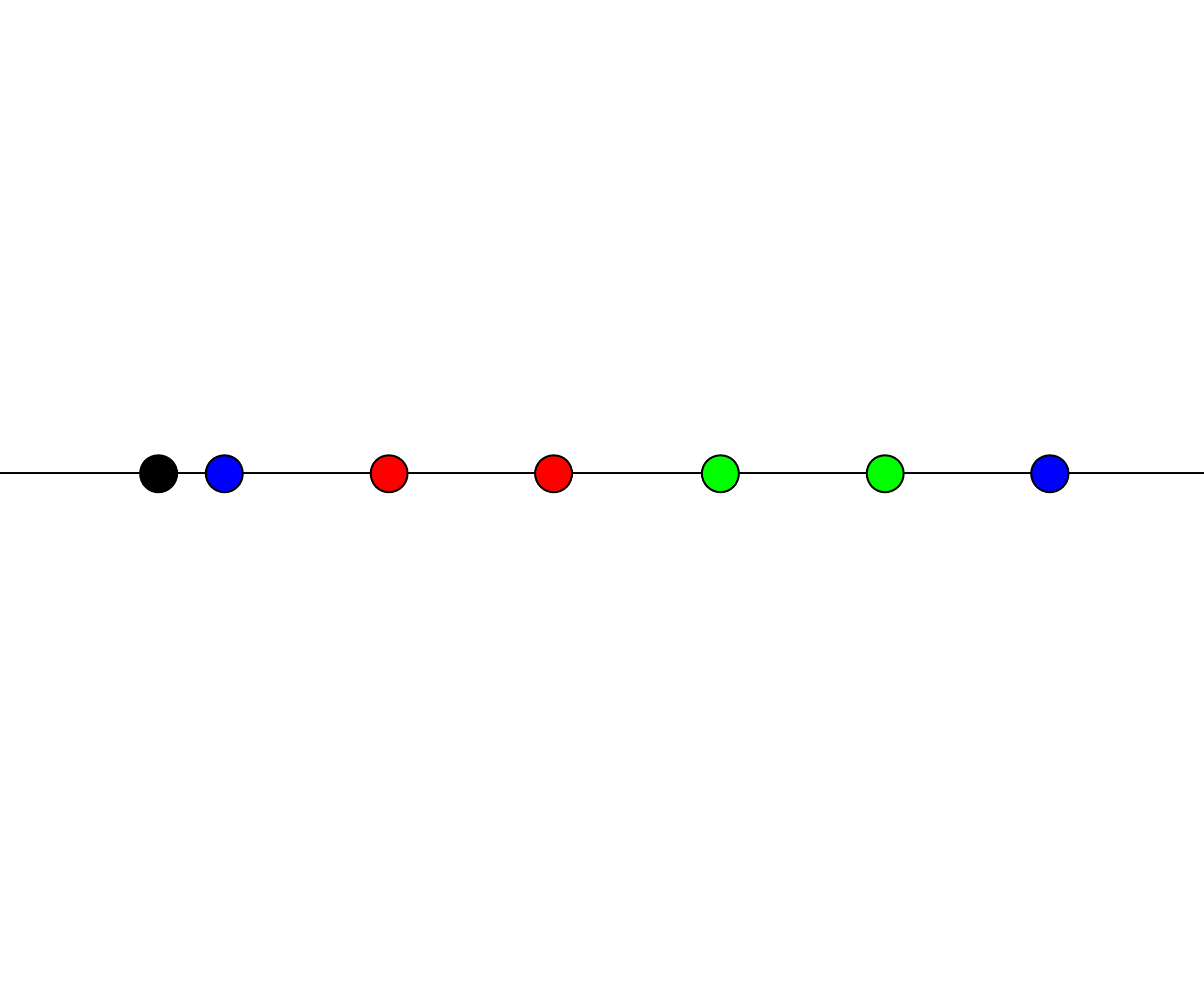
于是我们只要向后贪心，找到其能延伸最远的位置即可：



在找到一个最小点割的同时，我们也找到了一个对应的方案；

如果我们现在直接枚举第一个点的位置，复杂度应该是\(O(n^2)\)的

我们考虑距离最短的一组点对，这组点对之间必然有一个切割点，因此我们只要在这组点对之间枚举切割点即可，假设这组点对的最短距离为\(d\),那么我们每一轮贪心地跳是\(O(n/d)\)的(只要你预处理每个点最远能够延伸的点，每一次跳的长度必然\(\ge d\))，故时间复杂度为\(O(n)\)。

code

#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<iomanip>
#include<cstring>
#include<complex>
#include<vector>
#include<cstdio>
#include<string>
#include<bitset>
#include<ctime>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<set>
#define FILE "a"
#define mp make_pair
#define pb push_back
#define RG register
#define il inline
using namespace std;
typedef unsigned long long ull;
typedef vector<int>VI;
typedef long long ll;
typedef double dd;
const dd eps=1e-10;
const int mod=1e9+7;
const int N=200010;
const int inf=2147483647;
const dd pi=acos(-1);
il ll read(){
	RG ll data=0,w=1;RG char ch=getchar();
	while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
	if(ch=='-')w=-1,ch=getchar();
	while(ch<='9'&&ch>='0')data=data*10+ch-48,ch=getchar();
	return data*w;
}

il void file(){
	freopen(FILE".in","r",stdin);
	freopen(FILE".out","w",stdout);
}

int n,s,c[N<<1],p[N][7],ans=inf;
int nxt[N<<1];
il int dist(int i,int j){return (i<j)?(j-i):(j-i+n);}

il int go(int s){
	RG int cnt=0;
	for(RG int i=s,b=0;!b||i<s;i=nxt[i]){
		cnt++;if(nxt[i]<i)b=1;
	}
	return (cnt+1)/2;
}

int main()
{
	n=read();n<<=1;
	for(RG int i=1,x,y;i<=n/2;i++){
		x=read();y=read();c[x]=c[y]=i;
		if(dist(y,x)<dist(x,y))swap(x,y);p[i][0]=x;p[i][8]=y;
		if(!s||dist(p[s][0],p[s][9])>dist(p[i][0],p[i][10]))s=i;
	}
	nxt[p[s][0]]=p[s][11];
	for(RG int i=(p[s][0]-2+n)%n+1;i!=p[s][0];i=(i-2+n)%n+1){
		nxt[i]=nxt[i%n+1];
		if(i==p[c[i]][0]&&dist(i,nxt[i])>dist(i,p[c[i]][12]))
			nxt[i]=p[c[i]][13];
		if(i==p[c[i]][14]&&dist(i,nxt[i])>dist(i,p[c[i]][0]))
			nxt[i]=p[c[i]][0];
	}
	for(RG int i=p[s][0]%n+1;i!=p[s][15]%n+1;i=i%n+1)ans=min(ans,go(i));
	printf("%d\n",ans);
	return 0;
}