持续集成之配置环境创建JOB
1、安装mvn、gitlab插件
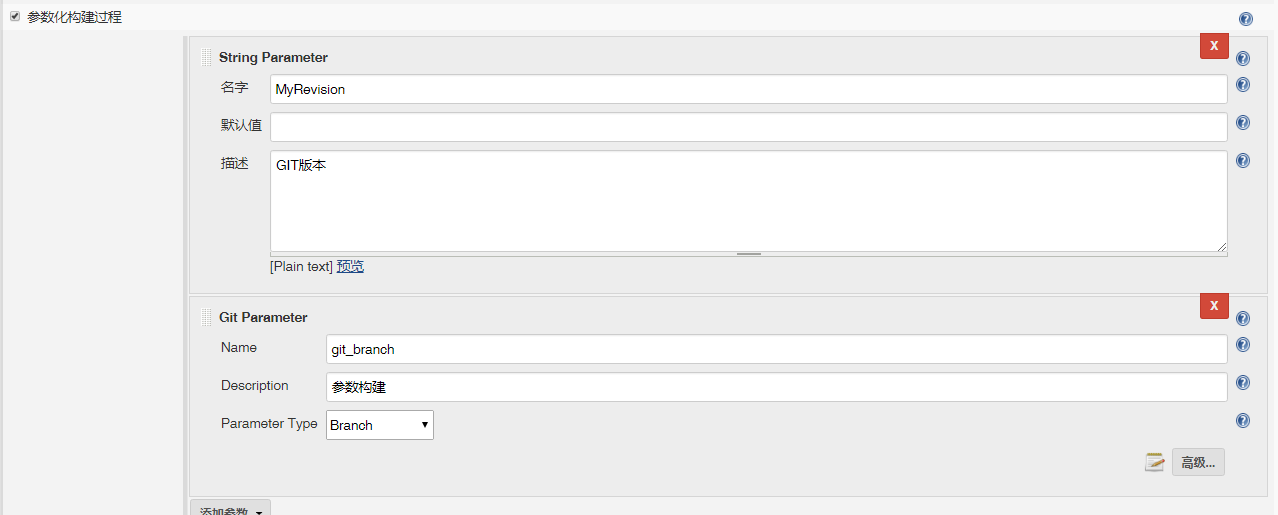
2、配置参数构建
持续集成之配置环境创建JOB的更多相关文章
- Jenkins持续集成学习-Windows环境进行.Net开发1
目录 Jenkins持续集成学习-Windows环境进行.Net开发 目录 前言 目标 使用Jenkins 安装 添加.net环境配置 部署 结语 参考文档 Jenkins持续集成学习-Windows ...
- Jenkins持续集成学习-Windows环境进行.Net开发2
目录 Jenkins持续集成学习-Windows环境进行.Net开发2 目录 前言 目标 使用 .Net Stardard 单元测试 流程 手动执行单元测试 自动执行单元测试 单元测试报告 上传Nug ...
- Jenkins持续集成学习-Windows环境进行.Net开发3
目录 Jenkins持续集成学习-Windows环境进行.Net开发3 目录 前言 目标 优化nuget包生成流程 自动触发构建 Jenkins定时轮询触发 SVN客户端钩子触发 SVN服务器钩子触发 ...
- Jenkins持续集成学习-Windows环境进行.Net开发4
目录 Jenkins持续集成学习-Windows环境进行.Net开发4 目录 前言 目标 Github持续集成 提交代码到Github 从Github更新代码 git上显示构建状态 自动触发构建 Gi ...
- Jenkins 对项目持续集成的配置之二 API接口自动化 Ant+Jmeter
先介绍一下Ant+Jmeter 略 我的另一篇文章有讲在linux上部署ant + jmeter以满足CI持续化集成 https://www.cnblogs.com/qianjinyan/p/9067 ...
- Jenkins + Ant + Jmeter 对项目的接口进行CI持续集成的配置 外加发送邮件 sendEmail
Step1:安装Jenkins,从指定git上拉代码[安装步骤忽略] Step2:在项目安装的linux server上安装Ant 和Jmeter,我都安装在了自己的目录上,如下图 Step3:编写b ...
- [Jenkins][centos]1 持续集成 之 配置VNC,部署Jenkins
痛点:上一篇的AWS部署的VNC不知为啥挂了,死活连不上,因此改申请京东云做部署Jenkins 预计阅读时间:20分钟 更新软件,安装桌面 yum -y update yum -y groupinst ...
- [转] 基于Gitlab CI搭建持续集成环境
[From] https://blog.csdn.net/wGL3k77y9fR1k61T1aS/article/details/78798577 前言 本文是在12月12号迅雷@赵兵在前端早读课第三 ...
- 使用Jenkins+Calabash+Cocoapods搭建iOS持续集成环境
使用jenkins+calabash+cocoapods搭建ios持续集成环境 持续集成 持续集成到底是什么呢?依据敏捷大师Martin Fowler的定义: 持续集成是一种软件开发实践. 在持续集成 ...
随机推荐
- C++视频教学
http://open.163.com/movie/2010/1/E/4/M6LDTAPTU_M6LFSTGE4.html http://open.163.com/movie/2010/1/N/5/M ...
- 解决打包遇到的_mssql问题
明明上一篇还说着打包好了,这一个又出现了问题,真是让人揪心呀!错误如下: Traceback (most recent call last): File "macc.py", li ...
- axios post提交数据格式不对的问题
需要格式化一下 this.$http({ method: "post", url: "/chinacountry/index.php/home/Search/index& ...
- hadoop 使用Avro排序
在上例中,使用Avro框架求出数据的最大值,本例使用Avro对数据排序,输入依然是之前的样本,输出使用文本(也可以输出Avro格式). 1.在Avro的Schema中直接设置排序方向. dataRec ...
- [洛谷P4781]【模板】拉格朗日插值
题目大意:给你$n(n\leqslant2000)$个点,要你求$n-1$次经过这$n$个点的多项式在$k$处的值 题解:$Lagrange$插值:$$f_x=\sum\limits_{i=1}^ky ...
- [洛谷P3550][POI2013]TAK-Taxis
题目大意:一条路上有三个点,$0$为起始位置,$d$为总部,$m$为家.有$n$辆车,每辆车最多行驶$x_i$,都从$d$出发,可以在任意位置结束,问最少几辆车可以到家. 题解:贪心,发现当人在$[0 ...
- 2018牛客多校第六场 G.Pikachu
题意: 给出一棵n个点的树,每条边有边权.对这个树加边变成一个完全图.新加的边的权值为边上两点在树上的距离.求完全图上任意两点的最大流之和. 题解: 一共有C(n,2)个点对.假设当前求s到t之间的最 ...
- Android <Android应用开发实战> 资源类型<一>
1.字符串资源>>1.普通字符串>>2.字符串数组 <resources> <string-array name="planets_array&qu ...
- BZOJ4311:向量——题解
https://www.lydsy.com/JudgeOnline/problem.php?id=4311 你要维护一个向量集合,支持以下操作: 1.插入一个向量(x,y) 2.删除插入的第i个向量 ...
- BZOJ2597 [Wc2007]剪刀石头布 【费用流】
题目链接 BZOJ2597 题解 orz思维差 既然是一张竞赛图,我们选出任意三个点都可能成环 总方案数为 \[{n \choose 3}\] 如果三个点不成环,会发现它们的度数是确定的,入度分别为\ ...
