类扩展欧几里得 zquoj 26659

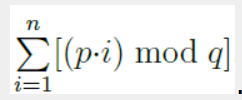
求该式子，因为只有里面mod  外面没mod；

所以先是把前面的等差数列求和，然后再减去模掉的部分；

这是类欧几里得模板题

 #include<bits/stdc++.h>
 #define pd putchar(' ')
 #define pn putchar('\n')
 #define pb push_back
 #define fi first
 #define se second
 #define f1(i,j,n) for(int i=j;i<n;i++)
 #define f2(i,j,n) for(int i=j;i<=n;i++)
 #define mem(i,j) memset(i,j,sizeof(i))
 #define INF 0x3f3f3f3f
 #define PI acos(-1.0)
 #define ll long long
 #define jiasu ios::sync_with_stdio(false)
 #define P1 printf("YES\n")
 #define P2 printf("NO\n")
 const ll mod = 1e9 +  ;
 const ll maxn = 1e5 +  ;
 const double eps = 1e- ;
 using namespace std;
 ll solve(ll a,ll b,ll c,ll n){

     //a 公差 b 首项 c 除数 n 项数
     if(n==) return b/c;
     if(n<=) return ;
     ll ans=(a/c)*((n-)*n/);
     ans+=(b/c)*n;
     a%=c;b%=c;
     if(a==)return ans;
     return ans+solve(c,(a*n+b)%c,a,(a*n+b)/c);
 }
 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--){
         ll p,q,n;
         scanf("%lld%lld%lld",&p,&q,&n);
         ll sum=p*n*(n+)/;
         ll res=solve(p,p,q,n)*q;
         printf("%lld\n",sum-res);
     }
     return ;
 }