svn使用方法以及使用教程
一、什么是svn
SVN是Subversion的简称,是一个开放源代码的版本控制系统,相较于RCS、CVS,它采用了分支管理系统,它的设计目标就是取代CVS。
二、svn的下载安装
下载地址:https://tortoisesvn.net/downloads.zh.html
安装完不要忘记重启电脑
安装完成后,按下鼠标右键,会看到如下界面: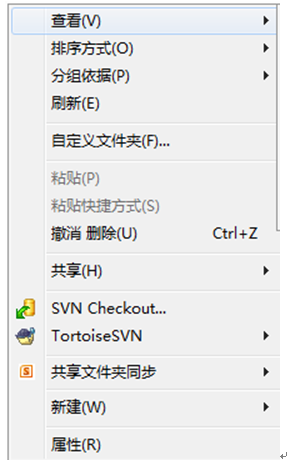
如果显示是这样的,就说明安装成功了
三、svn的常用操作
1、迁出配置库内容(SVN Checkout)
1.新建或进入目录下(比如E盘),右键 →SVN Checkout
2.URL of repository 填写仓库路径即可
3.Revision处,“HEAD revision”是指最新版,也可以指定Revision为任意一个版本。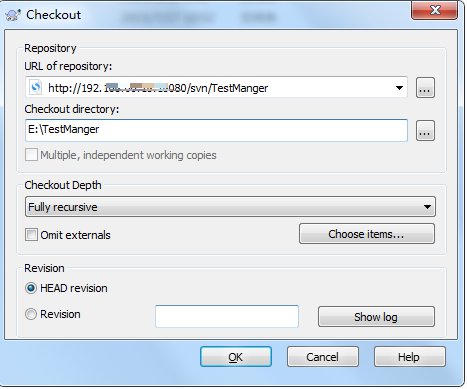
4.点击“OK”按钮后,在弹出的对话框中输入用户名和密码,验证成功后,项目文件开始从远程服务器下载到本地工作目录中:
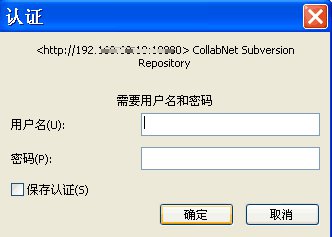
5.点击“确定”按钮后,即可获取完成,出现如下下载界面:
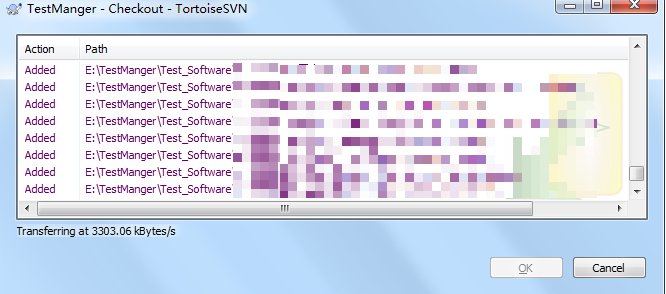
6.下载完成后,服务器上所有内容会出现在本地文件夹下
2、更新文件(SVN Update)
1.当从配置库迁出相应目录后,他人对服务器上此目录内容进行了修改,则需要再次获取改动内容到本地目录的过程称为更新。更新可以针对一个文件、几个选中的文件或者整个文件目录。
选中要被更新的文件,右键选择“SVN Update”项,如下: 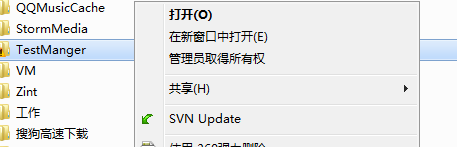
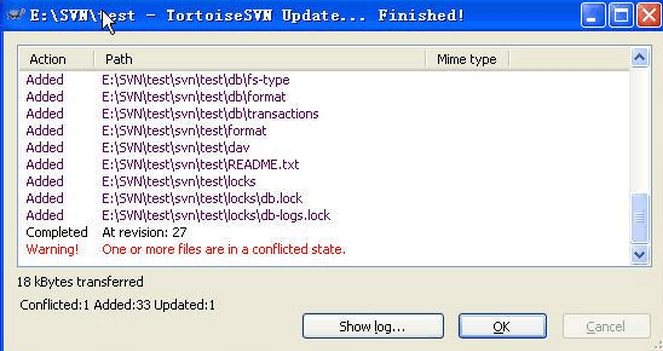
2)点击“SVN Update”后会弹出窗口显示更新的进度,如下:
若上述框中的有文件出现亮红,说明来自配置库的内容与你本地修改内容合并时出现了冲突
3、提交更新(SVN Commit)
本地文件修改后,若是需要更新到服务器上,则需要提交(Commit)最新的更新。
Commit的作用是将本地最新修改的文件同步到SVN服务端,供其他人来参考或者使用,当然使用之前,要先Update一下,来确保是最新的,在修改文件上击右键,出现菜单,选择“SVN Commit…”,如下: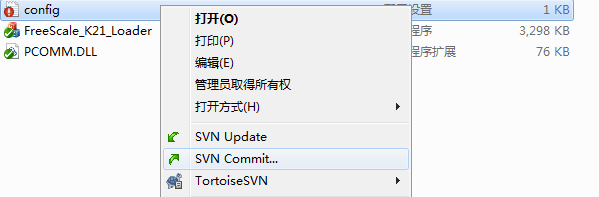
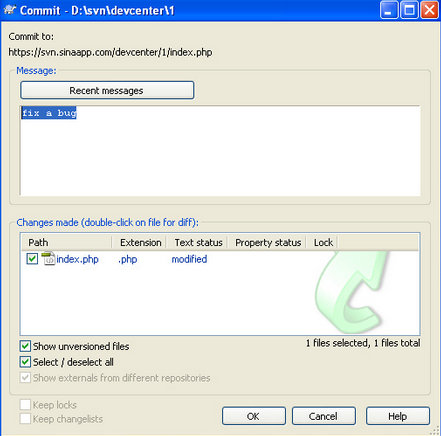
2.然后填写关于本次更新的日志(log message),这是必填项,否则commit会失败,如下:
4、增加文件(Add)
将需要增加的新文件放入到本地迁出的文件夹TestManger目录的相应位置中,鼠标选中新文件右键选择“Tortoise SVN”的“Add”项,如下图所示
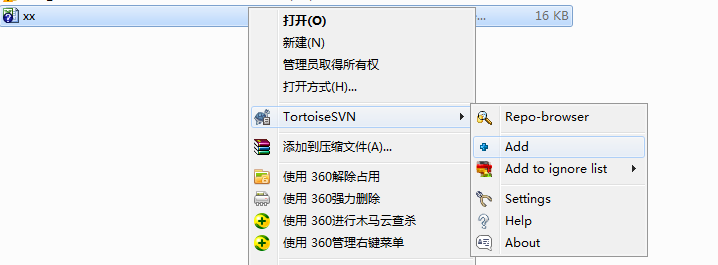
鼠标选中TestManger文件夹右键选择“SVN Commit…”,将新文件上传配置库对应文件夹中(若只上传单个文件,只需点中单个文件上传即可)。
5、检查更新(Check for modifications)
此功能可以显示本地对文件所做的修改有哪些还没有提交。不光能看到对文件的修改变化,还包括增加文件或目录,删除文件或目录,移动文件或目录等。当他人提交了哪些文件的改动,也可通过此项来进行查询。
6、删除文件(Delete)
选中要被删除的文件,右键选择“Tortoise SVN”的“Delete”项,如下: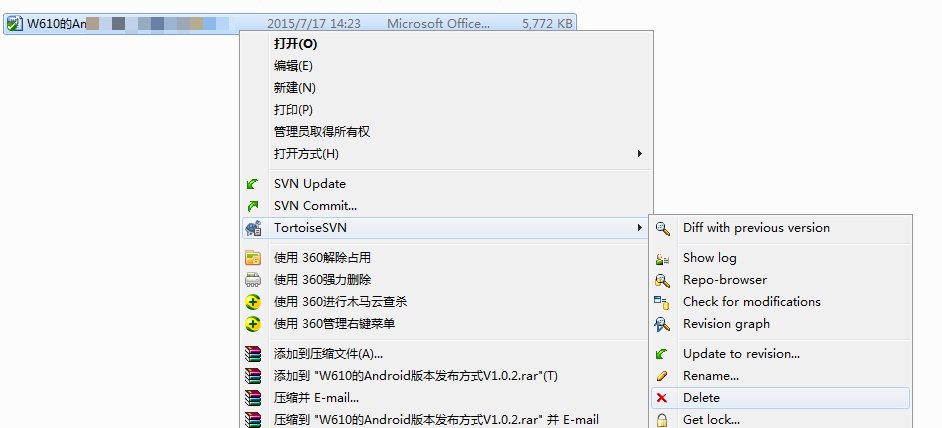
删除文件后,鼠标选中TestManger文件夹右键选择“SVN Commit…”项进行提交,提交方式同增加文件的提交方式,提交后则将新文件从配置库中删除。
7、撤销更改(Revert)
在修改了某些文件后(文件未上传到配置库),需要返回到修改前的状态,则选中文件夹右键选择“Tortoise SVN”的“Revert…”项进行撤销,本地硬盘上的文件将恢复到修改前的内容,修改的内容将被删除。
8、锁定和解锁(Get lock and Release lock)
当项目需要时可以在本地硬盘中将迁出的内容进行锁定,选中要被锁定的文件右键选择“Tortoise SVN”的“Get lock…”项进行锁定(锁定后他人将无法修改此文件),系统弹出锁定信息框。 当文本文件锁定后,需要通过解锁他人才能继续对文件进行修改。选中被锁定的文件右键选择“Tortoise SVN”的“Release lock…”项进行解锁。
9、重命名文件(Rename)
修改文件名,选中需要重命名的文件或文件夹,然后右键“Tortoise SVN”的“Rename”,在弹出的对话框中输入新名称,点击“OK”按钮,并将修改文件名后的文件或文件夹“SVN Commit…”提交到SVN服务器上。
10、获取历史文件(Show log)
Show log顾名思义是显示日志的作用,主要是显示该文件或者该目录被执行的操作,是被谁修改了,以及修改的时间和日期。鼠标选中文件夹右键选择“Tortoise SVN”的“Show log”项,系统弹出此路径下的所有文件版本信息,如下: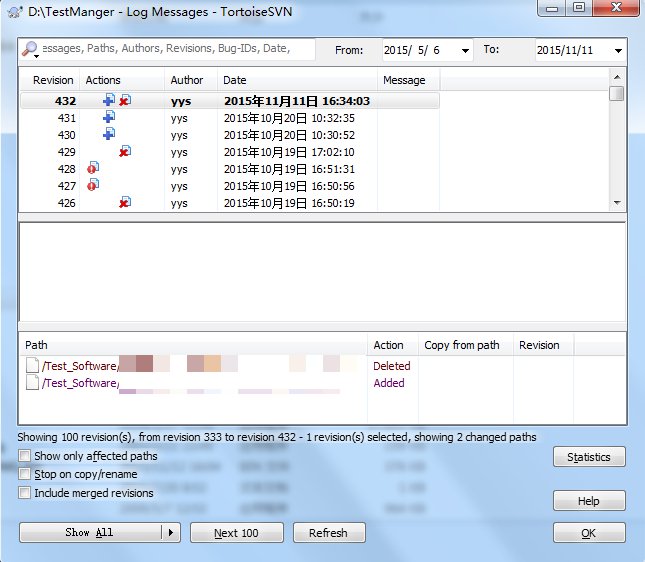
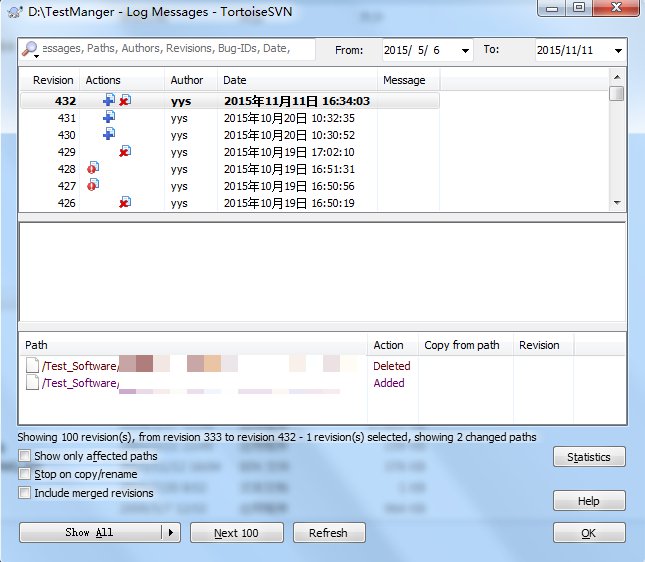
svn使用方法以及使用教程的更多相关文章
- SVN使用方法总结
SVN使用方法 SVN版本管理模式:http://www.cnblogs.com/newstar/archive/2011/01/04/svn.html (集中式-trunk和分散式-branch ...
- win8.1系统的安装方法详细图解教程
win8.1系统的安装方法详细图解教程 关于win8.1系统的安装其实很简单 但是有的童鞋还不回 所以今天就抽空做了个详细的图解教程, 安装win8.1系统最好用U盘安装,这样最方便简单 而且系统安装 ...
- C#读写文件的方法汇总_C#教程_脚本之家
C#读写文件的方法汇总_C#教程_脚本之家 http://www.jb51.net/article/34936.htm
- 360wifi使用方法|360wifi使用教程
360随身WiFi是一款超迷你.操作极其简单的无线路由器,只需把360随身WiFi插到一台可以上网的电脑上,不用做任何设置,就把连接有线网络的电脑转变成接入点,实现与其他终端的网络共享.简单方便实现手 ...
- MyEclipse SVN安装方法
方法一:在线安装 1.打开HELP->MyEclipse Configuration Center.切换到SoftWare标签页. 2.点击Add Site 打开对话框,在对话框Name输入Sv ...
- 【转】 Android Studio SVN 使用方法
Android Studio SVN 使用方法 如何安装配置SVN 请直接参考<SVN在Android Studio中的配置> http://www.cnblogs.com/songmen ...
- [转载]Tortoise SVN使用方法,简易图解
刚到公司实习,为了版本控制,我公司使用SVN控制版本,在此记下SVN使用方法,仅供参考! 废话少说,上图! ---------------------------------- ...
- PHP cURL实现模拟登录与采集使用方法详解教程
来源:http://www.zjmainstay.cn/php-curl 本文将通过案例,整合浏览器工具与PHP程序,教你如何让数据 唾手可得 . 对于做过数据采集的人来说,cURL一定不会陌生.虽然 ...
- myeclipse安装SVN插件方法
http://www.cnblogs.com/xdp-gacl/p/3497016.html myeclipse安装SVN插件方法 SVM China 源代码托管中心 http://www.svnch ...
随机推荐
- ECMAScript1.1 js书写位置 | 声明变量 | 基本数据类型 | 数据类型转换 | 操作符 | 布尔类型的隐式转换
js书写位置 由于在写css样式时使用的时双引号,所以我们在写js代码时建议使用单引号(‘’)! 行内式 <input type="button" value="点 ...
- 利用Python,方便局域网内上传下载文件
因为一直在用windows系统,最近需要用到linux的服务器,两个电脑之间总是需要来回拷贝文件 这样使得很繁琐,之前一直在用Python,开启一个简单的服务器,可以在另外一台同一局域网下的电脑,在线 ...
- 在Logstash的配置文件中对日志事件进行区分
1.多个日志文件作为输入源 input { # 通过给日志事件定义类型来区分 file { path => ["/var/log/nginx/access.log"] typ ...
- 错误Exception in thread "main" java.lang.NoClassDefFoundError: org/apache/hadoop/fs/FSDataInputStream排查思路
spark1(默认CDH自带版本)不存在这个问题,主要是升级了spark2(CDHparcel升级)版本安装后需要依赖到spark1的旧配置去读取hadoop集群的依赖包. 1./etc/spark2 ...
- 判断APP是否已安装
NSString *str = [NSString stringWithFormat:@"%@://%@",[dic objectForKey:@"ios_url_sch ...
- 【转】Windows(server2008)下使用VisualSVN Server搭建SVN服务器
参考文献 1.Windows下使用VisualSVN Server搭建SVN服务器(百度经验) 挺好就是没有配图已验证可用 2.在Windows Server 2008上部署SVN代码管理器 把第二 ...
- sql (5) 左右连接
左连接 SQL LEFT JOIN LEFT JOIN 关键字会从左表 (table_name1) 那里返回所有的行,即使在右表 (table_name2) 中没有匹配的行.语法SELECT colu ...
- Idea中创建maven骨架的命令
如下:通过命令化在Idea中创建骨架成功后,以后项目直接引用导入骨架直接在依赖框架上面进行相关模块开发: 1.mvn archetype:create-from-project 2.mvn clean ...
- 剑指Offer-13:调整数组位置使奇数位于偶数前面
题目描述: 输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变.例如给定一个数组 ...
- springboot2.x jpa接入多数据源
环境:springboot 2.1.4 数据源引入方式 数据源一 @Configuration @EnableTransactionManagement @EnableJpaRepositories( ...
