UVA 1347"Tour"（经典DP）

传送门

参考资料：

　　[1]:紫书

题意：

　　

　　欧几里得距离？？？？

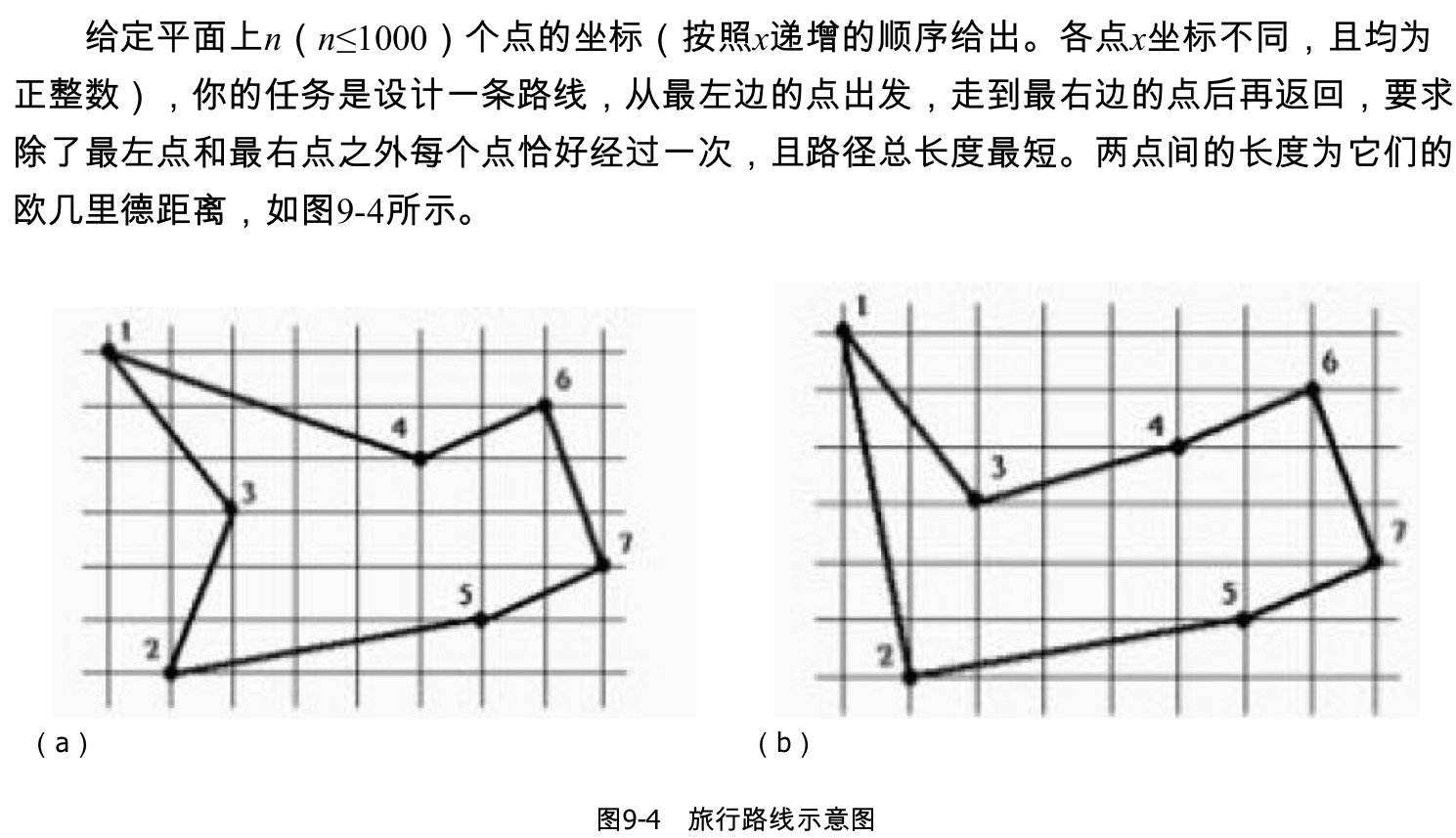
题解：

　　

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn=1e3+;

 int n;
 struct Point
 {
     int x,y;
     bool operator < (const Point& obj) const
     {
         return x < obj.x;
     }
 }p[maxn];
 ///dp[i][j]:前i个点全部走过，并且一个人在i点，一个人在j点
 ///从(i,j)状态到n点所需的最短距离
 double dp[maxn][maxn];

 double d(int a,int b)
 {
     return sqrt((p[a].x-p[b].x)*(p[a].x-p[b].x)+(p[a].y-p[b].y)*(p[a].y-p[b].y));
 }

 double Solve()
 {
     for(int i=;i < n-;++i)///预处理处dp[n-1][1,...,n-2]
         dp[n-][i]=d(n-,n)+d(i,n);
     for(int i=n-;i >= ;--i)
         for(int j=i-;j >= ;--j)
             dp[i][j]=min(dp[i+][j]+d(i,i+),dp[i+][i]+d(j,i+));

     return d(,)+dp[][];
 }
 int main()
 {
     while(~scanf("%d",&n))
     {
         for(int i=;i <= n;++i)
             scanf("%d%d",&p[i].x,&p[i].y);
         sort(p+,p+n+);
         printf("%.2f\n",Solve());
     }
     return ;
 }