【动手学pytorch】softmax回归

一、什么是softmax？

有一个数组S，其元素为S_i ，那么v_i 的softmax值，就是该元素的指数与所有元素指数和的比值。具体公式表示为：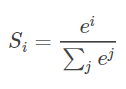

softmax回归本质上也是一种对数据的估计

二、交叉熵损失函数

在估计损失时，尤其是概率上的损失，交叉熵损失函数更加常用。下面是交叉熵

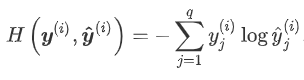
当我们预测单个物体（即每个样本只有1个标签），y⁽ⁱ⁾为我们构造的向量，其分量不是0就是1，并且只有一个1（第y⁽ⁱ⁾个数为1）。于是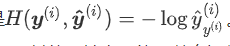。交叉熵只关心对正确类别的预测概率，因为只要其值足够大，就可以确保分类结果正确。遇到一个样本有多个标签时，例如图像里含有不止一个物体时，我们并不能做这一步简化。但即便对于这种情况，交叉熵同样只关心对图像中出现的物体类别的预测概率。

交叉熵函数为：

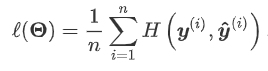
三、获取Fashion-MNIST训练集和读取数据

我这里我们会使用torchvision包，它是服务于PyTorch深度学习框架的，主要用来构建计算机视觉模型。torchvision主要由以下几部分构成：

torchvision.datasets: 一些加载数据的函数及常用的数据集接口；
torchvision.models: 包含常用的模型结构（含预训练模型），例如AlexNet、VGG、ResNet等；
torchvision.transforms: 常用的图片变换，例如裁剪、旋转等；
torchvision.utils: 其他的一些有用的方法。
```
from IPython import display

import matplotlib.pyplot as plt

import torch

import torchvision

import torchvision.transforms as transforms

import time

import sys

sys.path.append("/home/kesci/input")

import d2lzh1981 as d2l

#get datatest。如果不设置train的值，那么就同时返回train和test，此时的操作见“四”中的第二个代码块

mnist_train = torchvision.datasets.FashionMNIST(root='/home/kesci/input/FashionMNIST2065', train=True, download=True, transform=transforms.ToTensor())

mnist_test = torchvision.datasets.FashionMNIST(root='/home/kesci/input/FashionMNIST2065', train=False, download=True, transform=transforms.ToTensor())
```
class torchvision.datasets.FashionMNIST(root, train=True, transform=None, target_transform=None, download=False)
- root（string）– 数据集的根目录，其中存放processed/training.pt和processed/test.pt文件。
- train（bool, 可选）– 如果设置为True，从training.pt创建数据集，否则从test.pt创建。
- download（bool, 可选）– 如果设置为True，从互联网下载数据并放到root文件夹下。如果root目录下已经存在数据，不会再次下载。
- transform（可被调用 , 可选）– 一种函数或变换，输入PIL图片，返回变换之后的数据。如：transforms.RandomCrop。
- target_transform（可被调用 , 可选）– 一种函数或变换，输入目标，进行变换。

# show result

print(type(mnist_train))

print(len(mnist_train), len(mnist_test))

<class 'torchvision.datasets.mnist.FashionMNIST'>

60000 10000

# 我们可以通过下标来访问任意一个样本

feature, label = mnist_train[0]

print(feature.shape, label)  # Channel x Height x Width

torch.Size([1, 28, 28]) 9

#如果不做变换输入的数据是图像，我们可以看一下图片的类型参数

mnist_PIL = torchvision.datasets.FashionMNIST(root='/home/kesci/input/FashionMNIST2065', train=True, download=True)

PIL_feature, label = mnist_PIL[0]

print(PIL_feature)

<PIL.Image.Image image mode=L size=28x28 at 0x7F54A41612E8>

# 本函数已保存在d2lzh包中方便以后使用

def get_fashion_mnist_labels(labels):

    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',

                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']

    return [text_labels[int(i)] for i in labels]

def show_fashion_mnist(images, labels):

    d2l.use_svg_display()

    # 这里的_表示我们忽略（不使用）的变量

    _, figs = plt.subplots(1, len(images), figsize=(12, 12))

    for f, img, lbl in zip(figs, images, labels):

        f.imshow(img.view((28, 28)).numpy())

        f.set_title(lbl)

        f.axes.get_xaxis().set_visible(False)

        f.axes.get_yaxis().set_visible(False)

    plt.show()

X, y = [], []

for i in range(10):

    X.append(mnist_train[i][0]) # 将第i个feature加到X中

    y.append(mnist_train[i][1]) # 将第i个label加到y中

show_fashion_mnist(X, get_fashion_mnist_labels(y))

# 读取数据

batch_size = 256

num_workers = 4

train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)

test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)

start = time.time()

for X, y in train_iter:

    continue

print('%.2f sec' % (time.time() - start))

四、从零开始的softmax

import torch

import torchvision

import numpy as np

import sys

sys.path.append("/home/kesci/input")

import d2lzh1981 as d2l

 #获取训练集数据和测试集数据

 batch_size = 256

 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, root='/home/kesci/input/FashionMNIST2065')

 #模型参数初始化

 num_inputs = 784

 print(28*28)

 num_outputs = 10

 W = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_outputs)), dtype=torch.float)

 b = torch.zeros(num_outputs, dtype=torch.float)

 784

 W.requires_grad_(requires_grad=True)

 b.requires_grad_(requires_grad=True)

#对多维数组的操作

X = torch.tensor([[1, 2, 3], [4, 5, 6]])

print(X.sum(dim=0, keepdim=True))  # dim为0，按照相同的列求和，并在结果中保留列特征

print(X.sum(dim=1, keepdim=True))  # dim为1，按照相同的行求和，并在结果中保留行特征

print(X.sum(dim=0, keepdim=False)) # dim为0，按照相同的列求和，不在结果中保留列特征

print(X.sum(dim=1, keepdim=False)) # dim为1，按照相同的行求和，不在结果中保留行特征

tensor([[5, 7, 9]])

tensor([[ 6],

        [15]])

tensor([5, 7, 9])

tensor([ 6, 15])

定义softmax：

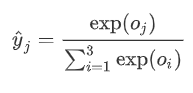
 def softmax(X):

     X_exp = X.exp()                                            #对所有分量求exp

     partition = X_exp.sum(dim=1, keepdim=True)

     print("X size is ", X_exp)

     print("partition size is ", partition, partition.size())

     return X_exp / partition                

 X = torch.rand((2, 5))

 X_prob = softmax(X)

 print(X_prob, '\n', X_prob.sum(dim=1))

 #如果我们不在sum那一步设置 keepdim=True，那么partition会变成一个1×2而不是2×1的矩阵

 X size is  tensor([[2.1143, 1.4179, 2.1258, 2.3031, 1.2574],

         [1.1700, 1.1645, 1.1296, 1.8801, 1.3726]])

 partition size is  tensor([[9.2185],

         [6.7168]]) torch.Size([2, 1])

 tensor([[0.2253, 0.1823, 0.1943, 0.2275, 0.1706],

         [0.1588, 0.2409, 0.2310, 0.1670, 0.2024]])

 tensor([1.0000, 1.0000])    #说明所有样本出现的概率之和为1

建立回归模型

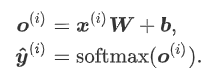
def net(X):

    #行维度未知，列维度为输入值。此时写为.view(-1,num_inputs)。即行列哪一个未知，哪一个就写-1。
    #如果是torch.view(-1)，则原张量会变成一维的结构。即把所有分量全部整合到一个向量中

    return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)

定义损失函数

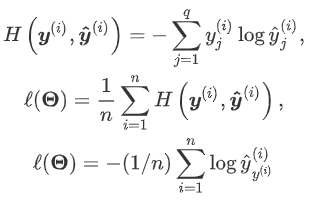
def cross_entropy(y_hat, y):

    return - torch.log(y_hat.gather(1, y.view(-1, 1)))#取对应第y(i)个的y_hat

补充：gather(input, dim, index)或input.gather(dim,index)

index由tensor类型提供。dim主要决定以行（0）还是以列（1）进行运算

下面的例子中因为按照列，并且

y.view(-1, 1)=(0,2)',为列向量
所以下面代码的意思是，按照列来看，取第一行的第0列分量（0.1）和第二行的第2列分量（0.5）

y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])

y = torch.LongTensor([0, 2])

y_hat.gather(1, y.view(-1, 1))

tensor([[0.1000],

        [0.5000]])

定义准确率

完成预测后需要准确率函数进行检验

def accuracy(y_hat, y):

    return (y_hat.argmax(dim=1) == y).float().mean().item()　　#.argmax(dim=1)按照行取最大值。
#如果与真实值相同就为1，否则为0.然后计算他们的平均值

print(accuracy(y_hat, y))

# 求平均准确率。本函数已保存在d2lzh_pytorch包中方便以后使用。该函数将被逐步改进：它的完整实现将在“图像增广”一节中描述

def evaluate_accuracy(data_iter, net):

    acc_sum, n = 0.0, 0

    for X, y in data_iter:

        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()

        n += y.shape[0]

    return acc_sum / n

print(evaluate_accuracy(test_iter, net))

训练模型

num_epochs, lr = 5, 0.1

# 本函数已保存在d2lzh_pytorch包中方便以后使用

def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,

              params=None, lr=None, optimizer=None):

    for epoch in range(num_epochs):

        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
　　　　　#train_l为训练损失，train_acc为训练准确率

        for X, y in train_iter:

            y_hat = net(X)

            l = loss(y_hat, y).sum()

            # 梯度清零

            if optimizer is not None:

                optimizer.zero_grad()

            elif params is not None and params[0].grad is not None:

                for param in params:

                    param.grad.data.zero_()

            l.backward()

            if optimizer is None:

                d2l.sgd(params, lr, batch_size)

            else:

                optimizer.step() 

            train_l_sum += l.item()

            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()

            n += y.shape[0]

        test_acc = evaluate_accuracy(test_iter, net)

        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'

              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)

模型预测

现在我们的模型训练完了，可以进行一下预测，我们的这个模型训练的到底准确不准确。现在就可以演示如何对图像进行分类了。给定一系列图像（第三行图像输出），我们比较一下它们的真实标签（第一行文本输出）和模型预测结果（第二行文本输出）。

X, y = iter(test_iter).next()

true_labels = d2l.get_fashion_mnist_labels(y.numpy())#真实标签

pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())#预测标签

titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]

d2l.show_fashion_mnist(X[0:9], titles[0:9])

五、pytorch的简单实现

import torch

from torch import nn

from torch.nn import init

import numpy as np

import sys

sys.path.append("/home/kesci/input")

import d2lzh1981 as d2l

#初始化参数和获取数据

batch_size = 256

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, root='/home/kesci/input/FashionMNIST2065')

#定义网络模型（即回归模型）

num_inputs = 784    #28×28

num_outputs = 10    #10种类型的图片

class LinearNet(nn.Module):

    def __init__(self, num_inputs, num_outputs):

        super(LinearNet, self).__init__()

        self.linear = nn.Linear(num_inputs, num_outputs)

    def forward(self, x): # x 的形状: (batch, 1, 28, 28)

        y = self.linear(x.view(x.shape[0], -1))

        return y

# net = LinearNet(num_inputs, num_outputs)

class FlattenLayer(nn.Module):

    def __init__(self):

        super(FlattenLayer, self).__init__()

    def forward(self, x): # x 的形状: (batch, *, *, ...)

        return x.view(x.shape[0], -1)

from collections import OrderedDict

net = nn.Sequential(

        # FlattenLayer(),

        # LinearNet(num_inputs, num_outputs)

        OrderedDict([

           ('flatten', FlattenLayer()),

           ('linear', nn.Linear(num_inputs, num_outputs))]) # 或者写成我们自己定义的 LinearNet(num_inputs, num_outputs) 也可以

        )

 #初始化模型参数

init.normal_(net.linear.weight, mean=0, std=0.01)

init.constant_(net.linear.bias, val=0)

#定义损失函数

loss = nn.CrossEntropyLoss() # 下面是他的函数原型

# class torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

#定义优化函数

optimizer = torch.optim.SGD(net.parameters(), lr=0.1) # 下面是函数原型

# class torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)

#训练

num_epochs = 5

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)