2017CCPC杭州(ABCDJ)

所有的题目在这里<---

待补...

Problem A. HDU6264:Super-palindrome

题意：

　　题目定义了一个超级回文串，这个串满足：它的任一奇数长度的串都是回文串。

　　现在给你一个字符串，问你把它变成超级回文串需要多少次操作。每次操作可以把一个字符变成其他任一字符。

题解：

　　显然，一个串只有符合　整个串奇数位字符都相同，偶数位字符都相同，奇数位偶数位字符不一定要相同(包含了字符全相同的情况)时满足超级回文。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = ;
int main(){
    int T;
    scanf("%d",&T);
    for (int t = ; t <= T; ++t) {
        string s;
        cin >> s;
        int a1[]={},a2[]={};
        int l = s.length(),num1=,num2=;
        for (int i = ; i < l; ++i) {
            if (i%) num2 = max(num2,++a2[s[i]]);
            else num1 = max(num1,++a1[s[i]]);
        }
        printf("%d\n",(l/-num1)+(l-l/-num2));
    }
    return ;
}

Problem B.HDU6265:Master of Phi

题意：

　　求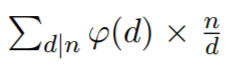 

题解：

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = ;
ll qp(ll a, ll b){
    ll ans = ;
    while (b) {
        if (b&) ans = (ans * a) % mod;
        a = (a * a) % mod;
        b >>= ;
    }
    return ans;
}
int main() {
    int T,n;
    scanf("%d",&T);
    while (T--) {
        ll ans = ,p,q;
        scanf("%d",&n);
        for (int i = ; i < n; i++){
            scanf("%lld%lld",&p,&q);
            ans=(ans*(qp(p,q)+((p-)*q%mod)*qp(p,q-)%mod))%mod;
        }
        printf("%lld\n",ans);
    }
    return ;
}

 

Problem C.HDU6266:Hakase and Nano

题意：

　　有n堆石子，每次可以选择任意一堆从中取至少一个石子，谁最后取完谁赢。

　　Hakase取两次，Nano取一次，两个人轮流取。问 Hakase是否能赢。

题解：

　　一堆石子如果只有一个，那么一次就取走了一堆，堆数减少；否则这一堆可以有剩余，堆数可以不变。

　　当 Hakase先取石子时，只有在每堆石子数量都为1且堆数是3的倍数时 Hakase会输，其余情况都会赢。

　　当 Nano先取石子时，Nano拿了第一次之后，就相当于成了Hakase先手。所以要使Hakase输需要使Nano拿了第一次之后每堆石子数量都为1且剩下的堆数是三的倍数，否则Hakase赢。这时有3种情况：

　　1.每堆石子都为1，且　堆数-1　是3的倍数。

　　2.只有一堆石子数量不为1，Nano将这堆石子全拿走，剩下 n-1堆石子数量全为1，且 n-1 是3的倍数。

　　3.只有一堆石子数量不为1，Nano将这堆石子剩一个，剩下 n 堆石子数量全为1，且 n 是3的倍数。

　　只有以上4种情况输出No，否则都是Yes。判断一下就行了。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = ;
int main(){
    int T,n,d,x;
    scanf("%d",&T);
    while (T--){
        int num = ;
        scanf("%d%d",&n,&d);
        for (int i = ; i < n; ++i) {
            scanf("%d",&x);
            if (x == ) num++;
        }
        bool fg = ;
        if (n == num) {
            num %= ;
            if (d ==  && !num) fg = ;
            else if (d ==  && num == ) fg = ;
        } else if (n == num+) {
            if (d == &&((n%)==||(num%)==)) fg = ;
        }
        printf("%s\n",fg?"Yes":"No");
    }
    return ;
}

Problem D. HDU6267Master of Random

题意：

　　之前没看到样例二的解释，然后搞了很久才弄懂题目意思...

　　有一颗树节点由0~n-1编号，0为根节点，其余点i的父节点随机在(0,i-1)中选一个，问所有情况下所有子树的和除以子树个数后的答案。

　　答案可能很大需要mod 998244353。

题解：

　　看懂题意之后就很好做了。

　　我们可以先把由1~4个节点组成的符合条件的树先画出来：

　　

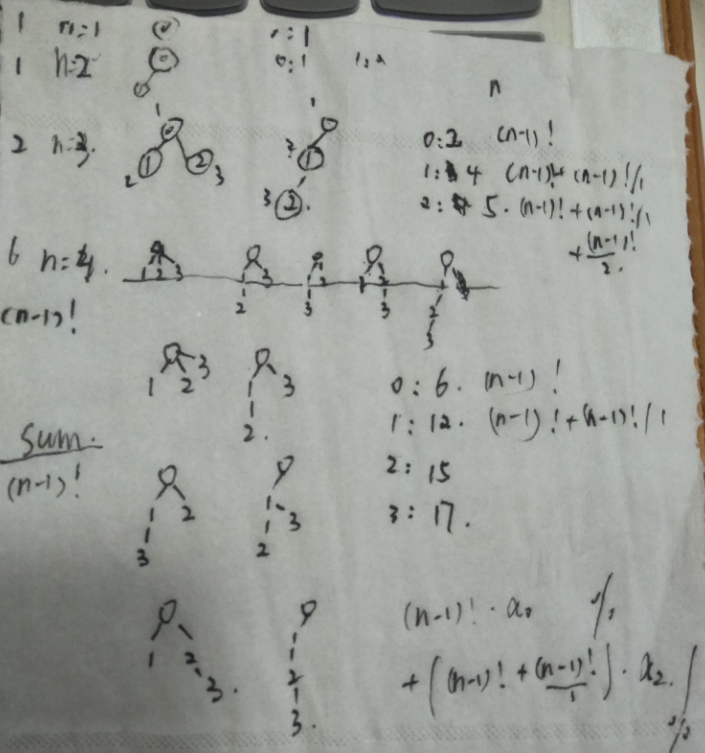
　　显然我们能发现，当节点数量为n时，节点0~n-1分别被计算了：

　　0 : (n-1)!
　　1 : (n-1)! + (n-1)!/1　
       2 : (n-1)! + (n-1)!/1 +(n-1)!/2
　　......
　　n-1 : (n-1)! + (n-1)!/1 +(n-1)!/2+...+(n-1)!/(n-1)

　　那么我们能得到所有的子树和和为(n-1)! * a[0] + ((n-1)! + (n-1)!/1) * a[1] + ... + ( (n-1)! + (n-1)!/1 +(n-1)!/2+...+(n-1)!/(n-1) ) * a[n-1]

　　子树个数为 (n-1)! * n  (树的排列方式数 * 节点数)
　　因为有除法取摸，所以要用到逆元　a^(mod-2)
 代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = ;
ll pq(ll a, ll b){
    ll ans = ;
    while (b) {
        if (b&) ans = (ans * a) % mod;
        a = (a * a) % mod;
        b >>= ;
    }
    return ans;
}
ll ive(ll x) {
    return pq(x,mod-);
}
int main() {
    int T,n;
    scanf("%d",&T);
    while (T--) {
        ll fm = , x;
        scanf("%d%lld",&n,&x);
        for (ll i = ; i < n; i++){
            fm = (fm*i)%mod;
        }
        ll num = fm, ans = (fm * x) % mod;
        for (int i = ; i < n; ++i) {
            scanf("%lld",&x);
            num = (num + fm*ive(i))%mod;
            ans = (ans + num*x%mod)%mod;
        }
        fm = (fm*n)%mod;
        printf("%lld\n",ans*ive(fm)%mod);
    }
    return ;
}

Problem J. HDU6273:Master of GCD

题意：

　　一开始有n个全为1的数，每次操作你选择一个区间[l,r]和一个x，将这个区间内的每个数更新为乘以x之后的值，x只能是2或者3。问m次操作之后，所有数的最大公约数是多少。

题解：

　　一开始所有数都为1，然后对每个区间的数进行乘法运算，那么所有数的最大公约数就是他们乘的同一个数的最小次方的乘积。

　　例如：假设3个1，第一个乘了2次2和3次3，第二一个乘了3次2和2次3，第三个乘了4次2和1次3。那么他们的最大公约数为2的2次方与3的1次方的乘积。

　　那么我们只需要记录一下每个数乘了几次2和3就行了。一开始用的树状数组，后来发现可以直接用前缀和。算结果时用快速幂取模即可。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+;
const int INF = 1e9+;
const ll mod = ;
ll num2[N],num3[N];
int T,n,m;
int lowbit(int x){
    return x&(-x);
}
void update(int id,ll *a, ll x) {
    while (id <= n) {
        a[id] +=x;
        id += lowbit(id);
    }
}

ll query(int id, ll *a) {
    ll r = ;
    while (id > ) {
        r += a[id];
        id -= lowbit(id);
    }
    return r;
}
ll pq(ll a, ll b) {
    ll r = ;
    while (b) {
        if (b&) r = (r*a) % mod;
        a = (a*a) % mod;
        b>>=;
    }
    return r;
}
int main()
{
    scanf("%d",&T);
    while(T--) {
        scanf("%d%d",&n,&m);
        memset(num2,,sizeof(num2));
        memset(num3,, sizeof(num3));
        for (int i = ; i < m; ++i) {
            int l,r,x;
            scanf("%d%d%d",&l,&r,&x);
            if (x == ){
                update(l,num2,);
                update(r+,num2,-);
            }else {
                update(l,num3,);
                update(r+,num3,-);
            }
        }
        ll n2 = query(,num2),n3 = query(,num3);
        for (int i = ; i <= n; i++) {
            n2 = min(n2,query(i,num2));
            n3 = min(n3,query(i,num3));
        }
        printf("%lld\n",(pq(,n2)*pq(,n3))%mod);
    }
    return ;
}

树状数组

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = +;
const int INF = 1e9+;
const ll mod = ;
int a[][N];
ll pq(ll a, ll b){
    ll ans = ;
    while (b) {
        if (b&) ans = (ans * a) % mod;
        a = (a * a) % mod;
        b >>= ;
    }
    return ans;
}
int main() {
    int T,n,m;
    scanf("%d",&T);
    while (T--){
        scanf("%d%d",&n,&m);
        memset(a,,sizeof(a));
        for (int i = ; i < m; ++i) {
            int l,r,x;
            scanf("%d%d%d",&l,&r,&x);
            a[x-][l]++;
            a[x-][r+]--;
        }
        ll n2, n3, sum2 , sum3;
        n2 = sum2 = a[][];
        n3 = sum3 = a[][];
        for (int i = ; i <= n; ++i) {
            sum2 += a[][i];
            n2 = min(sum2,n2);
            sum3 += a[][i];
            n3 = min(sum3,n3);
        }
        printf("%lld\n",(pq(,n2) * pq(,n3))%mod);
    }
    return ;
}

前缀和