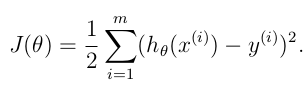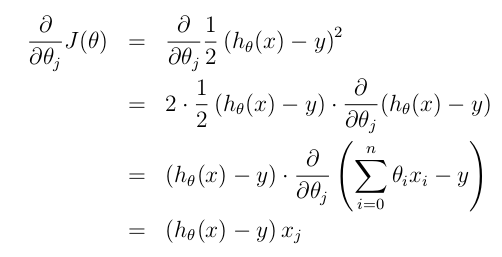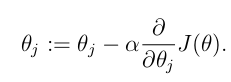BP 算法之一种直观的解释
0. 前言
之前上模式识别课程的时候,老师也讲过 MLP 的 BP 算法, 但是 ppt 过得太快,只有一个大概印象。后来课下自己也尝试看了一下 stanford
deep learning 的 wiki, 还是感觉似懂非懂,不能形成一个直观的思路。趁着这个机会,我再次 revisit 一下。本文旨在说明对 BP 算法的直观印象,以便迅速写出代码,具体偏理论的链式法则可以参考我的下一篇博客(都是图片,没有公式)。
1. LMS 算法
故事可以从线性 model 说起(顺带复习一下)~在线性 model 里面,常见的有感知机学习算法、 LMS 算法等。感知机算法的损失函数是误分类点到 Target 平面的总距离,直观解释如下:当一个实例点被误分,则调整 w, b 的值,使得分离超平面向该误分类点的一侧移动,以减少该误分类点与超平面的距离,在 Bishop 的 PRML一书中,有一个非常优雅的图展现了这个过程。但是了解了 MLP 的 BP 算法之后,感觉这个算法与
LMS 有点相通之处。虽然从名字上 MLP 叫做多层感知机,感知机算法是单层感知机。
LMS (Least mean squares) 算法介绍比较好的资料是 Andrew Ng cs229 的 Lecture Notes。假设我们的线性
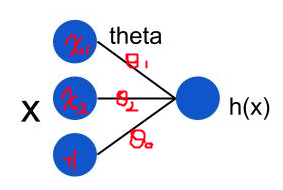
model 是这样的:
在上面这个模型中,用公式可以表达成:
如何判断模型的好坏呢?损失函数定义为输出值 h(x) 与目标值 y 之间的“二乘”:
对偏导进行求解,可以得到:
如果要利用 gradient descent 的方法找到一个好的模型,即一个合适的 theta 向量,迭代的公式为:
所以,对于一个第 i 个单独的训练样本来说,我们的第 j 个权重更新公式是:
这个更新的规则也叫做 Widrow-Hoff learning rule, 从上到下推导下来只有几步,没有什么高深的理论,但是,仔细观察上面的公式,就可以发现几个 natural and intuitive 的特性。
首先,权重的更新是跟 y - h(x) 相关的,如果训练样本中预测值与 y 非常接近,表示模型趋于完善,权重改变小。反之,如果预测值与 y 距离比较远,说明模型比较差,这时候权重变化就比较大了。
权重的变化还与 xi 也就是输入节点的值相关。也就是说,在同一次 train 中,由于 y - h(x) 相同, 细线上的变化与相应的输入节点 x 的大小是成正比的(参考最上面的模型图)。这中间体现的直观印象就是:残差的影响是按照 xi 分配到权重上去滴,这里的残差就是 h(x) - y。
LMS 算法暂时先讲到这里,后面的什么收敛特性、梯度下降之类的有兴趣可以看看 Lecture Notes。
2. MLP 与 BP 算法
前面我们讲过 logistic regression, logistic regression
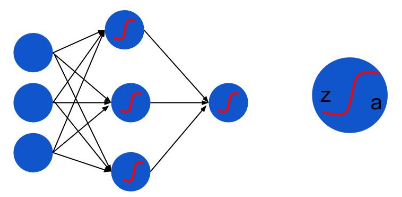
本质上是线性分类器,只不过是在线性变换后通过 sigmoid 函数作非线性变换。而神经网络 MLP 还要在这个基础上加上一个新的nonlinear function, 为了讨论方便,这里的 nonlinear function 都用 sigmoid 函数,并且损失函数忽略 regulization term, 那么, MLP 的结构就可以用下面这个图来表示:
z: 非线性变换之前的节点值,实际上是前一层节点的线性变换
a: 非线性变换之后的 activation 值a=f(z): 这里就是 sigmoid function
现在我们要利用 LMS 中的想法来对这个网络进行训练。
假设在某一个时刻,输入节点接受一个输入, MLP 将数据从左到右处理得到输出,这时候产生了残差。在第一小节中,我们知道, LMS 残差等于 h(x) - y。 MLP 的最后一层和 LMS 线性分类器非常相似,我们不妨先把最后一层的权重更新问题解决掉。在这里输出节点由于增加了一个非线性函数,残差的值比 LMS 的残差多了一个求导 (实际上是数学上 chain rule 的推导):

得到残差,根据之前猜想出来的规律( - -!), 残差的影响是按照左侧输入节点的 a 值大小按比例分配到权重上去的,所以呢,就可以得到:

如果乘以一个 learning rate, 这就是最后一层的权重更新值。
我们在想,要是能得到中间隐层节点上的残差,问题就分解成几个我们刚刚解决的问题。关键是:中间隐层的残差怎么算?
实际上就是按照权重与残差的乘积返回到上一层。完了之后还要乘以非线性函数的导数( again it can be explained by chain rule):

得到隐层的残差,我们又可以得到前一层权重的更新值了。这样问题就一步一步解决了。
最后我们发现,其实咱们不用逐层将求残差和权值更新交替进行,可以这样:
先从右到左把每个节点的残差求出来(数学上表现为反向传导过程)
然后再求权重的更新值
更新权重
Q: 这是在 Ng 教程中的计算过程, 但是在有些资料中,比如参考资料 [2],残差和权值更新是逐层交替进行的,那么,上一层的残差等于下一层的残差乘以更新后的权重,明显,Ng 的教程是乘以没有更新的权重,我觉得后者有更好的数学特性,期待解疑!
用一张粗略的静态图表示残差的反向传播:
红色的曲线就是对 sigmoid function 的求导,和高斯分布非常相似。
用一张动态图表示前向(FP)和后向(BP)传播的全过程:
OK,现在 BP 算法有了一个直观的思路,下面,将从反向传导的角度更加深入地分析一下 BP 算法。
BP 算法之一种直观的解释的更多相关文章
- BP算法从原理到python实现
BP算法从原理到实践 反向传播算法Backpropagation的python实现 觉得有用的话,欢迎一起讨论相互学习~Follow Me 博主接触深度学习已经一段时间,近期在与别人进行讨论时,发现自 ...
- 如何直观的解释back propagation算法?
转自:知乎-https://www.zhihu.com/question/27239198 作者:匿名用户链接:https://www.zhihu.com/question/27239198/answ ...
- (转)神经网络和深度学习简史(第一部分):从感知机到BP算法
深度|神经网络和深度学习简史(第一部分):从感知机到BP算法 2016-01-23 机器之心 来自Andrey Kurenkov 作者:Andrey Kurenkov 机器之心编译出品 参与:chen ...
- 从 0 开始机器学习 - 神经网络反向 BP 算法!
最近一个月项目好忙,终于挤出时间把这篇 BP 算法基本思想写完了,公式的推导放到下一篇讲吧. 一.神经网络的代价函数 神经网络可以看做是复杂逻辑回归的组合,因此与其类似,我们训练神经网络也要定义代价函 ...
- stanford coursera 机器学习编程作业 exercise4--使用BP算法训练神经网络以识别阿拉伯数字(0-9)
在这篇文章中,会实现一个BP(backpropagation)算法,并将之应用到手写的阿拉伯数字(0-9)的自动识别上. 训练数据集(training set)如下:一共有5000个训练实例(trai ...
- 如何高效的通过BP算法来训练CNN
< Neural Networks Tricks of the Trade.2nd>这本书是收录了1998-2012年在NN上面的一些技巧.原理.算法性文章,对于初学者或者是正在学习NN的 ...
- 人工神经网络反向传播算法(BP算法)证明推导
为了搞明白这个没少在网上搜,但是结果不尽人意,最后找到了一篇很好很详细的证明过程,摘抄整理为 latex 如下. (原文:https://blog.csdn.net/weixin_41718085/a ...
- 多层感知机及其BP算法(Multi-Layer Perception)
Deep Learning 近年来在各个领域都取得了 state-of-the-art 的效果,对于原始未加工且单独不可解释的特征尤为有效,传统的方法依赖手工选取特征,而 Neural Network ...
- 关于BP算法在DNN中本质问题的几点随笔 [原创 by 白明] 微信号matthew-bai
随着deep learning的火爆,神经网络(NN)被大家广泛研究使用.但是大部分RD对BP在NN中本质不甚清楚,对于为什这么使用以及国外大牛们是什么原因会想到用dropout/sigmoid ...
随机推荐
- Delphi exe实例之间传递cmd参数
{Unit1.pas} 通过这个单元的Button,调用另一个实例: procedure TForm1.Button1Click(Sender: TObject); begin ShellExecut ...
- Vue-cli中使用vConsole,以及设置JS连续点击控制vConsole按钮显隐功能实现
最近发现了一个鹅厂的仓库,实现起来比我这个方便[捂脸].https://github.com/AlloyTeam/AlloyLever 一.vue-cli脚手架中搭建的项目引入vConsole调试 1 ...
- 简单理解vue的slot插槽
slot的意思是插槽,想想你的电脑主板上的各种插槽,有插CPU的,有插显卡的,有插内存的,有插硬盘的,所以假设有个组件是computer,其模板是 <template> <div&g ...
- git 安装 使用过程遇到的问题
git add "文件名"->git commit -m 'add' ->>git push origin develop 1.git基础之切换分支 选择gi ...
- JAVA IntelliJ IDEA for mac/jdk的安装及环境配置、运行
现在配置完之后再回头看看,其实挺简单, 但我还是弄了好几个小时才配置出来, 不过好在是自己配置出来的, 每天都在慢慢进步. 安装及配置步骤如下: JAVA的IDE的话去jetbrains的官网上对应下 ...
- 2014 0416 word清楚项目黑点 输入矩阵 普通继承和虚继承 函数指针实现多态 强弱类型语言
1.word 如何清除项目黑点 选中文字区域,选择开始->样式->全部清除 2.公式编辑器输入矩阵 先输入方括号,接着选择格式->中间对齐,然后点下面红色框里的东西,组后输入数据 ...
- SparkStreaming整合Flume的pull方式之启动报错解决方案
Flume配置文件: simple-agent.sources = netcat-source simple-agent.sinks = spark-sink simple-agent.channel ...
- RobotFramework Selenium2 EXCUTE JAVASCRIPT
https://www.cnblogs.com/lixy-88428977/p/9563247.html
- Algo: Basic
1. 二维数组的查找 2. 替换空格 3. 从尾到头打印链表 4. 重建二叉树 5. 用两个栈实现队列 6. 旋转数组的最小数字 7. 斐波那契数列 8. 跳台阶 9. 变态跳台阶 10. 矩阵覆盖 ...
- 实现虚拟机VMware上Linux与本机windows互相复制与粘贴的问题
解决方法:只需要在Linux系统中安装一个vmware-tools的工具 1.选择虚拟机菜单,有安装vmware tools 工具的选项 点击之后,在Linux的桌面下会出现 VMwareTools. ...