机器学习作业(五)机器学习算法的选择与优化——Matlab实现
题目下载【传送门】
第1步:读取数据文件,并可视化:
% Load from ex5data1:
% You will have X, y, Xval, yval, Xtest, ytest in your environment
load ('ex5data1.mat'); % m = Number of examples
m = size(X, 1); % Plot training data
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
运行结果:
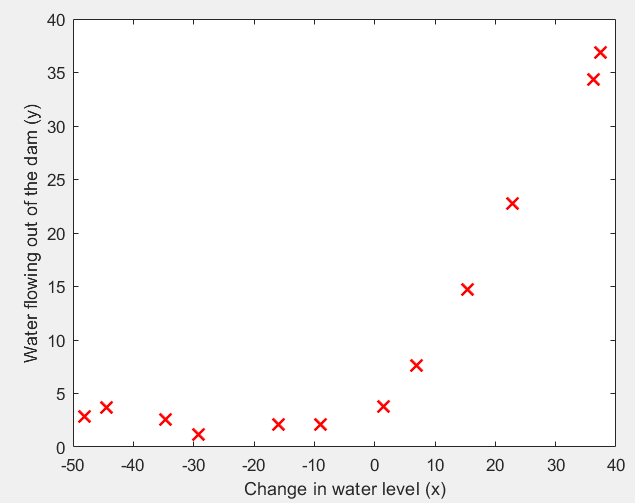
第2步:实现linearRegCostFunction函数,采用线性回归和正规化求 J 和 grad:
function [J, grad] = linearRegCostFunction(X, y, theta, lambda) % Initialize some useful values
m = length(y); % number of training examples % You need to return the following variables correctly
J = 0;
grad = zeros(size(theta)); theta_copy = theta;
theta_copy(1, :) = 0
J = 1 / (2 * m) * sum((X * theta - y) .^ 2) + lambda / (2 * m) * sum(theta_copy .^ 2);
grad = 1 / m * (X' * (X * theta - y)) + lambda / m * theta_copy; grad = grad(:); end
第3步:实现训练函数trainLinearReg:
function [theta] = trainLinearReg(X, y, lambda) % Initialize Theta
initial_theta = zeros(size(X, 2), 1); % Create "short hand" for the cost function to be minimized
costFunction = @(t) linearRegCostFunction(X, y, t, lambda); % Now, costFunction is a function that takes in only one argument
options = optimset('MaxIter', 200, 'GradObj', 'on'); % Minimize using fmincg
theta = fmincg(costFunction, initial_theta, options); end
使用 lambda = 0,测试结果:
% Train linear regression with lambda = 0
lambda = 0;
[theta] = trainLinearReg([ones(m, 1) X], y, lambda); % Plot fit over the data
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
hold on;
plot(X, [ones(m, 1) X]*theta, '--', 'LineWidth', 2)
hold off;
运行结果:很显然,采用 y = θ0 + θ1x 欠拟合。
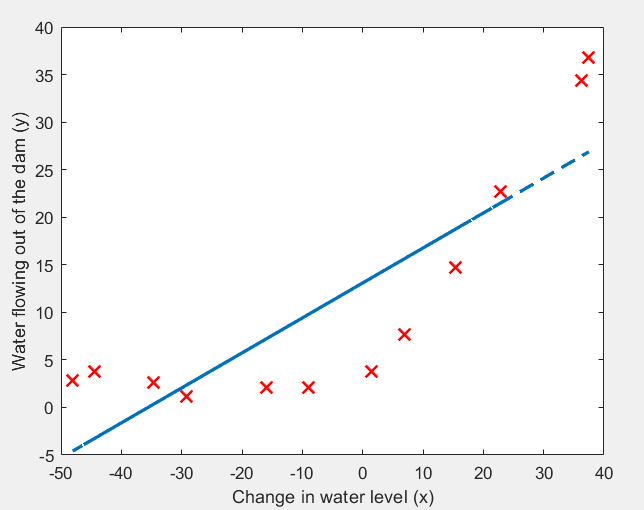
第4步:绘制关于训练集数量的学习曲线,在lambda = 0 的情况下,观察训练集的大小1 ~ m给训练误差和验证误差的影响:
lambda = 0;
[error_train, error_val] = ...
learningCurve([ones(m, 1) X], y, ...
[ones(size(Xval, 1), 1) Xval], yval, ...
lambda); plot(1:m, error_train, 1:m, error_val);
title('Learning curve for linear regression')
legend('Train', 'Cross Validation')
xlabel('Number of training examples')
ylabel('Error')
axis([0 13 0 150])
其中学习曲线函数learningCurve:
function [error_train, error_val] = ...
learningCurve(X, y, Xval, yval, lambda) for i = 1:m,
X_temp = X(1:i, :);
y_temp = y(1:i);
theta = trainLinearReg(X_temp, y_temp, lambda);
error_train(i) = 1 / (2 * i) * sum((X_temp * theta - y_temp) .^ 2);
error_val(i) = 1 / (2 * m) * sum((Xval * theta - yval) .^ 2);
end end
运行结果:随着训练集的扩大,训练误差和验证误差均比较大,是高误差问题(欠拟合)。
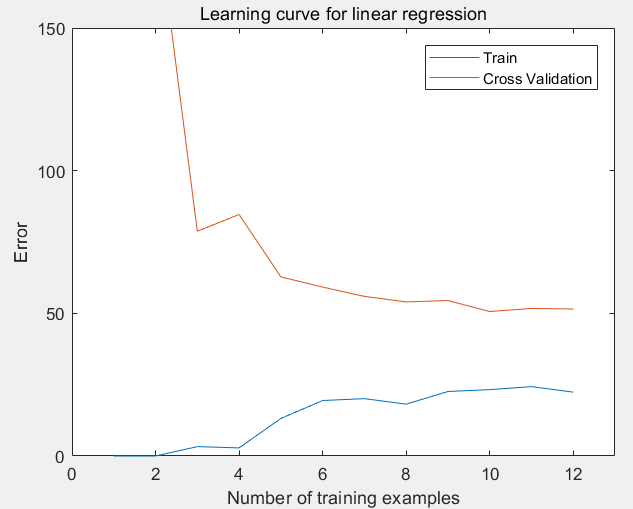
第5步:为了解决欠拟合问题,需要改进特征,下面对训练、交叉验证、测试三组数据进行特征扩充和均值归一化:
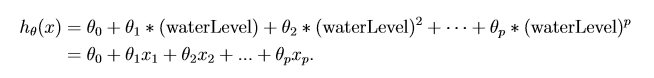
p = 8; % Map X onto Polynomial Features and Normalize
X_poly = polyFeatures(X, p);
[X_poly, mu, sigma] = featureNormalize(X_poly); % Normalize
X_poly = [ones(m, 1), X_poly]; % Add Ones % Map X_poly_test and normalize (using mu and sigma)
X_poly_test = polyFeatures(Xtest, p);
X_poly_test = bsxfun(@minus, X_poly_test, mu);
X_poly_test = bsxfun(@rdivide, X_poly_test, sigma);
X_poly_test = [ones(size(X_poly_test, 1), 1), X_poly_test]; % Add Ones % Map X_poly_val and normalize (using mu and sigma)
X_poly_val = polyFeatures(Xval, p);
X_poly_val = bsxfun(@minus, X_poly_val, mu);
X_poly_val = bsxfun(@rdivide, X_poly_val, sigma);
X_poly_val = [ones(size(X_poly_val, 1), 1), X_poly_val]; % Add Ones fprintf('Normalized Training Example 1:\n');
fprintf(' %f \n', X_poly(1, :));
其中ployFeatures函数实现特征值扩充的作用:
function [X_poly] = polyFeatures(X, p) % You need to return the following variables correctly.
X_poly = zeros(numel(X), p); X_poly(:, 1) = X(:, 1);
for i = 2:p,
X_poly(:, i) = X_poly(:, i-1) .* X(:, 1);
end end
其中featureNormalize函数实现均值归一化功能:
function [X_norm, mu, sigma] = featureNormalize(X) mu = mean(X);
X_norm = bsxfun(@minus, X, mu); sigma = std(X_norm);
X_norm = bsxfun(@rdivide, X_norm, sigma); end
第6步:设置不同的lambda,查看拟合结果和学习曲线:
lambda = 0;
[theta] = trainLinearReg(X_poly, y, lambda); % Plot training data and fit
figure(1);
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
plotFit(min(X), max(X), mu, sigma, theta, p);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
title (sprintf('Polynomial Regression Fit (lambda = %f)', lambda)); figure(2);
[error_train, error_val] = ...
learningCurve(X_poly, y, X_poly_val, yval, lambda);
plot(1:m, error_train, 1:m, error_val); title(sprintf('Polynomial Regression Learning Curve (lambda = %f)', lambda));
xlabel('Number of training examples')
ylabel('Error')
axis([0 13 0 100])
legend('Train', 'Cross Validation')
(1)lambda = 0的情况:过拟合
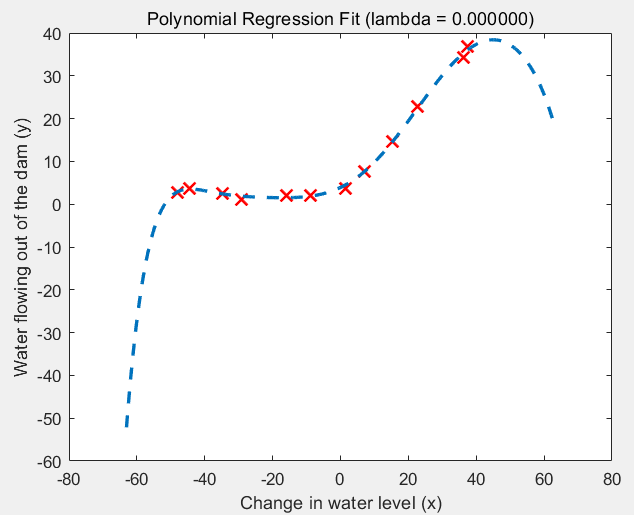
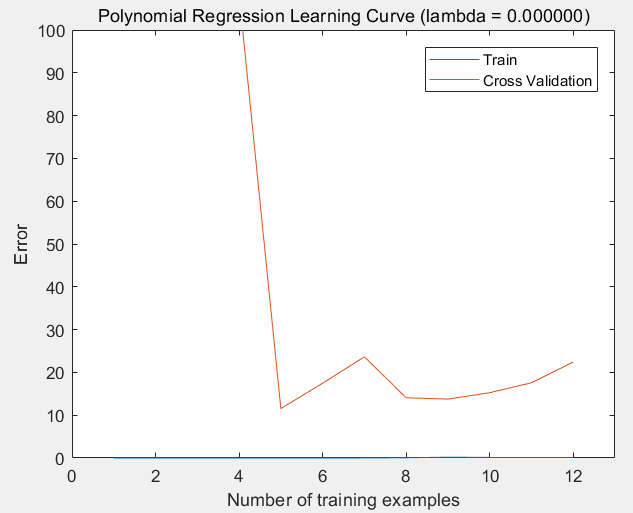
(2)lambda = 1的情况:过拟合
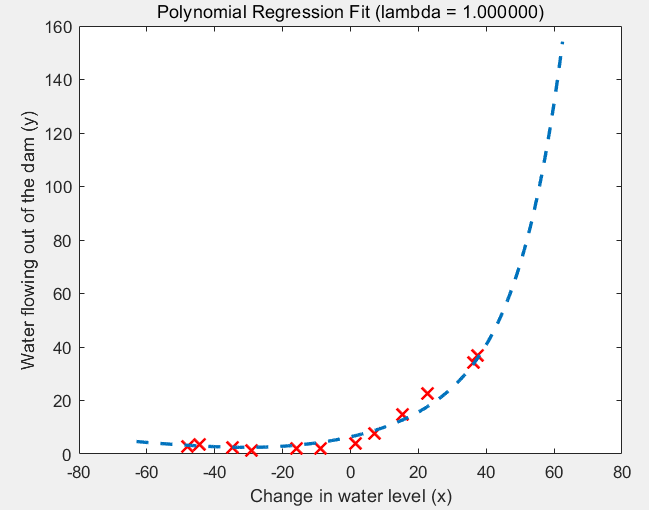
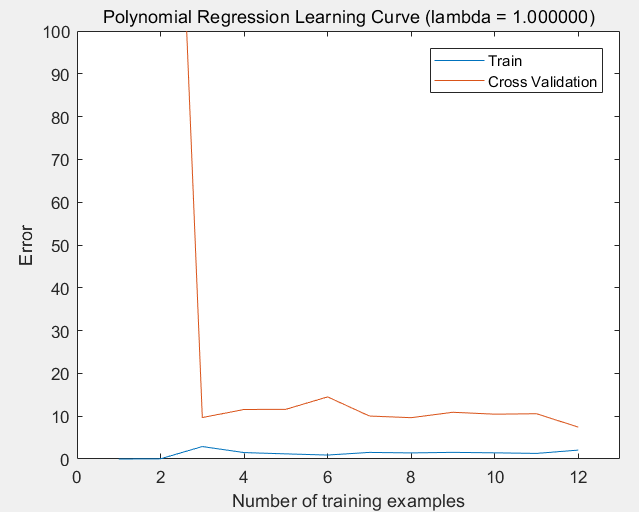
(3)lambda = 100的情况:欠拟合
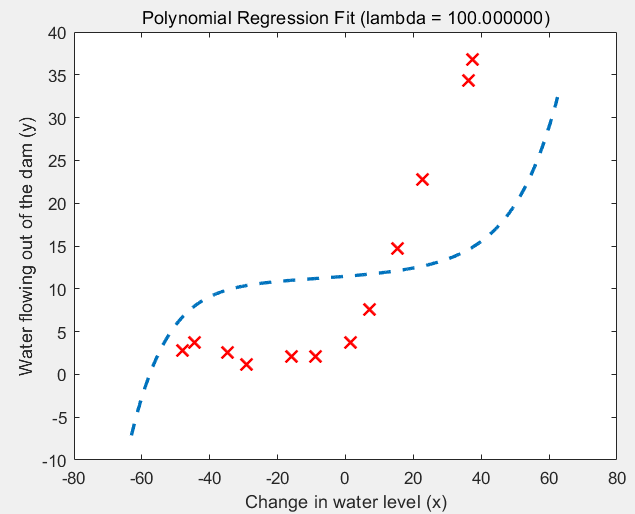
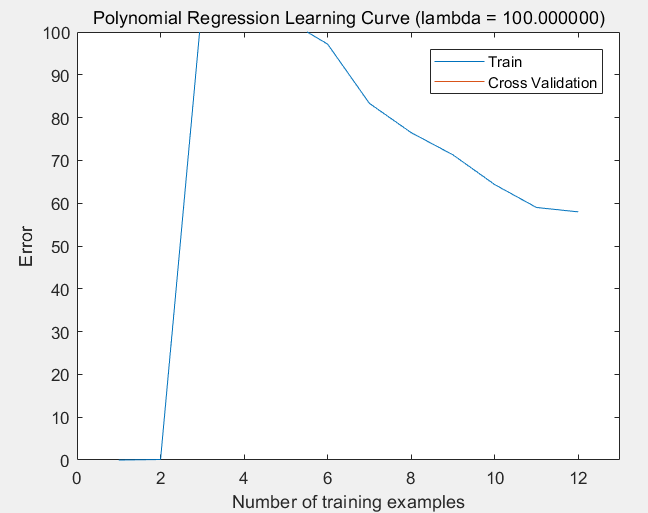
第7步:绘制关于lambda的学习曲线,选择最优的lambda:
[lambda_vec, error_train, error_val] = ...
validationCurve(X_poly, y, X_poly_val, yval); close all;
plot(lambda_vec, error_train, lambda_vec, error_val);
legend('Train', 'Cross Validation');
xlabel('lambda');
ylabel('Error');
其中validationCurve函数:
function [lambda_vec, error_train, error_val] = ...
validationCurve(X, y, Xval, yval) m = size(X, 1)
for i = 1:size(lambda_vec),
lambda = lambda_vec(i);
theta = trainLinearReg(X, y, lambda);
error_train(i) = 1 / (2 * m) * sum((X * theta - y) .^ 2);
error_val(i) = 1 / (2 * m) * sum((Xval * theta - yval) .^ 2);
end end
运行结果:可以看出,在lambda在[2, 3]上有较好的效果。
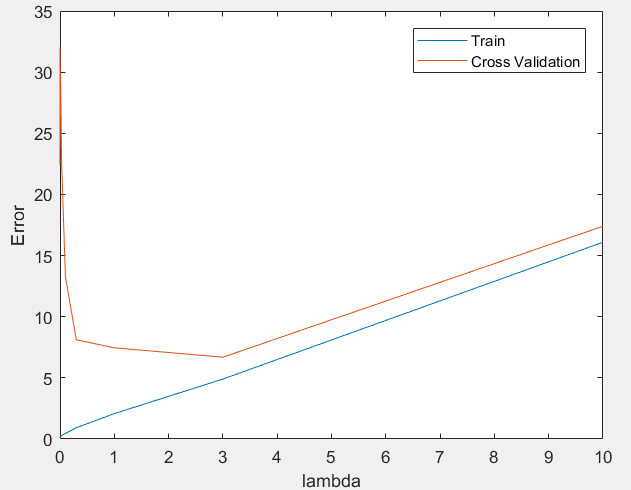
机器学习作业(五)机器学习算法的选择与优化——Matlab实现的更多相关文章
- 机器学习作业(八)异常检测与推荐系统——Matlab实现
题目下载[传送门] 第1题 简述:对于一组网络数据进行异常检测. 第1步:读取数据文件,使用高斯分布计算 μ 和 σ²: % The following command loads the datas ...
- 机器学习作业(四)神经网络参数的拟合——Matlab实现
题目下载[传送门] 题目简述:识别图片中的数字,训练该模型,求参数θ. 第1步:读取数据文件: %% Setup the parameters you will use for this exerci ...
- python机器学习笔记:EM算法
EM算法也称期望最大化(Expectation-Maximum,简称EM)算法,它是一个基础算法,是很多机器学习领域的基础,比如隐式马尔科夫算法(HMM),LDA主题模型的变分推断算法等等.本文对于E ...
- 机器学习五 -- 机器学习的“Hello World”,感知机
机器学习五 -- 机器学习的“Hello World”,感知机 感知机是二类分类的线性分类模型,是神经网络和支持向量机的基础.其输入为实例的特征向量,输出为实例的类别,取+1和-1二值之一,即二类分类 ...
- 机器学习中的K-means算法的python实现
<机器学习实战>kMeans算法(K均值聚类算法) 机器学习中有两类的大问题,一个是分类,一个是聚类.分类是根据一些给定的已知类别标号的样本,训练某种学习机器,使它能够对未知类别的样本进行 ...
- 机器学习:K-近邻算法(KNN)
机器学习:K-近邻算法(KNN) 一.KNN算法概述 KNN作为一种有监督分类算法,是最简单的机器学习算法之一,顾名思义,其算法主体思想就是根据距离相近的邻居类别,来判定自己的所属类别.算法的前提是需 ...
- 机器学习入门:K-近邻算法
机器学习入门:K-近邻算法 先来一个简单的例子,我们如何来区分动作类电影与爱情类电影呢?动作片中存在很多的打斗镜头,爱情片中可能更多的是亲吻镜头,所以我们姑且通过这两种镜头的数量来预测这部电影的主题. ...
- 机器学习之决策树(ID3)算法与Python实现
机器学习之决策树(ID3)算法与Python实现 机器学习中,决策树是一个预测模型:他代表的是对象属性与对象值之间的一种映射关系.树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每 ...
- 机器学习之路--KNN算法
机器学习实战之kNN算法 机器学习实战这本书是基于python的,如果我们想要完成python开发,那么python的开发环境必不可少: (1)python3.52,64位,这是我用的python ...
随机推荐
- Git操作:一次性强制push所有分支
现在手上有两个分支,master和rotation,想一次性推送所有分支,可以用--all参数来实现: git push --all origin 如果远程仓库有更改,但你需要直接推送,那就可以使用强 ...
- Windows2008R2 一键安全优化脚本
::author vim ::QQ 82996821 ::filename Windows2008R2_safe_auto_set.bat :start @echo off color 0a ...
- Python 使用OS模块调用 cmd
在os模块中提供了两种调用 cmd 的方法,os.popen() 和 os.system()os.system(cmd) 是在执行command命令时需要打开一个终端,并且无法保存command命令的 ...
- 面向对象+闭包+三种对象的声明方式(字面式、new Object、构造函数、工厂模式、原型模式、混合模式)
面向对象: 对代码的一种抽象,对外统一提供调用接口的编程思想 对象的属性:事物自身拥有的东西 对象的方法:事物的功能 对象:事物的一个实例 对象的原型:.prototype -> 内存地址 -& ...
- go 网络编程
网络编程 tcp 1.tcp客户端服务端实现 server/server.go package main import ( "fmt" "net" ) /* t ...
- Go 与 PHP 的语法对比
Go 是由 Google 设计的一门静态类型的编译型语言.它有点类似于 C,但是它包含了更多的优点,比如垃圾回收.内存安全.结构类型和并发性.它的并发机制使多核和网络机器能够发挥最大的作用.这是 Go ...
- windows server2008 IIS下目录 [ application/database.php ] 不可写!解决
windows server2008目录 [ application/database.php ] 不可写!解决 在服务器上找到网站根目录 网站用的thinkphp的框架 属性 -- ...
- BLOB-数据库中用来存储二进制文件的字段类型
BLOB (binary large object)----二进制大对象,是一个可以存储二进制文件的容器. 在计算机中,BLOB常常是数据库中用来存储二进制文件的字段类型. BLOB是一个大文件,典型 ...
- Wannafly Winter Camp 2020 Day 7E 上升下降子序列 - 数学
神奇公式 #include <bits/stdc++.h> using namespace std; #define int long long int n,mod,c[205][205] ...
- get请求与post请求中文乱码问题的解决办法
首先出现中文乱码的原因是tomcat默认的编码方式是"ISO-8859-1",这种编码方式以单个字节作为一个字符,而汉字是以两个字节表示一个字符的. 一,get请求参数中文乱码的解 ...
