AcWing 873. 欧拉函数

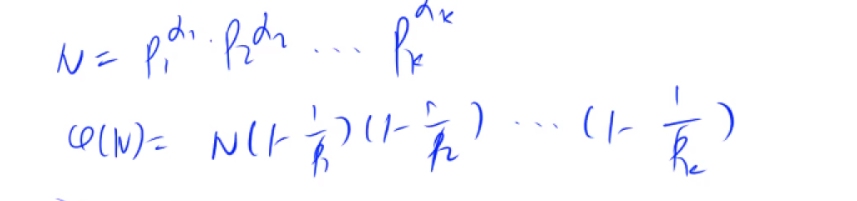
//用定义直接求
#include<bits/stdc++.h>
using namespace std;
int main() {
    int n;
    cin>>n;
    while(n--) {
        int x;
        cin>>x;
        int res=x;
        for(int i=; i<=x/i; i++) {
            if(x%i==) {
                res=res/i*(i-);   //防止溢出
                while(x%i==) x/=i;
            }
        }
        if(x>) res=res/x*(x-);
        cout<<res<<endl;
    }
    return ;
}