Linux（9.28-10.4）学习笔记

三种数字表示

无符号数：

基于传统的二进制表示法，表示大于或者等于零的数字。

补码（有符号数）：

表示有符号数整数的最常见的方式，有符号数就是只可

以为正或者为负的数。

浮点数：

表示实数的科学计数法的以二为基数的版本。

进制转换

      以二进制和十进制为桥梁进行转换

0x与0X用来表示十六进制

字

字长指明整数和指针数据的标称大小，决定虚拟地址空间的最大大小。       对于一个字长为w位的机器，虚拟地址的范围为0 ~2^w - 1,程序最多访问2^w个字节。

数据大小

gcc -m32 可以在64位机上生成32位的代码

c语言中数字数据类型的字节数

C声明	32位机器	64位机器
Char	1	1
Short int	2	2
Int	4	4
Long int	4	8
Long long int	8	8
Char*	4	8
Float	4	4
Double	8	8

寻址和字节顺序

小端法

       在存储器中按照从最低有效字节到最高有效字节的顺序存储对象。

大端法

       从最高有效字节到最低有效字节的顺序存储。

（小端法：高对高，低对低。大端法：高对低，低对高。）

书28页代码

 

 表示字符串

ASCⅡ字符码

a-z的ASC||码为0x61-0x7A。

表示代码

二进制代码是不兼容的。

布尔代数

二进制值是计算机编码、存储、操作信息的核心（0、1）

逻辑运算——0或1

位运算————位向量

~=NOT

&=AND

|=OR

^=异或

*位向量：有固定长度为w，由0、1组成的串。每个对应元素之间的运算。 掩码。通过指定一个位向量掩码，有选择的使能或不能屏蔽一些信号。（0表示被屏蔽）

C语言中的位级运算

|是OR（或）

&是AND（与）

~是NOT（取反）

^是EXCLUSIVE-OR（异或）

确定一个位级表达式的结果最好的方法，就是将十六进制的参数扩展成二进制标识并执行二进制运算，然后再转换回十六进制。

C语言中的逻辑运算

|| OR

&& AND

！ NOT

所有非零的参数表示TRUE

参数0表示FALSE

它们返回1或者0，分别表示结果为TRUE或FALSE

C语言中的移位运算

1.左移(x<<k) x向左移动k位，丢弃最高的k位，并在右端补k个0

2.右移(x>>k) 逻辑右移：x向右移动k位，丢弃最高的k位，并在左端补k个0.

算术右移：x向右移动k位，丢弃最高的k位，并在左端补k个最高有效为的值。

对于无符号数据，右移必须是逻辑的。对于有符号数，算术或逻辑右移均可以。

整数的表示

具体数据类型的表示范围在教材P38

要用C99中的"long long"类型，编译要用gcc -std=c99

无符号数的编码：

数据类型long long是在ISO C99中引入的。（编译：gcc -std=c99）。

64位机器用8个字节表示；32位机器用4个字节表示。

*负数的范围比整数的范围大1。

补码编码：

最常见的有符号数的计算机表示方式。

正数的补码=原码

负数的补码=原码各位取反再加1

最高有效位也叫符号位。

补码的范围是不对称的：|TMin| = |TMax| + 1，也就是说，TMin没有

与之对应的正数。

补码的利用寄存器的长度是固定的特性简化数学运算。想想钟表，12-1
等价于 12 + 11，利用补码可以把数学运算统一成加法，只要一个加法器
就可以实现所有的数学运算。（应正确理解补码）

有符号数和无符号数之间的转换

强制类型转换的结果保持位值不变，改变解释这些位的方式。 处理同样字长的有、无符号数之间相互转换的规则：数值可能会变，但是位模式不变。

（底层的位表示保持不变） 无————>有：U2Tw函数 有————>无：T2Uw函数

有符号数与无符号数之间的转换，都要看要转换的数的最高位是否为1，如果不为1，则转换结果就是要转换的数的本身；

如果为1，则转换结果就是转换的数（看作是负数）的补码。

C语言中的有符号数与无符号数

当C语言对同时包含有符号和无符号数表达式执行运算时，会将有符号数强制转换为无符号数，再进行运算。

扩展一个数字的位表示

零扩展：

将一个无符号数转换为一个更大的数据类型，我们只需要简单地在表示的开头添加0。

符号扩展：

将一个补码数字转换为一个更大的数据类型可以执行符号扩展（sign extension），规则是在表示中添加最高有效位的值的副本。

 

整数运算

无符号加法

         w表示最大表示位，当x+y>2^w-1，其和溢出

补码加法

补码的非

无符号乘法

w位无符号乘法运算* wu的结果为：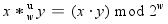

补码乘法

C语言中的有符号乘法是通过将2^w位的乘积截断为w位的方式实现的。

根据等式，w位的补码乘法运算* wt的结果为：

除以2的幂

无符号数除以2的幂

	x>>k等价于x/(2^k)

有符号数除以2的幂

	1.非负数同无符号数

	2.x>>k（算术右移），结果同除以2的幂几乎完全一样

浮点数
1.二进制小数
	定点表示法：“.”为界（不能有效的表示很大的数）
十进制
	小数点左边的数字的权是10的非负幂，得到整数值；右边的数字的权是10的负幂，得到小数值。
二进制
	小数点左边的数字的权是2的非负幂，右边的数字的权是2的负幂。
2.IEEE浮点表示
1.用V = (-1)s * M * 2E的形式来表示一个数：
符号
	s决定这个数是负数（s = 1）还是正数（s = 0），而对于数值0的符号位解释作为特殊情况处理。
尾数
	M是一个二进制小数，它的范围是1 ~ 2-ε，或者是0 ~ 1-ε。 
阶码
	E的作用是对浮点数据加权，这个权重是2的E次幂（可能是负数）。
2.将浮点数的位表示划分为三个字段，分别对这些值进行编码：
	一个单独的符号位s直接编码符号s。
	k位的阶码字段exp = ek-1…e1e0编码阶码E。
	n位小数字段frac = fn-1…f1f0编码尾数M，但是编码出来的值也依赖于阶码字段的值是否等于0。
3.两种常见的格式
	C语言中的单精度浮点格式float 和双精度浮点格式double。
	在float中，s、exp和frac字段分别为1位、k = 8 位和n = 23位，得到一个32位的表示；
	在double中，s、exp和frac字段分别为1位、k = 11 位和n = 52位，得到一个64位的表示。


遇到的问题
	1.IEEE浮点表示方法由于第一次接触，明显觉得很难理解.记忆 2.在做第28页习题是，感觉gcc及 gdb运用很生涩浪费了很多时间