POJ1737 Connected Graph

Connected Graph

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 3156		Accepted: 1533

Description

An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.

For example,there are 4 different connected undirected graphs with 3 vertices.

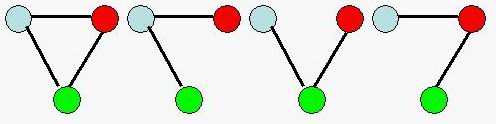
Input

The
input contains several test cases. Each test case contains an integer n,
denoting the number of vertices. You may assume that 1<=n<=50.
The last test case is followed by one zero.

Output

For each test case output the answer on a single line.

Sample Input

1
2
3
4
0

Sample Output

1
1
4
38

Source

LouTiancheng@POJ

 

 

 

n个点之间任取两点连边，按照组合数公式，共有$ C(n,2)=n*(n-1)/2 $条边可连

每条边可连可不练，所以总情况有 P=2^C(n,2) 种。

我们要求的是所有点都连通的情况数，可以用总数P减去不连通的情况数

设F[i]为i个点构成连通图的情况数，任取一点为基准，当与其构成连通图的点有j-1个时，共有F[j]种连通情况。则若在总图中有j个点一定连通，共有$C(i-1,j-1)*F[j] $种情况,而剩下的点可以随意连边，共有$2^C(i-j,2)$种情况。

若总点数为i，则答案为:$F[i]=P[i]-sum$;   sum=sum+(C(i-1,j-1)*F[j]*2^C(i-j,2))    {1<=j<i 累加求和}

 

然而高精度各种写不对，我选择死亡。

 

先放一张表

 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT:
 INPUT:
 OUTPUT: 

打表

然后是我一直改不对的代码

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 struct bgnum{
     int l;
     int a[];
     bgnum operator + (const bgnum &x) const{
         bgnum ans;
         memset(ans.a,,sizeof(ans.a));
         int len=max(l,x.l);
         ans.l=;
         for(int i=;i<=len;i++){
             ans.a[i]+=a[i]+x.a[i];
             ans.a[i+]+=ans.a[i]/;
             ans.a[i]%=;

         }
         len++;
         while(!ans.a[len]&&len)len--;
         ans.l=len;
         return ans;
     }
     bgnum operator - (const bgnum &x) const{
         bgnum ans;
         memset(ans.a,,sizeof(ans.a));
         for(int i=;i<=l;i++){
             ans.a[i]+=a[i]-x.a[i];
             if(ans.a[i]<){
                 ans.a[i]+=;
                 ans.a[i-]--;
             }
         }
         ans.l=l;
         while(!ans.a[ans.l] && ans.l) ans.l--;
         return ans;
     }
     bgnum operator * (const bgnum &x) const{
         bgnum ans;
         memset(ans.a,,sizeof(ans.a));
         for(int i=;i<=l;i++)
             for(int j=;j<=x.l;j++){
                 ans.a[i+j-]+=a[i]*x.a[j];
                 ans.a[i+j]+=ans.a[i+j-]/;
                 ans.a[i+j-]%=;
             }
         int len=l+x.l;
         while(!ans.a[len] && len)len--;
         ans.l=len;
         return ans;
     }
 }f[],//[i]个点构不同图的方案数
  c[][],//[i]个点中选[j]个任意连边的方案数
  mi[],//2的[i]次方
  sum;

 void Print(bgnum p){
     for(int i=p.l;i>=;i--){
         printf("%d",p.a[i]);
     }
     printf("\n");
     return;
 }
 bgnum p1,p2;
 int main(){
     p1.l=;p1.a[]=;//高精度数1
     p2.l=;p2.a[]=;//高精度数2
     int i,j;
     mi[]=p1;
     for(i=;i<=;i++)
         mi[i]=mi[i-]*p2;
     for(i=;i<=;i++)
         c[i][]=p1;
     for(i=;i<=;i++)
         for(j=;j<=i;j++){
             c[i][j]=c[i-][j]+c[i-][j-];//组合数递推公式
         }
     for(i=;i<=;i++){
         sum.l=;
         memset(sum.a,,sizeof(sum.a));
         for(j=;j<i;j++){
             sum=sum+(c[i-][j-]*f[j]*mi[(i-j)*(i-j-)/]);
         }
 //        Print(sum);
         f[i]=mi[i*(i-)/]-sum;
     }
     int n;
     scanf("%d",&n);
     Print(f[n]);
     return ;
 }

再放隔壁某dalao的AC题解

http://blog.csdn.net/orion_rigel/article/details/51812864