判断一个点在多边形的内部C++

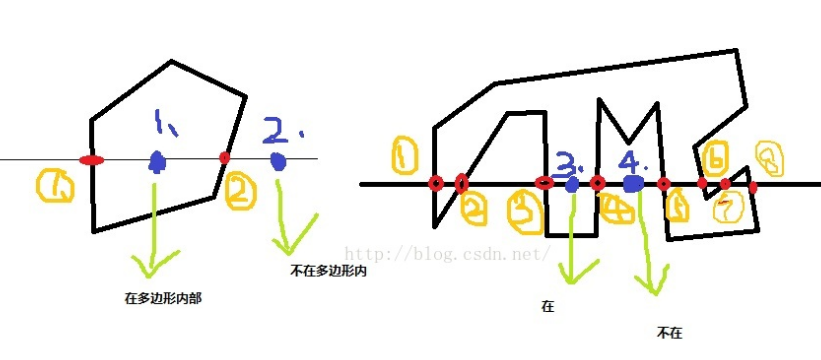
 /* 原理: 将测试点的Y坐标与多边形的每一个点进行比较，
 **    会得到测试点所在的行与多边形边的所有交点。
 **    如果测试点的两边点的个数都是奇数个，
 **    则该测试点在多边形内，否则在多边形外。 */
 #include <stdio.h>
 #include <iostream>
 /* 函数功能: 判断点(x, y)是否在有ploy_sides个顶点的多边形内 */
 /* 参数: poly_sides    测试多边形的顶点数
 **    poly_x    测试多边形的各个顶点的X轴坐标
 **    poly_y    测试多边形的各个顶点的Y轴坐标
 **    x    测试点的X轴坐标
 **    Y 测试点的Y轴坐标 */
 /* 返回值: 返回0 表示不在多边形内部，返回1 表示在多边形内部 */
 /* 说明: 在多边形各边上的点默认不在多边形内部 */
 int inOrNot(int poly_sides, float *poly_X, float *poly_Y, float x, float y)
 {
     int i, j;
     j = poly_sides - ;
     int res = ;
     for (i = ; i<poly_sides; i++)
     {
         //对每一条边进行遍历，该边的两个端点，有一个必须在待检测点(x,y)的左边，且两个点中，有一个点的y左边比p.y小，另一个点的y比p.y大。
         if ((poly_Y[i]<y && poly_Y[j] >= y || poly_Y[j]<y && poly_Y[i] >= y) && (poly_X[i] <= x || poly_X[j] <= x))
         {
             //用水平的直线与该边相交，求交点的x坐标。
             res ^= ((poly_X[i] + (y - poly_Y[i]) / (poly_Y[j] - poly_Y[i])*(poly_X[j] - poly_X[i])) < x);
         }
         j = i;
     }
     return res;
 }
 
 int main(void)
 {
     int poly_sides = ;    // 多边形顶点数
     float poly_X[] = { , , , ,  };    // 多边形各顶点的X轴坐标
     float poly_Y[] = { , , , ,  };    // 多边形各顶点的Y轴坐标
     float x = ;    // 测试点的X轴坐标
     float y = ; // 测试点的Y轴坐标
     int ret;
     ret = inOrNot(poly_sides, poly_X, poly_Y, x, y);
     if ( == ret)
     {
         printf("the point (%f, %f), in the poly\n", x, y);
     }
     else
     {
         printf("the point (%f, %f), not in the poly\n", x, y);
     }
     system("pause");
     return ;
 }