时间序列模式（ARIMA）---Python实现

时间序列分析的主要目的是根据已有的历史数据对未来进行预测。如餐饮销售预测可以看做是基于时间序列的短期数据预测，预测的对象时具体菜品的销售量。

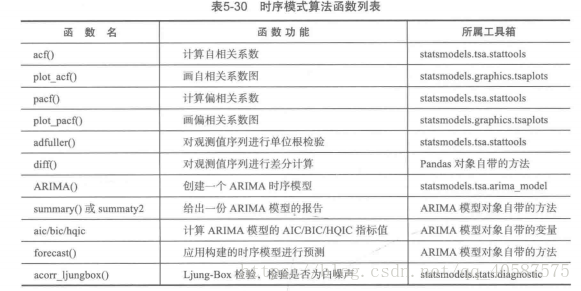
1.时间序列算法：

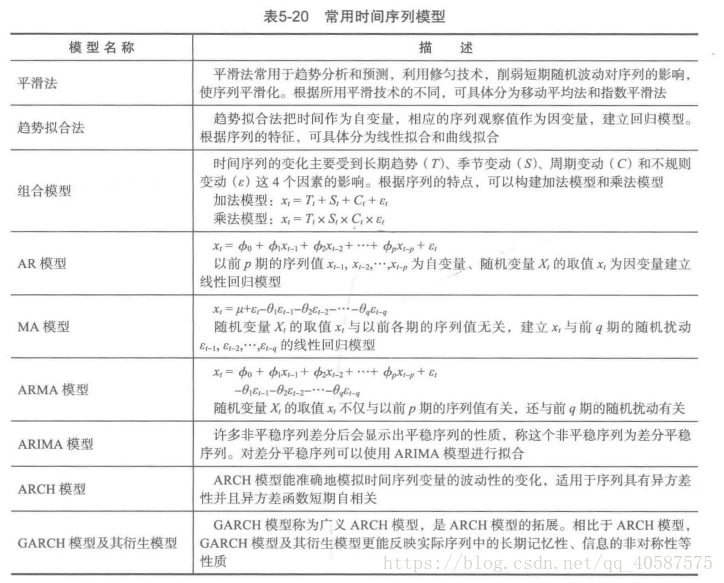
常见的时间序列模型;

2.时序模型的预处理

1. 对于纯随机序列，也称为白噪声序列，序列的各项之间没有任何的关系，序列在进行完全无序的随机波动，可以终止对该序列的分析。

2. 对于平稳非白噪声序列，它的均值和方差是常数。ARMA 模型是最常用的平稳序列拟合模型。

3. 对于非平稳序列，由于它的方差和均值不稳定，处理方法一般是将其转化成平稳序列。可以使用ARIMA 模型进行分析。

对平稳性的检验：

1.时序图检验：根据平稳时间序列的均值和方差都是常数的特性，平稳序列的时序图显示该序列值时钟在一个参数附近随机波动，而且波动的范围是有界的。如果有明显的趋势或者周期性，那它通常不是平稳序列。

2.自相关图检验：平稳序列具有短期相关性，这个性质表明对平稳序列而言，通常只有近期的序列值得影响比较明显，间隔越远的过去值对现在的值得影响越小。而非平稳序列的自相关系数衰减的速度比较慢。

3.单位根检验：单位根检验是指检验序列中是否存在单位根，如果存在单位根，那就是非平稳时间序列。目前最常用的方法就是单位根检验。

原假设是非平稳序列过程，备择假设是平稳序列，趋势平稳过程

上述参考：百度文库

3.时间序列分析：

•平稳性：

•平稳性要求经由样本时间序列所得到的拟合曲线，在未来一段时间内仍然沿着现有的形态‘惯性’地延续下去。

•平稳性要求序列的均值和方差不发生明显的变化。

•弱平稳：期望和相关系数（依赖性）不变，未来某个时刻t 的值，Xt 要依赖于它过去的信息。

•差分法：时间序列在 T 与 T-1 时刻的差值（使用差分使其满足平稳性），一般差分1,2 阶就可以了。

•AR（自回归模型）：

•描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。

公式定义：

自回归模型的限制：

1.自回归模型是使用自身的数据进行预测的

2.必须具有平稳性

3.必须具有相关性，如果相关性小于 0.5 ，则不宜使用

4.自回归模型只适用于预测与自身前期相关的预测。

•MA（移动平均模型）：

•移动平均模型关注的是自回归模型中的误差项的累加

•移动平均法能有效地消除预测中的随机波动。

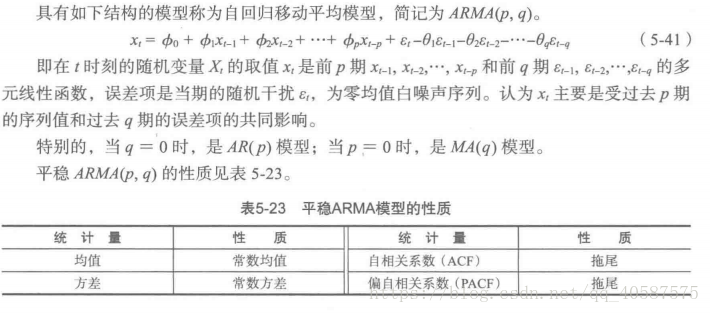
•ARMA（自回归平均模型）：

•自回归和移动平均的结合。

•ARIMA（p,d,q）差分自回归移动平均模型（Autoregressive Integrated Moving Average Model ,简称ARIMA）

•AR 是自回归， p 是自回归项， MA 是移动平均， q 为移动平均项， d 为时间序列称为平稳时所做的差分次数。

•原理：将非平稳时间序列转换成平稳时间序列，然后将因变量仅对它的滞后值（p阶）以及随机误差项的现值和滞后值进行回顾所建立的模型。

•ARIMA 建模流程：

•1.将序列平稳化（差分法确定 d）

•2.p 和 q 阶数的确定（ACF 和 PACF 确定）

•3.建立模型 ARIMA (p , d , q )

使用ARIMA 模型对某餐厅的销售数据进行预测

#使用ARIMA 模型对非平稳时间序列进行建模操作
#差分运算具有强大的确定性的信息提取能力，许多非平稳的序列差分后显示出平稳序列的性质，这是称这个非平稳序列为差分平稳序列。
#对差分平稳序列可以还是要ARMA 模型进行拟合， ARIMA 模型的实质就是差分预算与 ARMA 模型的结合。

#coding=gbk

#使用ARIMA 模型对非平稳时间序列记性建模操作

#差分运算具有强大的确定性的信息提取能力， 许多非平稳的序列差分后显示出平稳序列的性质， 这是称这个非平稳序列为差分平稳序列。

#对差分平稳序列可以还是要ARMA 模型进行拟合， ARIMA 模型的实质就是差分预算与 ARMA 模型的结合。 

#导入数据

import pandas as pd

filename = r'D:\datasets\arima_data.xls'

data = pd.read_excel(filename, index_col = u'日期')

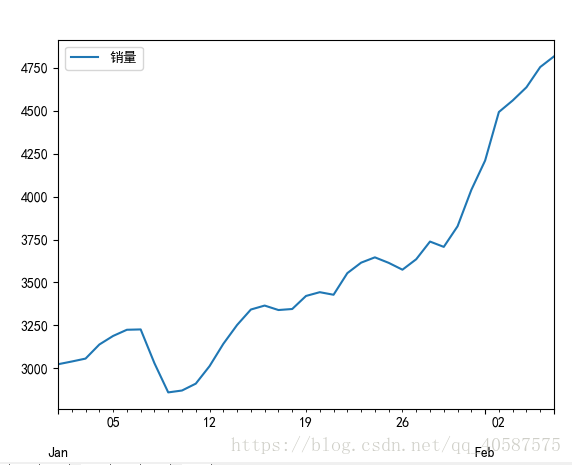
#画出时序图

import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']    #定义使其正常显示中文字体黑体

plt.rcParams['axes.unicode_minus'] = False      #用来正常显示表示负号

# data.plot()

# plt.show()

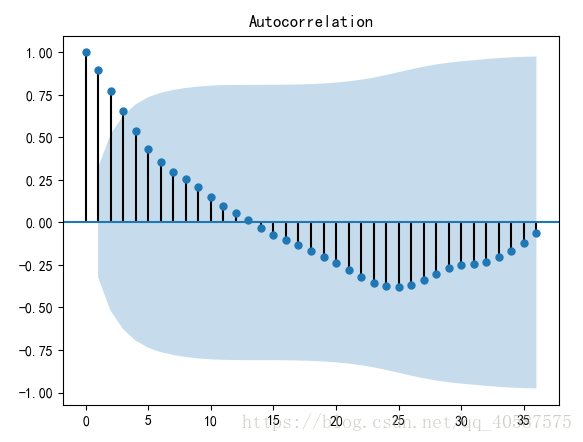
#画出自相关性图

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# plot_acf(data)

# plt.show()

#平稳性检测

from statsmodels.tsa.stattools import adfuller

print('原始序列的检验结果为：',adfuller(data[u'销量']))

#原始序列的检验结果为： (1.8137710150945268, 0.9983759421514264, 10, 26, {'1%': -3.7112123008648155,

#  '10%': -2.6300945562130176, '5%': -2.981246804733728}, 299.46989866024177)

#返回值依次为：adf, pvalue p值， usedlag, nobs, critical values临界值 , icbest, regresults, resstore

#adf 分别大于3中不同检验水平的3个临界值，单位检测统计量对应的p 值显著大于 0.05 ， 说明序列可以判定为 非平稳序列

#对数据进行差分后得到 自相关图和 偏相关图

D_data = data.diff().dropna()

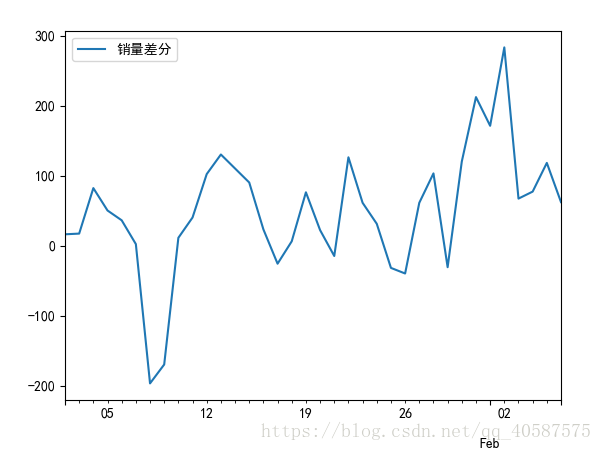
D_data.columns = [u'销量差分']

D_data.plot()   #画出差分后的时序图

# plt.show()

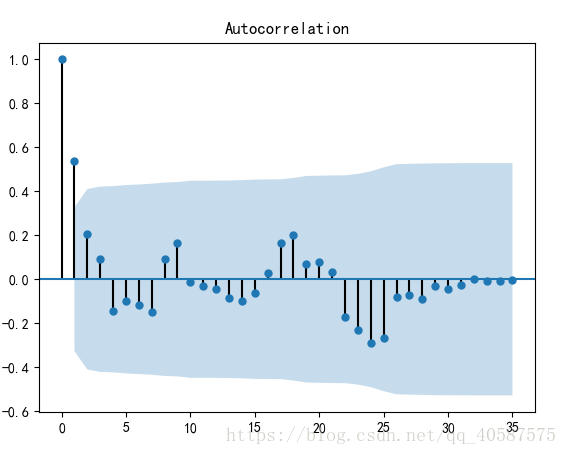
plot_acf(D_data)    #画出自相关图

# plt.show()

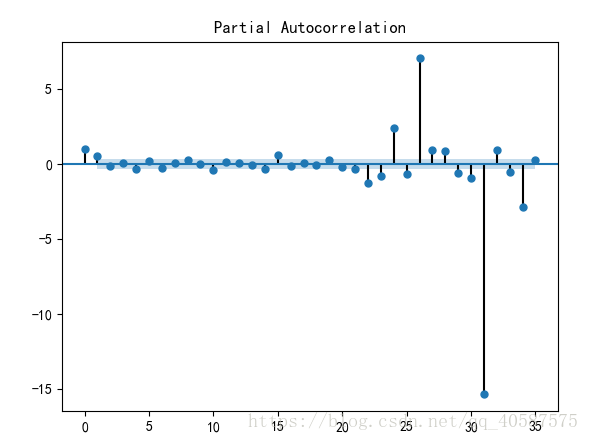
plot_pacf(D_data)   #画出偏相关图

# plt.show()

print(u'差分序列的ADF 检验结果为： ', adfuller(D_data[u'销量差分']))   #平稳性检验

#差分序列的ADF 检验结果为：  (-3.1560562366723537, 0.022673435440048798, 0, 35, {'1%': -3.6327426647230316,

# '10%': -2.6130173469387756, '5%': -2.9485102040816327}, 287.5909090780334)

#一阶差分后的序列的时序图在均值附近比较平稳的波动， 自相关性有很强的短期相关性， 单位根检验 p值小于 0.05 ，所以说一阶差分后的序列是平稳序列

#对一阶差分后的序列做白噪声检验

from statsmodels.stats.diagnostic import acorr_ljungbox

print(u'差分序列的白噪声检验结果：',acorr_ljungbox(D_data, lags= 1)) #返回统计量和 p 值

# 差分序列的白噪声检验结果： (array([11.30402222]), array([0.00077339])) p值为第二项， 远小于 0.05

#对模型进行定阶

from statsmodels.tsa.arima_model import ARIMA 

pmax = int(len(D_data) / 10)    #一般阶数不超过 length /10

qmax = int(len(D_data) / 10)

bic_matrix = []

for p in range(pmax +1):

    temp= []

    for q in range(qmax+1):

        try:

            temp.append(ARIMA(data, (p, 1, q)).fit().bic)

        except:

            temp.append(None)

        bic_matrix.append(temp)

bic_matrix = pd.DataFrame(bic_matrix)   #将其转换成Dataframe 数据结构

p,q = bic_matrix.stack().idxmin()   #先使用stack 展平， 然后使用 idxmin 找出最小值的位置

print(u'BIC 最小的p值 和 q 值：%s,%s' %(p,q))  #  BIC 最小的p值 和 q 值：0,1

#所以可以建立ARIMA 模型，ARIMA(0,1,1)

model = ARIMA(data, (p,1,q)).fit()

model.summary2()        #生成一份模型报告

model.forecast(5)   #为未来5天进行预测， 返回预测结果， 标准误差， 和置信区间

利用模型向前预测的时期越长，预测的误差就会越大，这是时间预测的典型特点。