深度学习课程笔记（四）Gradient Descent 梯度下降算法

深度学习课程笔记（四）Gradient Descent 梯度下降算法

2017.10.06

材料来自：http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS17.html   

我们知道在神经网络中，我们需要求解的是一个最小化的问题，即：最小化 loss function。

假设我们给定一组初始的参数 $\theta$，那么我们可以算出在当前参数下，这个loss是多少，即表示了这个参数到底有多不好。

然后我们利用上述式子来调整参数，其中梯度可以用▽的形式来表示。我们可以将这个过程可视化出来看看：

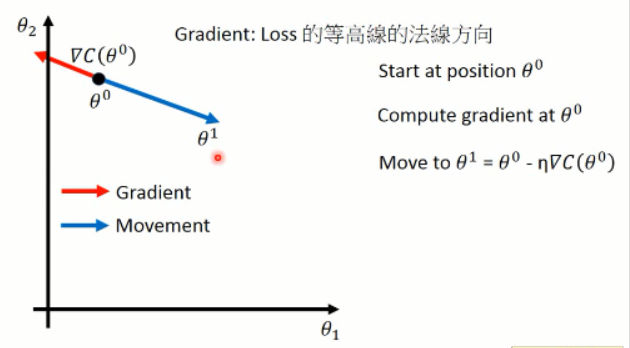
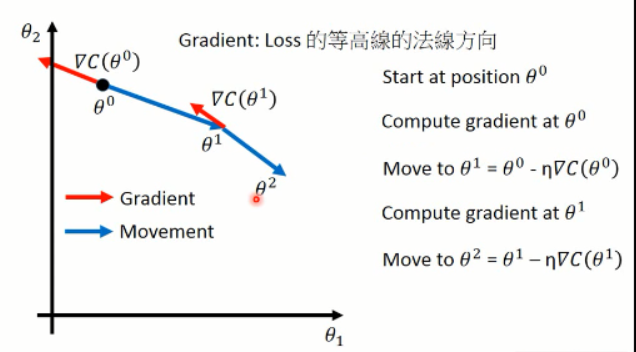
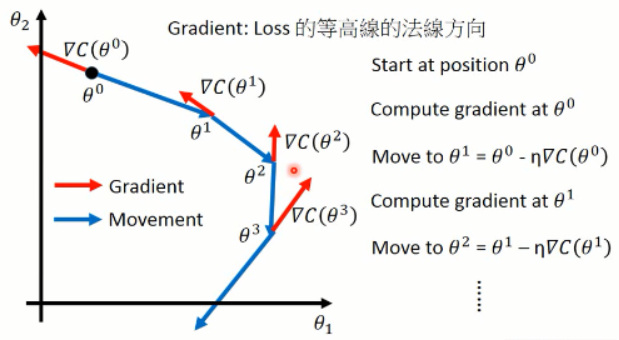
这样子，就算出了每一步当前参数的梯度方向（红色），以及蓝色的调整的方向。这就是梯度下降方法了。

紧接着，李老师讲解了一些梯度下降方法的tips：

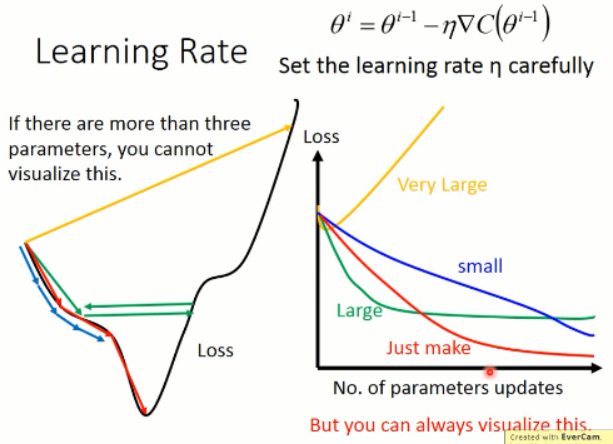
1. 调整你的 学习率（learning rate）：

2. 自适应调整的学习率：

我们可以看到，学习率调整的大原则就是：初始的LR 可以调的很大，因为这个时候我们离局部最小值比较远，当时随着学习的进行，我们需要降低学习率，走的步伐要稍微低一点，因为这个时候我们离目的地已经很近了，我们要微调就行了。否则，就可能错过了最好的点。

我们可以将学习率设置为随着迭代次数变化的变量，这样子就可以自适应的调整 LR了。但是，更好的方式，应该是对于不同的参数，都用不同的学习率来进行优化。其中，这类方法中，最直观最简单的，可能就是 Adagrad了。

这里，李老师给了例子来说明，随着学习的进行，权重的更新是如何自适应变化的。

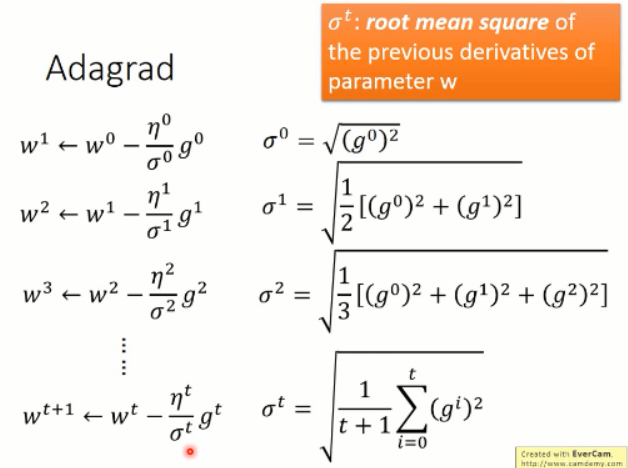
所以，我们将上述式子进一步的化简，可以得到 Adagrad 的参数更新的方程：

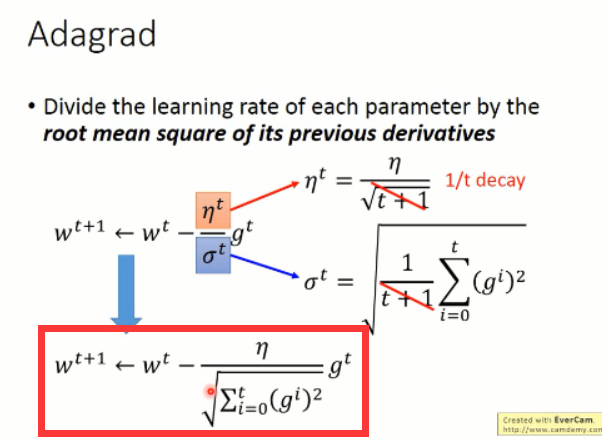
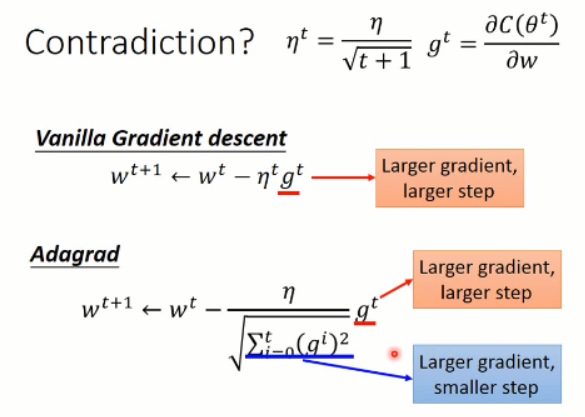
上面就是 Adagrad 方法的全部了，后面李老师对这个更新的方法进行了分析，发现了有如下的看似“不妥当”的东西：当梯度较大的时候，学习的幅度较大，这个没有关系，算是正常；但是，在Adagrad 中，较大的梯度，会导致较大的学习步长，这也没有问题，但是他前面分母当中，较大的梯度，反而使得步长变小了。。。。这又该怎么解释呢？

有一种直观的解释是，这里的 Adagrad 描绘了梯度变化中，反差的情况：

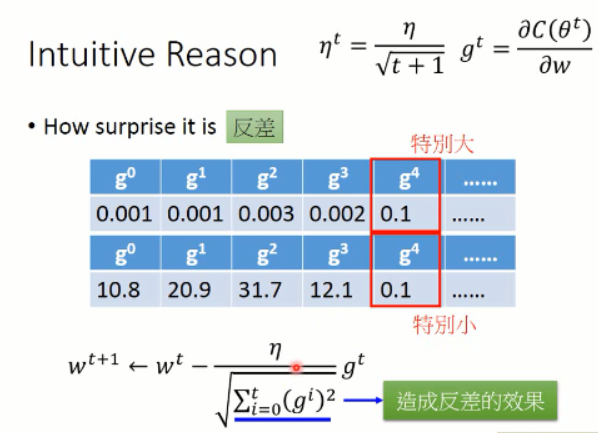
此外，还有另外一种比较正式的解释：

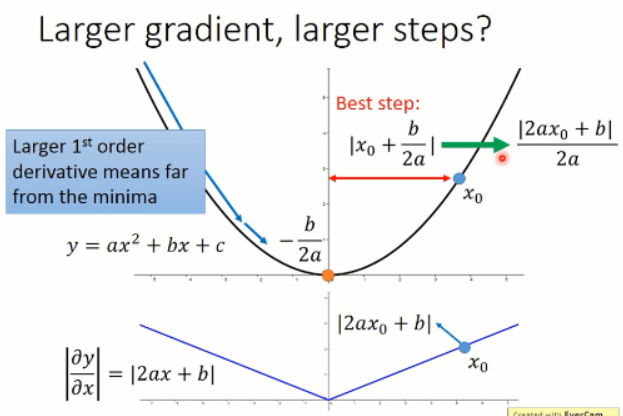
假设我们从 x0 开始出发，我们到最小值处的最优的步长应该是上图中 Best step 所描绘的那样子，而这个值恰好是目标函数微分后的函数在 x0 处的微分值。所以，较好的步长设置应该是 与微分值成正比的一个数字。这是在只考虑一个参数的时候，才成立的。

如果有多个参数，同时影响这个函数的话，情况就很不一样了。此时， gradient 的值越大，那么离局部最小就一定越远，这句话就要打一个问号了。这句话变的不一定成立了。

我们考虑两个参数的情况，w1 and w2 构成下面这样子的梯度情况：

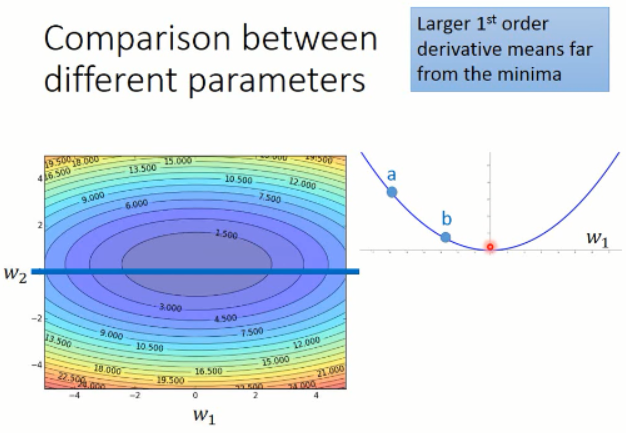
我们在只考虑参数 w1 的情况下，我们可以发现，在 a 点的微分值 是比 b 点的微分值要大的。同时，只对于 w2 来说，也是这样子的。

但是，当跨参数比较的时候，这个结论就不一定成立了。我们来看看下面的这个例子：

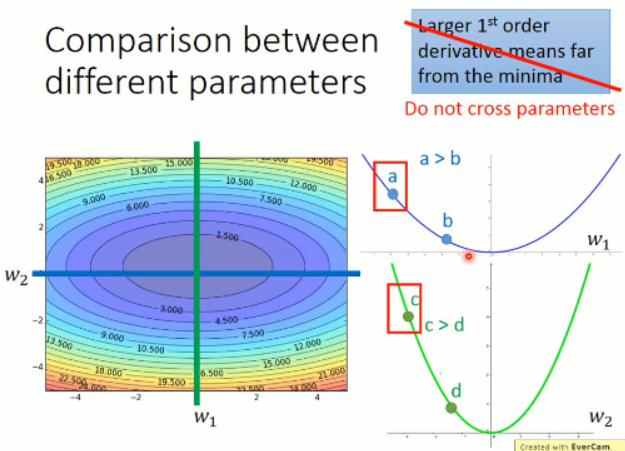
我们来比较下 a 点 和 c点的情况，虽然 c点的梯度比 a点的梯度要大，但是实际上，c点离局部最小值的距离是更近的。所以，梯度大，并不一定离得就远。。。。

比较合理的是，引入二次微分，我们发现最优步长中分母项是 2a，这个 2a 就是那个函数求二阶导数得到的。所以，当前情况下，最好的步长应该是与一次微分成正比，与二次微分成反比的。如下图所示：

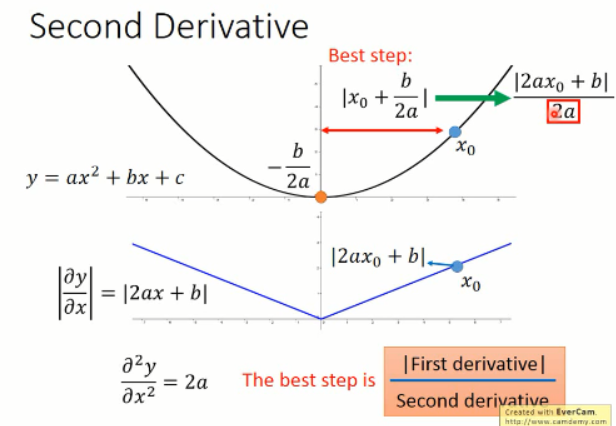
那么，我们再来看看梯度变化的展示图：

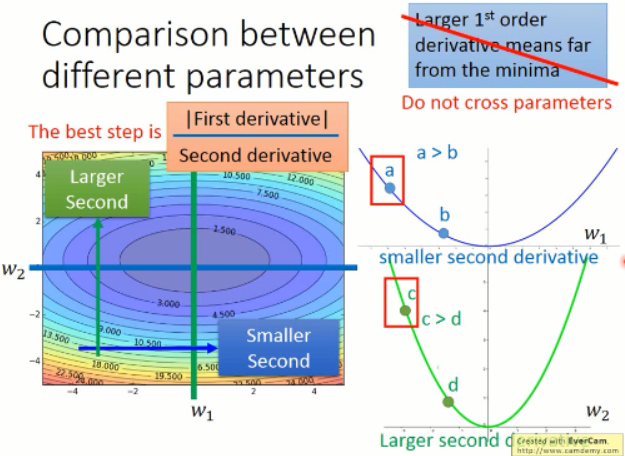
我们可以看到，在 w2 方向上的二阶导数变化是比较小的，而w1方向上的变化是比较大的。我们同时考虑一阶导数和二阶导数，才能真正的反应，某一点，离原点的距离。再来看，a 和 c 点，分子分母都相对的比较小，比较大，就很难看出到底是哪个比较近了。所以，这个时候需要带入，算一算，才知道咯？！！那么，这个现象和 Adagrad 到底有什么关系呢？

神奇的是，Adagrad 就已经在模拟这个比值了：

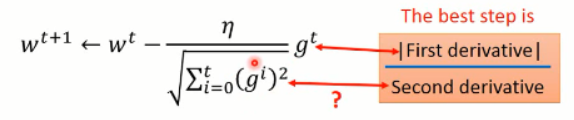
其中的 gt 就是一阶导数，分母虽然不是显示的求解的二阶导数，但是已经是在模拟这个过程了。因为求解二阶导数是需要额外耗费时间的，所以，我们在不增加额外计算量的情况下，可以估计其二阶导数，何乐而不为呢？

假设我们这里有两个函数，其一阶导数分别为：

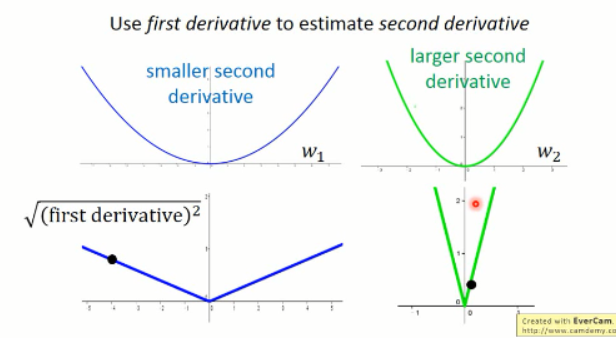
如果我们只采样一个点，我们是很难根据一阶导数估计其二阶导数的，但是我们可以采样很多点啊。。对不对。。。Ok. 如果有很多点，那么：

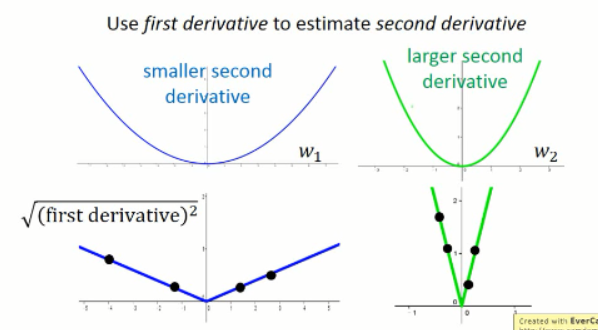
我们有了这么多采样的点，那么，我们可以看出在比较宽的峡谷中，我们得到的梯度是比较小的，而在比较窄的峡谷中，我们得到的梯度是比较大的。我们将这些点都平均起来来看，那么，就可以大致估计出二阶导数的大小了。

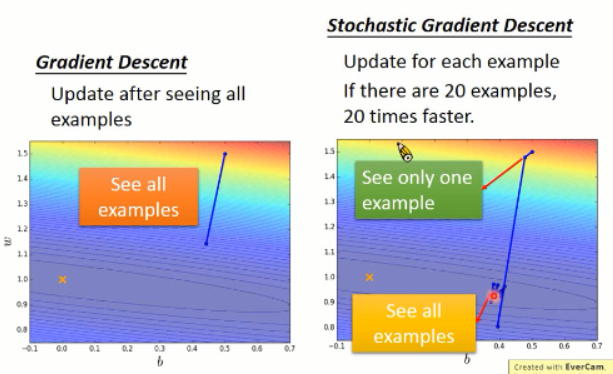
关于 Adagrad 大概就是这样子。接下来 我们来看看什么是随机梯度下降（stochastic gradent descent）：

先说说这个方法的好处吧，恩，就是： make your training faster ...

我们知道，总的 Loss function 是所有样本的 loss 加和，得到的。而梯度下降就是利用所有的 loss 结果来求解。而 SGD 是仅仅对 一个样本进行 loss 的求解，并且更新的时候，只考虑一个样本。也就是说，来一个样本，我就算一次，更新一次，而跟其他的样本没有交集。

接下来就是第三个 tip 了： Feature Scaling

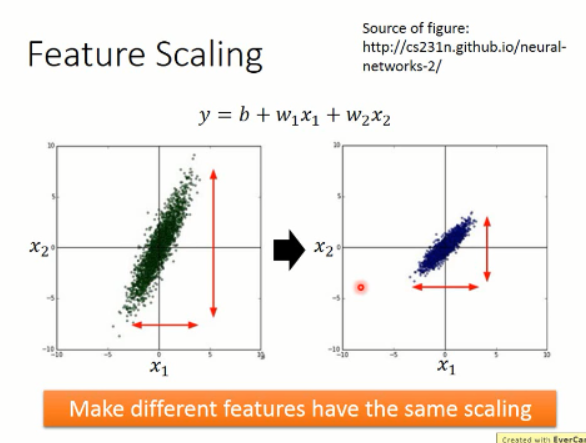
那么，这么做有什么好处呢？加入输入的 feature 中，两个样本 x1 and x2 之间的差距较大，那么，就会导致出现左侧那种椭圆形的等高线的情况，而右侧这种比较一致的 feature 输入，会得到一组比较靠近圆形的等高线。这有什么区别吗？

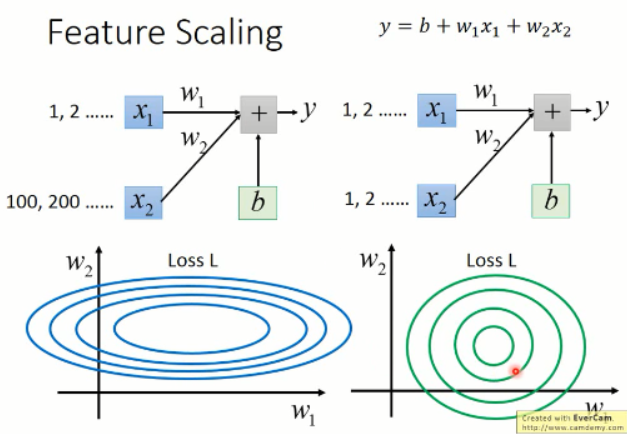
我们继续来看，我们是要用梯度下降来去优化参数，那么我们在左侧椭圆形等高线情况下，就必须得用 Adagrad 这样的优化方法来做了，因为他每一处的梯度都是方向不同的，她是沿着红色曲线的方向进行优化的。

而圆形的这种变化趋势，我们发现，这种可以直接沿着直线的方向，直接就可以优化到圆形的中心点。这实际上是非常平滑的，而且速度上可能有优势。优化起来，比较平滑。

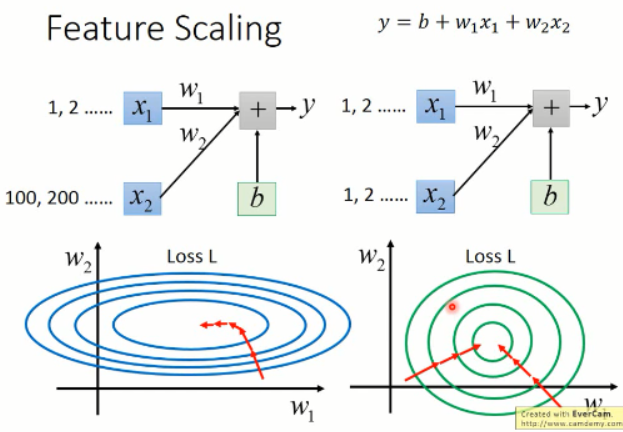
那么，既然有这么多好处，我们该怎么做这个 feature  scaling 呢？

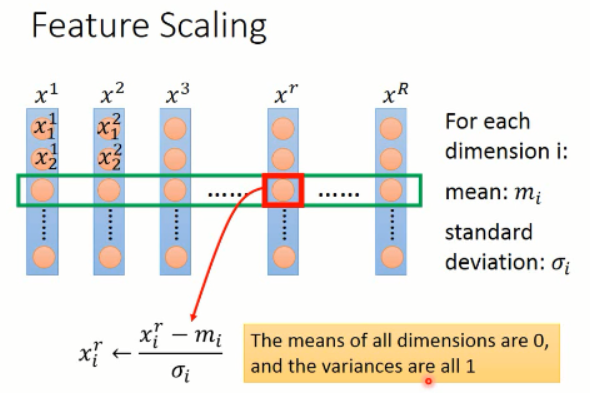
一种比较简单的处理方法就是：对 feature 的每一个维度，我们求出其均值和标准差，然后对每一个 value，减去均值然后再除以标准差，就可以得到修改后的 feature value了。

---

那么，梯度下降方法能work 的原因是什么呢？

我们首先来看一个例子：

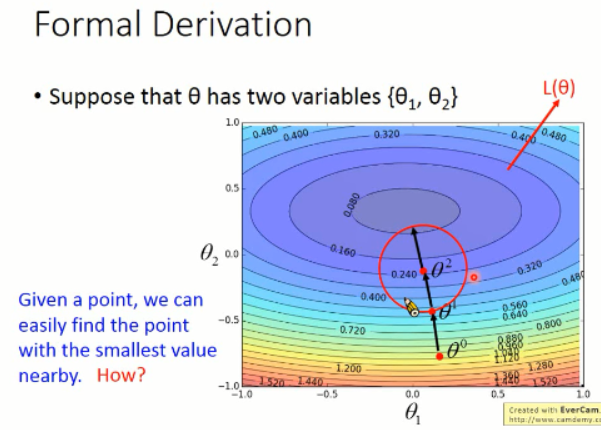
那么，现在我们的问题就是：给定一个点，我们怎么找到其附近区域内的最小的那个点呢？？？我们先来看看泰勒级数的问题：

这里给了一个例子：

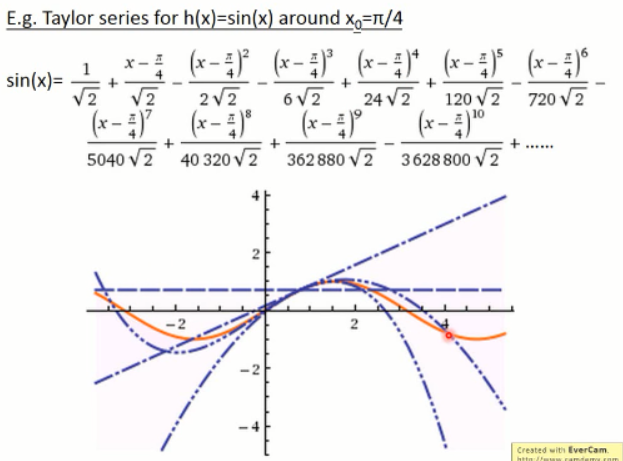
上面提到的是单个变量的泰勒展开式，我们来看看多变量的情况：

那么，我们再次回到那个 formal Derivation 的问题：

我们考虑在圆形内部的情况：

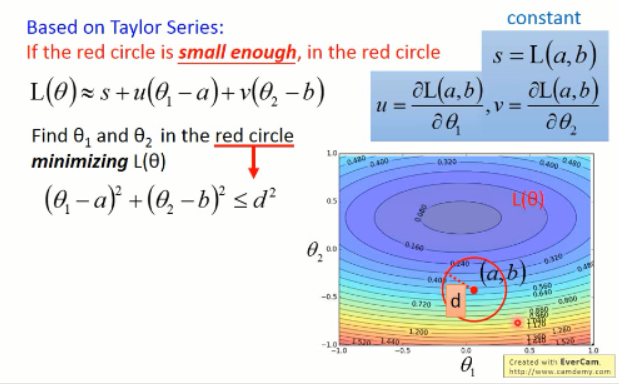
我们所要找的最优的 theta 1 and theta 2 就是和 （u, v）反方向的，并且长度是圆形的半径那样子的。

我们把 u 和 v 带进去之后，就发现，这原来就是 gradient descent：

---

梯度下降的缺点：

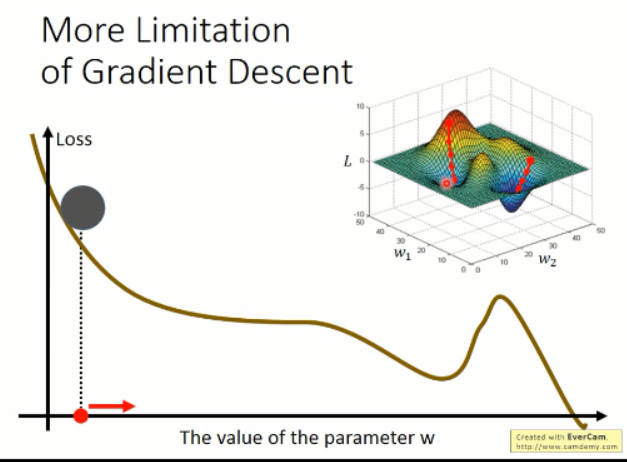
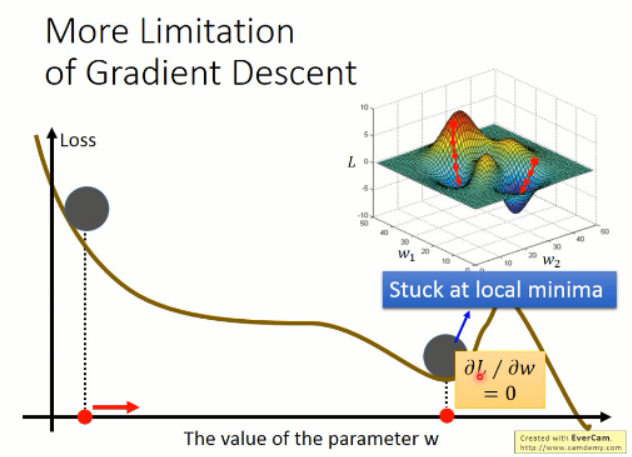
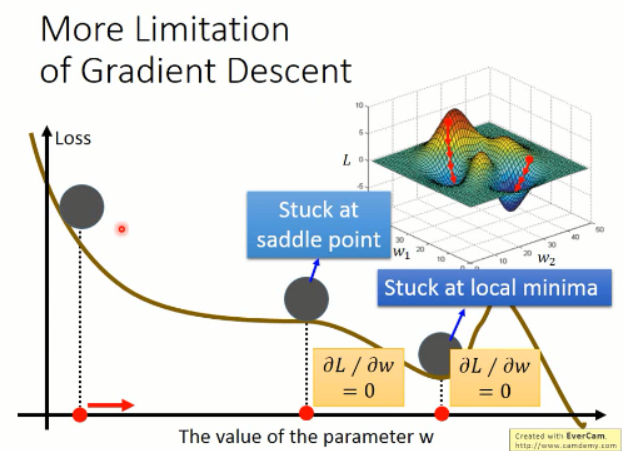
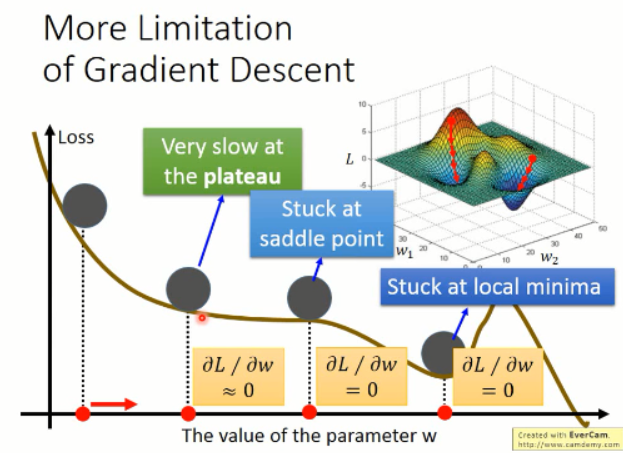
根据以上的图像，我们知道有几个缺点是比较明显的：

1. 容易卡在局部最小值；而不是全局最小；

2. 容易卡在 saddle point；

3. 容易在比较平坦的地方，让你觉得，哦，loss 接近于 0 了，应该训练的差不多了。。。

4. 。。。