HDU 3401 Trade（斜率优化dp）

http://acm.hdu.edu.cn/showproblem.php?pid=3401

题意：
有一个股市，现在有T天让你炒股，在第i天，买进股票的价格为APi，卖出股票的价格为BPi，同时最多买进股票的数量为ASi，卖出股票的数量为BSi。一次交易之后要隔W天之后才能再次交易，并且手上最多持股maxP，问最多可以炒到多少钱。

思路：

首先列一个DP方程：

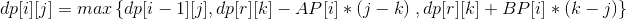
分别代表不买不卖，买进股票，卖出股票三种情况（上面 (j-k)<=AS[i] , (k-j)<=BS[i]）。

那么这里需要枚举r和k的情况，由于相邻两次交易必须隔W天，也就是如果第i天交易了，那么至少要到第i+w+1天才能再次交易。如果我们在第i天要交易股票，那么前w天都是不买不卖的情况，那么前w天的情况都是一样的，所以这以r直接为i-w-1即可。

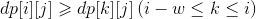
最后是将上面的式子化简一下：

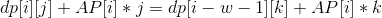
可以看见右边是与k有关的表达式，左边是与j有关的表达式，右边我们只需要选择最大的值即可，那么这就可以用单调队列来优化了。

以买股票为例子说明：

因为是买股票，所以j肯定是大于k的，所以j从小到大枚举。每次计算出右边的值，单调队列保存递减值。每次取队首的最大值，当然队首元素必须满足AS[i]的条件，不满足就出队列。

 #include<cstdio>
 #include<iostream>
 using namespace std;
 const int maxn = +;

 int t, maxp, w, ap[maxn], bp[maxn], as[maxn], bs[maxn], head, tail;
 int dp[maxn][maxn];
 struct node
 {
     int p;
     int x;
 }q[maxn];

 int main()
 {
     //freopen("in.txt","r",stdin);
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d%d",&t,&maxp,&w);
         for(int i=;i<=t;i++)
             scanf("%d%d%d%d",&ap[i],&bp[i],&as[i],&bs[i]);

         for(int i=;i<=t;i++)
             for(int j=;j<=maxp;j++)
                 dp[i][j] = -0x3f3f3f3f;

         for(int i=;i<=w+;i++)
             for(int j=;j<=as[i];j++)
                 dp[i][j] = -j*ap[i];

         for(int i=;i<=t;i++)
         {
             for(int j=;j<=maxp;j++)
                 dp[i][j] = max(dp[i][j],dp[i-][j]);
             if(i<=w+)  continue;
             //买进
             head = tail = ;
             for(int j=;j<=maxp;j++)
             {
                 int x = dp[i-w-][j]+j*ap[i];
                 while(head<tail && q[tail-].x<x)  tail--;
                 q[tail].x = x;
                 q[tail++].p = j;
                 while(head<tail && j-q[head].p>as[i]) head++;
                 dp[i][j] = max(dp[i][j], q[head].x-j*ap[i]);
             }

             //卖出
             head = tail = ;
             for(int j=maxp;j>=;j--)
             {
                 int x = dp[i-w-][j]+j*bp[i];
                 while(head<tail && q[tail-].x<x)  tail--;
                 q[tail].x = x;
                 q[tail++].p = j;
                 while(head<tail && j+bs[i]<q[head].p) head++;
                 dp[i][j] = max(dp[i][j], q[head].x-j*bp[i]);
             }
         }
         int ans = ;
         for(int i=;i<=maxp;i++)
             ans = max(ans,dp[t][i]);
         printf("%d\n",ans);
     }
     return ;
 }