block diagonal matrix 直和 块对角矩阵 不完美 有缺陷 缩放 射影几何

小结：

1、block diagonal matrix  直和 块对角矩阵

A block diagonal matrix is a block matrix that is a square matrix, and having main diagonal blocks square matrices, such that the off-diagonal blocks are zero matrices. A block diagonal matrix A has the form

where A_k is a square matrix; in other words, matrix A is the direct sum of A₁, …, A_n. It can also be indicated as A₁ ⊕ A₂ ⊕ … ⊕ A_n  or  diag(A₁, A₂, …, A_n)  (the latter being the same formalism used for a diagonal matrix). Any square matrix can trivially be considered a block diagonal matrix with only one block.

In linear algebra, a square matrix {\displaystyle A} is called diagonalizable or nondefective if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix {\displaystyle P} such that {\displaystyle P^{-1}AP} is a diagonal matrix. If {\displaystyle V} is a finite-dimensional vector space, then a linear map {\displaystyle T:V\mapsto V} is called diagonalizable if there exists an ordered basis of {\displaystyle V} with respect to which {\displaystyle T} is represented by a diagonal matrix. Diagonalization is the process of finding a corresponding diagonal matrix for a diagonalizable matrix or linear map.^[1] A square matrix that is not diagonalizable is called defective.

Diagonalizable matrices and maps are of interest because diagonal matrices are especially easy to handle; once their eigenvalues and eigenvectors are known, one can raise a diagonal matrix to a power by simply raising the diagonal entries to that same power, and the determinant of a diagonal matrix is simply the product of all diagonal entries. Geometrically, a diagonalizable matrix is an inhomogeneous dilation (or anisotropic scaling) — it scales the space, as does a homogeneous dilation, but by a different factor in each direction, determined by the scale factors on each axis (diagonal entries).

代数角度 幂、行列式  对角元素的处理

几何角度  不同轴的扩缩  不同的方向不同的扩缩因子

同源异型转换

https://en.wikipedia.org/wiki/Homothetic_transformation

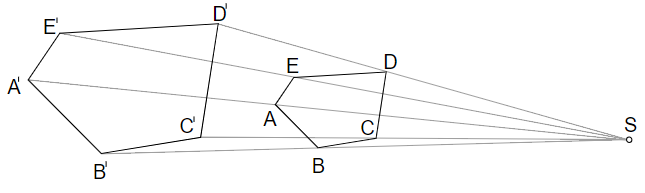
https://en.wikipedia.org/wiki/Scaling_(geometry)

缩放 是 线性变换，是一种相似变换；相似变换多数是非线性的。

Scaling is a linear transformation, and a special case of homothetic transformation. In most cases, the homothetic transformations are non-linear transformations.

Matrix representation

A scaling can be represented by a scaling matrix. To scale an object by a vector v = (v_x, v_y, v_z), each point p = (p_x, p_y, p_z) would need to be multiplied with this scaling matrix:

As shown below, the multiplication will give the expected result:

Such a scaling changes the diameter of an object by a factor between the scale factors, the area by a factor between the smallest and the largest product of two scale factors, and the volume by the product of all three.

The scaling is uniform if and only if the scaling factors are equal (v_x = v_y = v_z). If all except one of the scale factors are equal to 1, we have directional scaling.

In the case where v_x = v_y = v_z = k, scaling increases the area of any surface by a factor of k² and the volume of any solid object by a factor of k³.

isotropic
uniform scaling

各向同性 缩放