SVM数学原理推导&鸢尾花实例

//看了多少遍SVM的数学原理讲解，就是不懂，对偶形式推导也是不懂，看来我真的是不太适合学数学啊，这是面试前最后一次认真的看，并且使用了sklearn包中的SVM来进行实现了一个鸢尾花分类的实例，进行进一步的理解。

1.鸢尾花分类实例

转自：https://www.cnblogs.com/luyaoblog/p/6775342.html

数据集：

特点：每个属性及标记之间使用逗号进行隔开。

#encoding:utf-8
from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib import colors
from sklearn.model_selection import train_test_split
def iris_type(s):
    it = {b'Iris-setosa': 0,
          b'Iris-versicolor': 1,
          b'Iris-virginica': 2}#字符编码的问题
    return it[s]
def show_accuracy(y_hat, y_test, param):
    pass    #空语句，保持结构的完整性。

path = 'C:\\Users\\85937\\Desktop\\sj.txt' # 数据文件路径
data = np.loadtxt(path, dtype=float, delimiter=',', converters={4: iris_type})

x, y = np.split(data, (4,), axis=1)#分割前四列为x,最后一列为y
x = x[:, :2]   #只用了前两列，易于绘图
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1, train_size=0.6) #分割训练集和数据集，训练集是0.6
#clf就是一个超平面了
clf = svm.SVC(C=0.2, kernel='linear', decision_function_shape='ovr')#是分类决策，无论是多少元分类都把它作为二元分类
#clf = svm.SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')#gamma是核函数的参数，一般需要通过交叉验证选择。
#c是惩罚系数，默认是1，一般通过交叉验证来得到，当噪声较大时选较小的。满足一个固定的错误率。
clf.fit(x_train, y_train.ravel())

print (clf.score(x_train, y_train))  #
y_hat = clf.predict(x_train)
show_accuracy(y_hat, y_train, '训练集')
print (clf.score(x_test, y_test))  #在测试集上的精度
y_hat = clf.predict(x_test)
show_accuracy(y_hat, y_test, '测试集')

print ('decision_function:\n', clf.decision_function(x_train))#计算样本点到超平面的函数距离
print ('\npredict:\n', clf.predict(x_train))#对以上的结果进行测试

x1_min, x1_max = x[:, 0].min(), x[:, 0].max()  # 第0列的范围
x2_min, x2_max = x[:, 1].min(), x[:, 1].max()  # 第1列的范围
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]  # 生成网格采样点
grid_test = np.stack((x1.flat, x2.flat), axis=1)  # 测试点

#下面都是进行绘图的操作了。
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])

# print 'grid_test = \n', grid_test
grid_hat = clf.predict(grid_test)       # 预测分类值
grid_hat = grid_hat.reshape(x1.shape)  # 使之与输入的形状相同

alpha = 0.5
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)     # 预测值的显示
# plt.scatter(x[:, 0], x[:, 1], c=y, edgecolors='k', s=50, cmap=cm_dark)  # 样本
plt.plot(x[:, 0], x[:, 1], 'o', alpha=alpha, color='blue', markeredgecolor='k')
plt.scatter(x_test[:, 0], x_test[:, 1], s=120, facecolors='none', zorder=10)  # 圈中测试集样本
plt.xlabel(u'花萼长度', fontsize=13)
plt.ylabel(u'花萼宽度', fontsize=13)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title(u'鸢尾花SVM二特征分类', fontsize=15)
# plt.grid()
plt.show()

//这个真的是超好的一个例子。都不知道该怎么去总结了。

这个就是调用sklearn包去实现，主要的问题在于如何处理这个数据，处理函数过程就直接调用了。

1.首先是numpy的loadtext函数，（路径，数据类型，分隔符，转换）。其中转换是将鸢尾花类型转换为可以处理的。

2.numpy的split函数，（数据，分割的界限，水平方向还是竖直方向）

3.将数据分为训练集和测试集。

4.其中svm的SVC函数，（惩罚系数，核函数，决策函数类型）

其中惩罚系数：是关于分类器的精度，越大分类精度越高，但是会可能出现过拟合

核函数：leaner/rbf(高斯核函数)，当是rbf时，有一个参数gamma，当gamma值越小时分类界面越连续；当gamma值越大时，分类界面越分散，可能会出现过拟合的情况。

重点就是这个决策函数类型了吧，因为当前的数据其实不是一个二分类问题，而是有3中分类结果，那么如何用一个二分类其处理多分类的问题呢？有两种方法如下：

//之后的代码就是验证精度，之后就是画图了，以我现在的水平还看不懂。

2.如何将二分类器作为多分类器呢？

 转自：https://blog.csdn.net/quinn1994/article/details/82662603

 第一：一对一的方法。就是在任意两对样本之间都训练一个二分类器，那么当有一个新样本需要预测的时候，最后得票数最多的类别就是该样本的预测类别。

但是这种方法非常耗费资源，有n个类别的时候，n*(n-1)个分类器。

 第二：一对多的方法。就是为每个类创建一个分类器，最后的预测类别是具有最大SVM间隔的类别。

当一个测试样本输入的时候，这n个分类器都进行预测，最后判定为得分最高的类别。这样相较于上上边是非常节约资源的。

4.其中rbf核函数的参数

还记得Ng的课上说，C相当于正则化项系数1/lamda，当时还不太理解，又看了一下这个博客理解了。

https://blog.csdn.net/ybdesire/article/details/53915093

也就是C愈大，那么模型就越复杂，拟合非线性能力非常强。

C越大，高方差；C越小，高偏差。

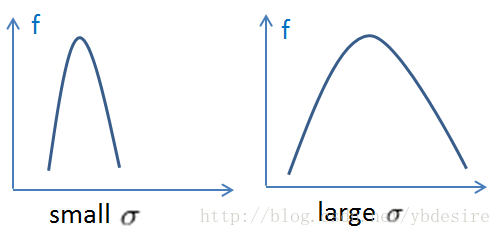
对于rbf中高斯核函数，当σ越大时，曲线越胖，那么对于支持向量附近的样本就作用范围大；

当σ越小时，曲线越瘦，那么只能作用于支持向量样本附近，对于未知样本分类效果差，存在训练准确率高，而测试准确率不高的情况，也就是过拟合的情况。

那么对这一句调用代码：clf = svm.SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')#gamma是核函数的参数，一般需要通过交叉验证选择。

使用了svm中的rbf核函数，其中gamma和高斯函数中的σ有什么关系呢？

转自：https://blog.csdn.net/lujiandong1/article/details/46386201

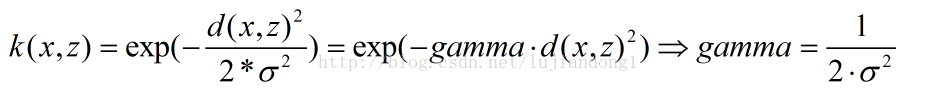
那么在这里看这句调用代码：当C设置的过大的时候，惩罚系数过大，越不能容忍出现误差，会出现曲线过于复杂而过拟合；C越小欠拟合；总之C过大或者过小，都会泛化能力变差。

对于gamma，当gamma过大，也就是σ过小，会出现我们说的过拟合的情况；反之，当gamma过小，σ过大，会出现欠拟合的情况。

那么到底该如何设置参数呢？如何训练参数呢？

转自：https://blog.csdn.net/u011285477/article/details/51900752

使用K折交叉验证，对于数据集，分为K份，每份都作为一次测试集，也就是需要训练K次，得到K个模型，K通常使用10，

最终选取分类准确率最高的一组的参数c和g作为模型参数。

这种思想可以用网格参数寻优来实现，参数C的变化范围，和参数g的变化范围，要在其间找到最优的RBF核参数，

默认步长为1，选出最佳c,g组合。