图 Graph-图的表示及其遍历
2018-03-05 16:19:46
图是计算机科学中的一个非常重要的概念,图是一种多对多的关系。从某种角度上来说树和链表都是图的一种特例。

一、图的抽象数据类型

二、表示图的方法
图是由结点和边构成的,只要能通过某种方式将结点和边的信息表示出来就可以了。以下是两种最常见的图的表示方法,值得一提的是,并不是只有这两种方法来表示图。
- 邻接矩阵
邻接矩阵G[N][N]——N 个顶点从0 到N-1 编号。
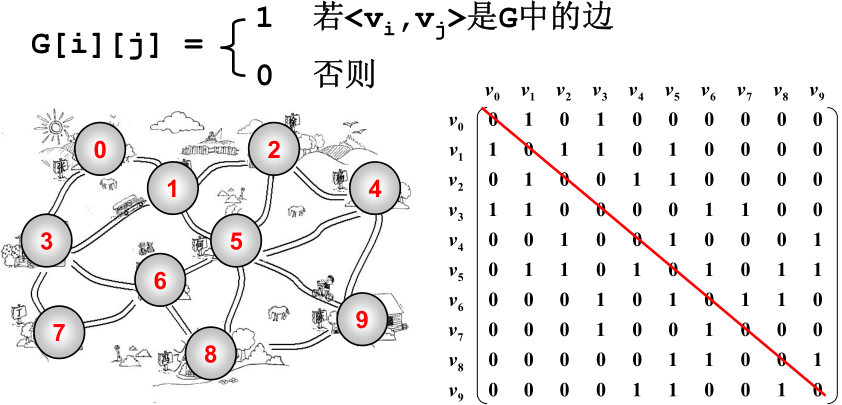
对于无向图,邻接矩阵是对称的,所以可以只保存下三角来减少一半的空间开销。
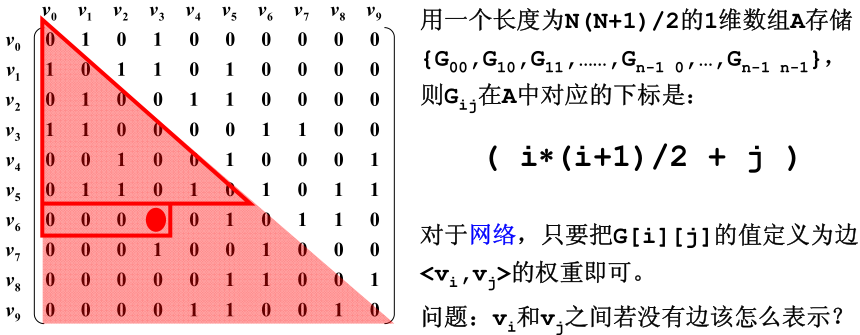
邻接矩阵的优点:
- 直观、简单、好理解
- 方便检查任意一对顶点间是否存在边
- 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
- 方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”)
邻接矩阵的缺点:
- 浪费空间:对于稀疏的图将存放大量无用的数据;
- 浪费时间:比如查找一个结点的邻接点,需要将所有的结点遍历一遍;
- 邻接表
邻接表:G[N]为指针数组,对应矩阵每行一个链表,只存非0元素,也就是直接相邻的结点。一定要足够的稀疏才合算。
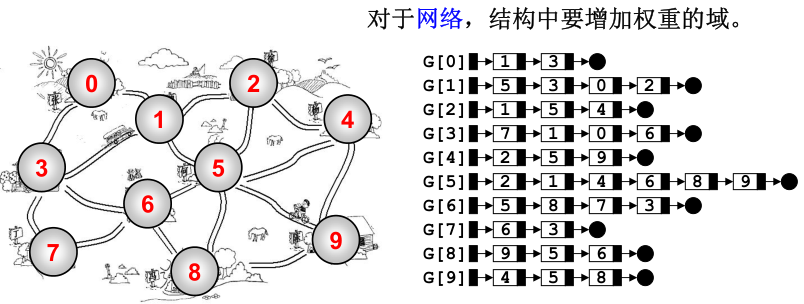
邻接表的特点:
- 方便找任一顶点的所有“邻接点”
- 节约稀疏图的空间(需要N个头指针 + 2E个结点(每个结点至少2 个域))
- 方便计算任一顶点的“度”:仅对于无向图,如果是有向图,那么只能很快的计算出度,入度的计算还是有难度的
- 相对于邻接矩阵,邻接表并不适合很快的查找两个结点之间是否存在边
三、图的遍历
类似于二叉树的遍历,图的遍历也有两种策略,一是深度优先,二是广度优先。
- DFS
所谓遍历,就是将图中所有的结点访问一次,且仅一次。深度优先搜索就是每次到达一个结点,首先申明我访问过他了,避免二次访问,然后在其邻接的结点中挑选是否有还没有被访问的,访问之,重复进行该项操作,即可。
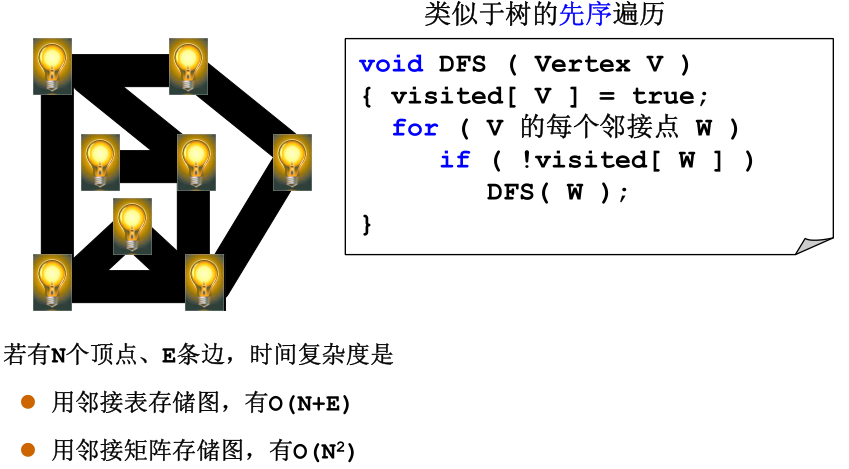
- BFS
BFS类似于二叉树中的层序遍历,使用队列来保存将要访问的结点信息。
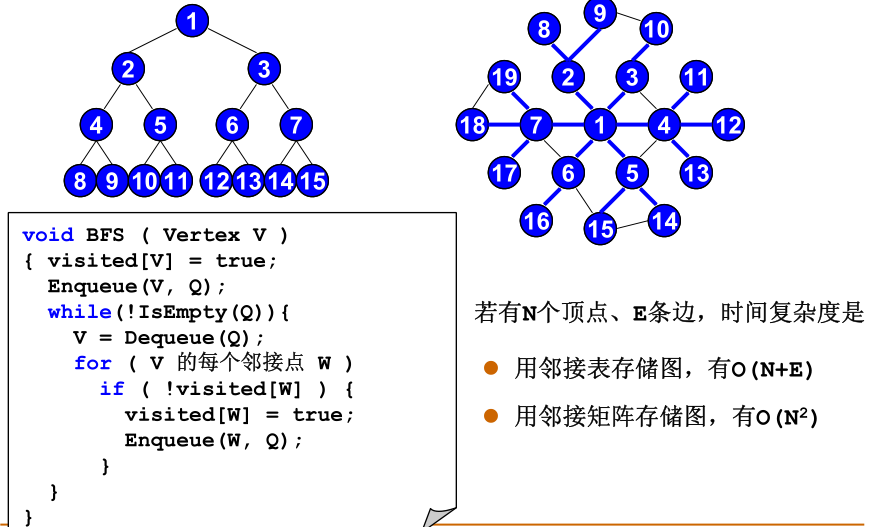
在遍历的过程中,还有一个特别重要的概念--连通性。
连通分量 :无向图的极大连通子图
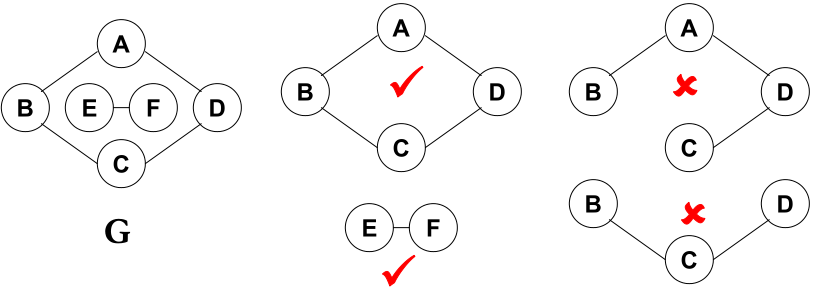
强连通 :有向图中顶点V和W之间存在双向路径,则称V和W是强连通的。
强连通图 :有向图中任意两顶点均强连通
强连通分量 :有向图的极大强连通子图
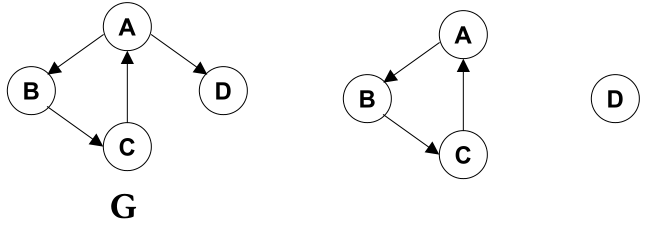
对于不连通的图可以对每个连通分量做一次DFS(或者BFS)。
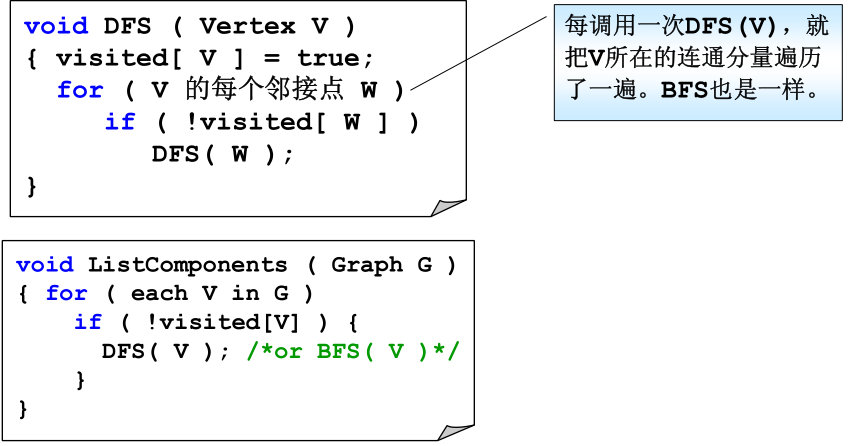
四、应用实例
问题一:解救007
问题描述:詹姆斯邦德被困在孤岛上,孤岛周围环绕的鳄鱼,他的跳跃半径已知,在其跳跃半径内,他可以跳上鳄鱼的头。试问其是否可以上岸。

问题求解:该问题中的结点有孤岛,鳄鱼和岸。请注意,这里岸也是一个结点,所谓的结点其实是一个非常抽象的概念。问题要求的其实就是在这个图中是否可以在遍历过程中遍历到岸这个结点,如果可以那么就返回TRUE。
那是否需要构造一个邻接矩阵,或者邻接表呢?答案是否定的,就像之前提到的,不是说图都要用这两种表示方法来描述,这一题中,可以直接对两个鳄鱼之间的距离进行判断,就可以得到是否存在边的信息。


问题二:六度空间
问题描述:
六度空间理论,你和任何一个陌生人之间所间隔的人不会超过六个。
现给定社交网络图,请对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
问题求解:
按层序遍历,主要的难点就是如何保证只遍历到6层就结束。当然,有种简单的方式就是给每个结点增加一条层数信息,但是这样毫无疑问是非常消耗空间的,这里给出了一种O(1)的解决层数记录的方法,非常巧妙。

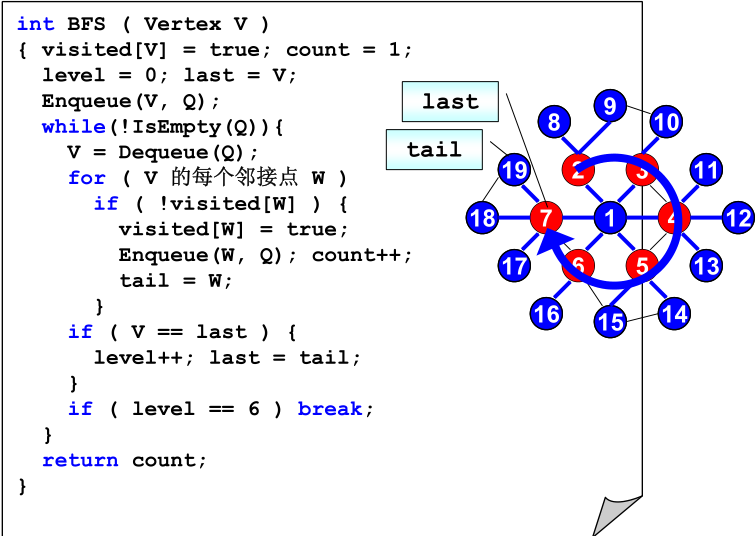
图 Graph-图的表示及其遍历的更多相关文章
- 算法与数据结构基础 - 图(Graph)
图基础 图(Graph)应用广泛,程序中可用邻接表和邻接矩阵表示图.依据不同维度,图可以分为有向图/无向图.有权图/无权图.连通图/非连通图.循环图/非循环图,有向图中的顶点具有入度/出度的概念. 面 ...
- 关于图计算&图学习的基础知识概览:前置知识点学习(Paddle Graph Learning (PGL))
关于图计算&图学习的基础知识概览:前置知识点学习(Paddle Graph Learning (PGL)) 欢迎fork本项目原始链接:关于图计算&图学习的基础知识概览:前置知识点学习 ...
- 纸上谈兵: 图 (graph)
作者:Vamei 出处:http://www.cnblogs.com/vamei 欢迎转载,也请保留这段声明.谢谢! 图(graph)是一种比较松散的数据结构.它有一些节点(vertice),在某些节 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (二)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (三)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 图 Graph
本文主要内容为:图的定义以及基本术语 图的定义 图 图G的组成:由 数据元素的集合E 和 数据间的关系集合E 组成,记作:G = <V, E> 顶点 (vertex):数据元素,V就是顶点 ...
- ADT图及图的实现及图的应用
图: 图中涉及的定义: 有向图: 顶点之间的相关连接具有方向性: 无向图: 顶点之间相关连接没有方向性: 完全图: 若G是无向图,则顶点数n和边数e满足:0<=e<=n(n-1)/2,当e ...
- JanusGraph : 图和图数据库的简介
JanusGraph:图数据库系统简介 图(graph)是<数据结构>课中第一次接触到的一个概念,它是一种用来描述现实世界中个体和个体之间网络关系的数据结构. 为了在计算机中存储图,< ...
- 06. Matplotlib 2 |折线图| 柱状图| 堆叠图| 面积图| 填图| 饼图| 直方图| 散点图| 极坐标| 图箱型图
1.基本图表绘制 plt.plot() 图表类别:线形图.柱状图.密度图,以横纵坐标两个维度为主同时可延展出多种其他图表样式 plt.plot(kind='line', ax=None, figsiz ...
随机推荐
- puma 配置,启动脚本
版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/menxu_work/article/details/24547923 配置: puma_server ...
- iOS开发- 速学Swift-中文概述
Swift是什么? Swift是苹果于WWDC 2014公布的编程语言,这里引用The Swift Programming Language的原话: Swift is a new programmin ...
- 011-HQL中级1-Hive快捷查询:不启用Mapreduce job启用Fetch task三种方式介绍
如果你想查询某个表的某一列,Hive默认是会启用MapReduce Job来完成这个任务,如下: hive; Total MapReduce jobs Launching Job out since ...
- sails route(1) -用户定义路由
sails支持两种类型的路由: custom(or "explicit") andautomatic(or "implicit"). 先来看一下custom 即 ...
- 如何制作一款HTML5 RPG游戏引擎——第一篇,地图类的实现
一,话说天下大事 前不久看到lufy的博客上,有一位朋友想要一个RPG游戏引擎,出于兴趣准备动手做一做.由于我研究lufylegend有一段时间了,对它有一定的依赖性,因此就准备将这个引擎基于lufy ...
- Apache配置虚拟主机的三种方法(基于IP、端口、域名)
1 Apache虚拟主机的实现方式有3种. 基于IP的虚拟主机 基于端口的虚拟主机 基于域名的虚拟主机 2.1 启用虚拟主机的准备工作 2.1.1安装httpd [root@mail httpd]# ...
- glib简单记录包括字符串,主循环,回调函数和xml解析
一.将最近用到的glib字符串功能整理了下直接用程序记录比较好看懂 #define MAX_LEN 100gchar * demo (char* msg, ...){ gchar * pcfgf ...
- 查看Oracle latch _spin_count默认值
查看Oracle latch _spin_count默认值 SELECT X.KSPPINM NAME, Y.KSPFTCTXVL VALUE, Y.KSPFTCTXDF ISDEFAULT FRO ...
- Mediakit报告设备商的空间不足以执行此操作的纯MAC解法
使用Mac对磁盘进行分区,显示“Mediakit报告设备商的空间不足以执行此操作”,该怎么办? What 买了一个4TB的移动硬盘,准备进行分区给Time Machine用. 硬盘自带是HDFS的,所 ...
- [golang note] 类型系统
值和引用 • 值语义和引用语义 值语义和引用语义的差别在于赋值: b = a b.Modify() 如果b的修改不会影响a的值,那么属于值类型,否则属于引用类型. • 值类型和引用类型 √ 引用类型一 ...
