【交叉染色法判断二分图】Claw Decomposition UVA - 11396

题目链接：https://cn.vjudge.net/contest/209473#problem/C

先谈一下二分图相关：

一个图是二分图的充分必要条件：
该图对应无向图的所有回路必定是偶环（构成该环形的边的数量为偶数）。
暂时不证明，后证。

那么怎么判断一个图的回路是奇环还是偶环呢？

交叉染色法。

随机选择一个点，染成红色，把所有跟它相邻的点染成绿色，再由被染色的绿点出发，把相邻的点染成红色……

即对于一个点和他相邻的点（两个点之间有边相连叫做相邻），颜色必定不同，如果相同，那么是奇环。

例如1（红）--2（绿）--3（红）--4（绿）--5（红），颜色是跳跃性相同的，如果是奇环那么一定会出现相邻两点颜色相同的情况。

下面放代码：

bool _dfs(int u){

    int v;
    for(int i=;i<g[u].size();i++){
        v=g[u][i];
        if(color[v]==color[u])return false;
        else if(!color[v]){
            color[v]=color[u]^;
            if(!_dfs(v))return false;
        }
    }
    return true;
}

回归题目。

题目大意：给出一个图，这个图上的每个点的度数都为3，判断这个图可不可以拆分成“爪”字形。也就是所有的边都要用上，并且只用一次，点可以无限使用（至少使用一次），把原图拆分成全为

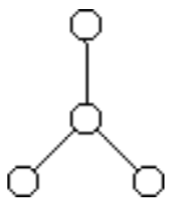这种样子的子图。（注意是打散之后！只有这一个样子没有其他连边了！！！）

解题思路：

借助了一下别人的智慧orz。对于题目进行分析，我们能够发现每个点只有两种用法：1、一个“爪”的中心点。2、一个“爪”的旁支。两个条件绝对不可能同时满足，（证明：如果该点满足1，那么从这个点出发的三条边就是延伸边，不可能作为辅助边。如果该点满足2，那么从这个点出发的至少有一条边是辅助边，那么剩下的少于三条边不足以支撑这个点变为爪中心。）

有了这个前提，我们就能很容易地想到二分图两个集合的互斥，那么对于每个点，在和他相连的另一个点上连边，判断一下是否构成二分图就可以了。

（为什么能构成二分图就有解？一个点如果被规定为爪中心，那么它在跟它相连的三个点全为旁支的情况下，是一定能成立的。【关键在于度数全为3】；一个点如果被规定为旁支，那么跟它相连的所有点都必定是爪中心，所以它的三条边也能分配完毕。）

坑点：

图可能不连通。

下面放上0msAC代码：

 #include<stdio.h>
 #include<string.h>
 #define MAXN 305

 int n,g[MAXN][MAXN],color[MAXN];

 bool _dfs(int p,int t){

     int i;
     color[p]=t;
     for(i=;i<=n;i++)
         if(g[p][i]){
             if(color[i]==t)return false;
             if(!color[i])
                 if(!_dfs(i,t^))return false;

         }
     return true;
 }

 int main(){

     int x,y,i;
     while(true){
         scanf("%d",&n);
         if(!n)break;
         memset(g,,sizeof(g));
         memset(color,,sizeof(color));
         while(true){
             scanf("%d%d",&x,&y);
             if(x+y==)break;
             g[x][y]=g[y][x]=true;
         }
         for(i=;i<=n;i++)
             if(!color[i])
                 if(!_dfs(i,))break;
         if(i>n)puts("YES");
         else puts("NO");
     }
     return ;
 }