2017北京国庆刷题Day3 morning

期望得分：100+60+0=160

实际得分：100+30+0=130

考场上用的哈希

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define mod 1000003
#define mod2 100003
char s[];
bool vis[mod],vis2[mod2];
int hash1,hash2;
int gethash()
{
    int len=strlen(s);
    sort(s,s+len);
    hash1=s[]-'A'+,hash2=hash1;
    for(int i=;i<len;i++)
    {
        hash1=(hash1*+(s[i]-'A')+)%mod;
        hash2=(hash2*+(s[i]-'A')+)%mod2;
    }
}
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    int n,ans=;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%s",s);
        gethash();
        if(!vis[hash1] || !vis2[hash2]) vis[hash1]=true,vis2[hash2]=true,ans++;
    }
    printf("%d",ans);
}

myself

std直接sort，map 判重结构体

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<map>

using namespace std;

struct node
{
       int z[];
       node()
       {
             memset(z,,sizeof(z));
       }
       bool operator<(const node &a)const
       {
            for (int b=;b<=;b++)
            if (z[b]!=a.z[b]) return z[b]<a.z[b];
            return false;
       }
}now;

map<node,bool> use;

int ans,n;

char s[];

int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    scanf("%d",&n);
    for (int a=;a<=n;a++)
    {
        scanf("%s",s+);
        int l=strlen(s+);
        memset(now.z,,sizeof(now.z));
        for (int a=;a<=l;a++)
            now.z[s[a]-'A'+]++;
        if (!use[now]) use[now]=true,ans++;
    }
    printf("%d\n",ans);

    return ;
}

std

设分成的每段长为Li，g=gcd（Li）

那么一共有n/g 个单位

设f[g]表示以g为周长，且三边gcd为1 的三角形的个数

设h[n/g]表示把n/g个单位 分配给任意多个三角形的个数

那么 ans=Σ f[g]*h[n/g]   （g|n）

求f[g]：

设g=a+b+c，且a<=b<=c

对b和c的大小分两种情况讨论：

① b==c ：

==> g=a+2b，那么b∈[ceil(g/3),floor((g-1)/2)]

所以f[g]=floor((g-1)/2）- ceil(g/3) +1

② b<c ：

a，b，c 的每一种方案都可以看做由 a，b，c-1的每一种方案转移过来

但有一种除外：a+b=c，因为此时a，b，c-1 合法，a，b，c 不合法

当g为偶数时，a+b+a+b=g，g=2*（a+b），所以有floor（g/4）个

所以f[g]=f[g-1]+ （b&1）？ 0 ： -g/4

然后因为要求三边长互质，所以枚举g的每个因数k，f[g]-=f[k]

求h[i]：

把i个物品分成任意份的方案数=C（i-1,0）+C（i-1，1）+……+C（i-1，i-1）

= 2^(i-1)

#include<cmath>
#include<cstdio>
#include<algorithm>

#define N 1000001
const int mod=1e9+;

using namespace std;

int f[N],g[N];
int divisor[N],cnt;

void ADD(int &a,int b) { a+=b; a>=mod ? a-=mod : ; }

int main()
{
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    int n; scanf("%d",&n);
    for(int a=;a<=n;a++)
    {
        f[a]=f[a-]; ADD(f[a],(a->>)-ceil(a*1.0/)+);
        ADD(f[a],(a&) ?  : -a/);
    }
    for(int a=;a*a<=n;++a)
        if(n%a==)
        {
            divisor[++cnt]=a;
            if(a*a!=n) divisor[++cnt]=n/a;
        }
    sort(divisor+,divisor+cnt+);
    for(int i=;i<=cnt;i++)
        for(int j=;j<i;j++)
            if(divisor[i]%divisor[j]==) ADD(f[divisor[i]],mod-f[divisor[j]]);
    g[]=;
    for(int i=;i<=n;i++) g[i]=g[i-],ADD(g[i],g[i-]);
    int ans=;
    for(int i=;i<=cnt;i++) ADD(ans,1ll*f[divisor[i]]*g[n/divisor[i]-]%mod);
    printf("%d",ans);
}

考场上WW的组合数，得了30，挂了30

#include<cstdio>
using namespace std;
int n;
int one[];
int C[][];
const int mod=1e9+;
bool check(int i,int j,int k)
{
    if(!i || !j || !k) return false;
    if(!((i<=j)&&(j<=k))) return false;
    if(i+j<=k) return false;
    if(j-i>=k) return false;
    return true;
}
void pre()
{
    for(int i=;i<=n;i++)
        for(int j=;j<=i;j++)
            for(int k=j;k<=i;k++)
                if(check(j,i-j-k,k)) one[i]++;
    for(int i=;i<=n;i++) C[i][]=;
    for(int i=;i<=n;i++) C[][i]=;
    for(int i=;i<=n;i++)
        for(int j=;j<=i;j++)
            C[i][j]+=C[i-][j-]+C[i-][j],C[i][j]%=mod;
    int tot,ans=;
    for(int i=;i<=n;i++)
        if(n%i==)
        {
            tot=n/i;
            tot--;
            if(!tot) { ans+=one[i]; continue;}
             for(int j=;j<=tot;j++) 

              ans=(ans+1ll*one[i]*C[tot][j-]*j)%mod;

        }
    printf("%d",ans);
}
int main()
{
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    scanf("%d",&n);
    pre();
}

这题竟然是个容斥原理

解决本题的关键：行交换、列交换对答案不影响

将左视图按从下往上递减，正视图从左往右递减排列

那整张图的高度从左下到右上呈阶梯状递减

这样所有高度相同的呈现倒‘L’形，如下图所示蓝色部分

如果我们按高度递减的顺序依次计算每个倒‘L’形的方案数，那么这些倒‘L’形相对独立

答案就是所有倒‘L’形答案的乘积

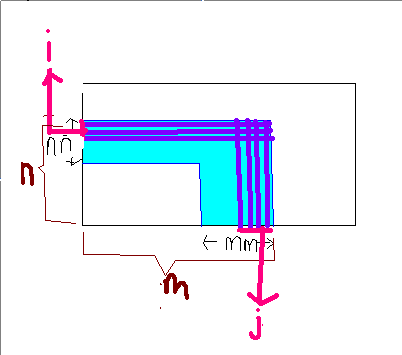
如何计算单个倒‘L’形的答案？——容斥原理

假设上图为已经按高度排好序的图

设当前正在处理高度为h的倒‘L’形

令nn表示当前有nn行的左视图高度为h，mm表示当前有mm列的主视图高度为h

n表示当前有n行的左视图高度>=h，m表示当前有m列的主视图高度>=h

定义性质pk表示 在这nn行mm列中，有k行/列不满足看到的高度为h

那根据容斥原理，

不具有任何一个性质p的方案和=

全集-Σ|pi|+Σ|pi∩pj|-Σ|pi∩pj∩pk|+…+（-1）^m*|p1∩p2∩…∩pm|

也就是所有方案-所有1行/列不满足条件的方案+所有2行/列不满足条件的方案-……

如何求有k行/列不满足条件的方案数？

设现在要求在倒‘L’形中，有i行j列不满足条件的方案数A，i+j=k

那么A分为两部分

① i行j列不能满足条件的部分：

当前高度为h，不能满足条件，每一个各自可以填[0,h-1],每个格子有h种方案

所以此时方案数=h^ （n*m-(n-i)*(m-j)）

② 倒‘L’形中其他位置可以任意填的部分

当前高度为h，任意填就是可以填[0,h]，每个各自有h+1种方案

所以此时的方案数=（h+1）^（(n-i)*(m-j)-(n-nn)*(m-mm)）

这是选定i行j列，所以还要乘上在nn行中选i行，在mm列中选j列的方案

终上所述，每个倒‘L’形 的答案为 （-1）^（i+j）* C（nn，i）* C（mm，j）* h^ （n*m-(n-i)*(m-j)） * （h+1）^（(n-i)*(m-j)-(n-nn)*(m-mm)）

#include<cstdio>
#include<algorithm>

using namespace std;

typedef long long LL;

#define N 51
#define H 10001
const int mod=1e9+;

int a[H],b[H];
int n,m;
int C[N][N];

void pre(int k)
{
    for(int i=;i<=k;i++) C[i][]=;
    for(int i=;i<=k;i++)
        for(int j=;j<=i;j++)
            C[i][j]=(C[i-][j]+C[i-][j-])%mod;
}

int pow(int a,int b)
{
    int res=;
    for(;b;b>>=,a=1ll*a*a%mod)
        if(b&) res=1ll*res*a%mod;
    return res;
}

int cal(int n,int m,int nn,int mm,int h)
{
    int res=,tmp;
    for(int i=;i<=nn;++i)
        for(int j=;j<=mm;++j)
        {
            tmp=1ll*pow(h,n*m-(n-i)*(m-j))*pow(h+,(n-i)*(m-j)-(n-nn)*(m-mm))%mod*C[nn][i]%mod*C[mm][j]%mod;
            if((i+j)&) res=((res-tmp)%mod+mod)%mod;
            else res+=tmp,res%=mod;
        }
    return res;
}

int main()
{
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    int x;
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;++i) scanf("%d",&x),a[x]++;
    for(int i=;i<=m;++i) scanf("%d",&x),b[x]++;
    pre(max(n,m));
    LL res=;
    int nown=,nowm=;
    for(int i=;i>=;i--)
        if(a[i] || b[i])
        {
            nown+=a[i]; nowm+=b[i];
            res=1ll*res*cal(nown,nowm,a[i],b[i],i)%mod;
        }
    printf("%I64d",res);
}