NOIP 2014 提高组 Day1

期望得分：100+100+50=250

实际得分：100+100+50=250

此次NOIP ZJ省一分数线：500，SD：345

https://www.luogu.org/problem/lists?name=&orderitem=pid&tag=83%7C31

T1 生活大爆炸版石头剪刀布

题目描述

石头剪刀布是常见的猜拳游戏：石头胜剪刀，剪刀胜布，布胜石头。如果两个人出拳一样，则不分胜负。在《生活大爆炸》第二季第8 集中出现了一种石头剪刀布的升级版游戏。

升级版游戏在传统的石头剪刀布游戏的基础上，增加了两个新手势：

斯波克：《星际迷航》主角之一。

蜥蜴人：《星际迷航》中的反面角色。

这五种手势的胜负关系如表一所示，表中列出的是甲对乙的游戏结果。

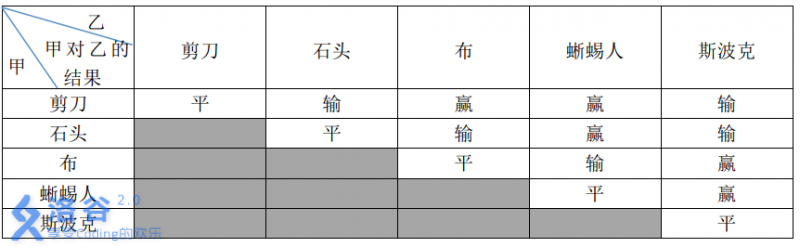
现在，小A 和小B 尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的，但周期长度不一定相等。例如：如果小 A以“石头 - 布- 石头- 剪刀- 蜥蜴人- 斯波克”长度为6 的周期出拳，那么他的出拳序列就是“石头- 布- 石头- 剪刀- 蜥蜴人- 斯波克- 石头- 布- 石头- 剪刀- 蜥蜴人- 斯波克- ……”，而如果小B 以“剪刀- 石头- 布- 斯波克- 蜥蜴人”长度为5 的周期出拳，那么他出拳的序列就是“剪刀- 石头- 布- 斯波克- 蜥蜴人- 剪刀- 石头- 布-斯波克- 蜥蜴人- ……”

已知小A 和小B 一共进行N 次猜拳。每一次赢的人得1 分，输的得0 分；平局两人都得0 分。现请你统计N 次猜拳结束之后两人的得分。

输入输出格式

输入格式：

输入文件名为rps.in。

第一行包含三个整数：N ，NA，NB，分别表示共进行 N 次猜拳、小 A 出拳的周期长度，小B 出拳的周期长度。数与数之间以一个空格分隔。

第二行包含NA个整数，表示小 A 出拳的规律，第三行包含NB个整数，表示小 B 出拳的规律。其中，0 表示“剪刀”，1 表示“石头”，2 表示“布”，3 表示“蜥蜴人”， 4 表示“斯波克”。数与数之间以一个空格分隔。

输出格式：

输出文件名为rps.out 。

输出一行，包含两个整数，以一个空格分隔，分别表示小A 、小B 的得分。

输入输出样例

输入样例#1：

10 5 6

0 1 2 3 4

0 3 4 2 1 0

输出样例#1：

6 2

输入样例#2：

输出样例#2：

4 4

说明

对于100%的数据，0 < N ≤ 200 ，0 < NA ≤ 200 ， 0 < NB ≤ 200 。

不打表都对不起给出的表格

#include<cstdio>

using namespace std;

int c[][]={{,,,,},{,,,,},{,,,,},{,,,,},{,,,,}};

int n,na,nb,a[],b[];

int main()

{

    freopen("rps.in","r",stdin);

    freopen("rps.out","w",stdout);

    scanf("%d%d%d",&n,&na,&nb);

    for(int i=;i<=na;i++) scanf("%d",&a[i]);

    for(int i=;i<=nb;i++) scanf("%d",&b[i]);

    int i=,j=,sa=,sb=;

    for(int k=;k<=n;k++)

    {

        if(i>na) i=;

        if(j>nb) j=;

        if(c[a[i]][b[j]]) sa++;

        else if(c[b[j]][a[i]]) sb++;

        i++;j++;

    }

    printf("%d %d",sa,sb);

}

T2 联合权值

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007 取余。

输入输出样例

输入样例#1：

输出样例#1：

20 74

说明

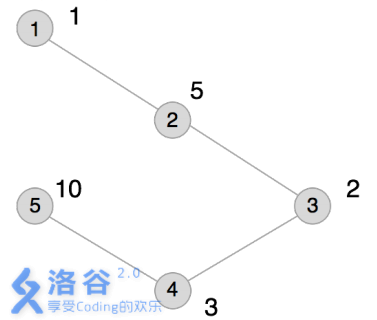
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

第一反应：对于60%的数据

枚举每个节点，dfs 距离为2的点，一个一个算

AC做法：

设sum[i]表示与点i直接相连的点权和

可以发现，对于每个点i，它对联值权值之和的贡献=w[i]*sum[j] （j是与i直接相连的点）

令maxn[i]表示与i直接相连的点中，最大的点权和

那么对于i，最大的联合权值=w[i]*max（maxn[j]）（j是与i直接相连的点）

注意我们在计算最大的联合权值时，maxn[j]可能就是点i的权值，不合法

所以同时记录maxn[j]是哪个点的点权，同时记录一个次大点权maxn_[j]

统计答案时，枚举点i，枚举与i直接相连的点j，若maxn[j]对应得点=i，用次大点权来算

AC代码：

#include<cstdio>

#include<algorithm>

#define N 200001

#define mod 10007

using namespace std;

int n,maxn[N],sum[N],maxn_[N],wh[N];

int ans1,ans2;

int front[N],to[N*],next[N*],tot,w[N];

void add(int u,int v)

{

    to[++tot]=v; next[tot]=front[u]; front[u]=tot;

}

int main()

{

    freopen("linkb.in","r",stdin);

    freopen("linkb.out","w",stdout);

    scanf("%d",&n);

    int u,v;

    for(int i=;i<n;i++)

    {

        scanf("%d%d",&u,&v);

        add(u,v);

        add(v,u);

    }

    for(int i=;i<=n;i++) scanf("%d",&w[i]);

    for(int i=;i<=n;i++)

     for(int j=front[i];j;j=next[j])

      {

           sum[i]=(sum[i]+w[to[j]])%mod;

           if(w[to[j]]>=maxn[i])

           {

               maxn_[i]=maxn[i];

            maxn[i]=w[to[j]];

               wh[i]=to[j];

         }

         else if(w[to[j]]>maxn_[i])

            maxn_[i]=w[to[j]];

      }

    for(int i=;i<=n;i++)

     for(int j=front[i];j;j=next[j])

      {

           if(wh[to[j]]==i) ans1=max(ans1,w[i]*maxn_[to[j]]);

           else    ans1=max(ans1,w[i]*maxn[to[j]]);

         ans2=(ans2+w[i]*(sum[to[j]]-w[i]+mod))%mod;

      }

    printf("%d %d",ans1,ans2);

}

60%代码：

#include<cstdio>

#include<algorithm>

#define N 200001

using namespace std;

int n,w[N],front[N],to[N*],nextt[N*],tot;

int ans1,ans2,k;

bool v[N];

const int mod=;

void dfs(int now,int sum)

{

    v[now]=true;

    if(sum==)

    {

        ans1=max(ans1,w[now]*w[k]);

        ans2=(ans2+w[now]*w[k])%mod;

        return ;

    }

    for(int i=front[now];i;i=nextt[i])

     if(!v[to[i]])

      {

           dfs(to[i],sum+);

           v[to[i]]=false;

      }

}

void add(int u,int v)

{

    to[++tot]=v; nextt[tot]=front[u]; front[u]=tot;

}

int main()

{

        freopen("linkb.in","r",stdin);

    freopen("linkb.out","w",stdout);

    scanf("%d",&n);

    int u,h;

    for(int i=;i<n;i++)

    {

        scanf("%d%d",&u,&h);

        add(u,h);

        add(h,u);

    }

    for (int i=;i<=n;i++) scanf("%d",&w[i]);

    for(int i=;i<=n;i++)

     {

         dfs(k=i,);

         v[i]=false;

     }

    printf("%d %d",ans1,ans2);

}

T3 飞扬的小鸟

题目描述

Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编：

游戏界面是一个长为n ，高为 m 的二维平面，其中有k 个管道（忽略管道的宽度）。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。
小鸟每个单位时间沿横坐标方向右移的距离为1 ，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度X ，每个单位时间可以点击多次，效果叠加；

如果不点击屏幕，小鸟就会下降一定高度Y 。小鸟位于横坐标方向不同位置时，上升的高度X 和下降的高度Y 可能互不相同。

小鸟高度等于0 或者小鸟碰到管道时，游戏失败。小鸟高度为 m 时，无法再上升。

现在，请你判断是否可以完成游戏。如果可以，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

输入输出格式

输入格式：

输入文件名为 bird.in 。

第1 行有3 个整数n ，m ，k ，分别表示游戏界面的长度，高度和水管的数量，每两个整数之间用一个空格隔开；

接下来的n 行，每行2 个用一个空格隔开的整数X 和Y ，依次表示在横坐标位置0 ~n- 1上玩家点击屏幕后，小鸟在下一位置上升的高度X ，以及在这个位置上玩家不点击屏幕时，小鸟在下一位置下降的高度Y 。

接下来k 行，每行3 个整数P ，L ，H ，每两个整数之间用一个空格隔开。每行表示一个管道，其中P 表示管道的横坐标，L 表示此管道缝隙的下边沿高度为L ，H 表示管道缝隙上边沿的高度（输入数据保证P 各不相同，但不保证按照大小顺序给出）。

输出格式：

输出文件名为bird.out 。

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出1 ，否则输出0 。

第二行，包含一个整数，如果第一行为1 ，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

输入输出样例

输入样例#1：

输出样例#1：

1

6

输入样例#2：

输出样例#2：

0

3

说明

【输入输出样例说明】

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

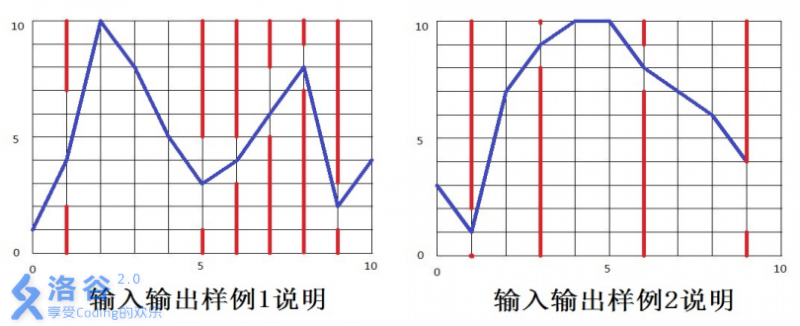
【数据范围】

对于30% 的数据：5 ≤ n ≤ 10，5 ≤ m ≤ 10，k = 0 ，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于50% 的数据：5 ≤ n ≤ 2 0 ，5 ≤ m ≤ 10，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于70% 的数据：5 ≤ n ≤ 1000，5 ≤ m ≤ 1 0 0 ；

对于100%的数据：5 ≤ n ≤ 100 0 0 ，5 ≤ m ≤ 1 0 00，0 ≤ k < n ，0<X < m ，0<Y <m，0<P <n，0 ≤ L < H ≤ m ，L +1< H 。

50分做法：暴力dfs

70分做法：

向上的是完全背包，向下的是01背包

令f[i][j]表示到达横坐标为i，高度为j的最小点击数

向上的状态转移方程：f[i][j]=min( f[i-1][j-up[i-1]*k]+k ) k<=m/up[i-1]

向下的状态转移方程：f[i][j]=min( f[i-1][j+down[i-1]])

时间复杂度：O（nm²）

100分做法：

在向上的状态转移方程中，

若p=j-up[i-1]*k，那么到达状态p 和到达状态j 的很多起点是重复的

也就是说，由重复的相同状态转移到了不同状态

优化这个重复的相同状态

假设一次上升高度x

f[i][j-x]= min（ f[i-1][ (j-x)-x*(k-1) ]+k-1 ）

原式:f[i][j]= min（ f[i-1][j-x*k]+k）

发现当k>1时，f[i][j]=f[i][j-x]+1

所以新的向上的状态转移方程：f[i][j]=min（f[i-1][j-x],f[i][j-x]）+1

AC代码：

#include<cstdio>

#include<algorithm>

#define N 10001

#define inf 20001

using namespace std;

int n,m,k,ok;

int up[N],down[N],top[N],bot[N];

int f[N][];

bool have[N];

int main()

{

    freopen("birda.in","r",stdin);

    freopen("birda.out","w",stdout);

    scanf("%d%d%d",&n,&m,&k);

    int x;

    for(int i=;i<n;i++) scanf("%d%d",&up[i],&down[i]);

    for(int i=;i<=k;i++)

    {

        scanf("%d",&x);have[x]=true;

        scanf("%d%d",&bot[x],&top[x]);

    }

    for(int i=;i<=n;i++)

     if(!top[i]) top[i]=m+;

    for(int i=;i<=n;i++)

     for(int j=;j<=m;j++)

      f[i][j]=inf;

    for(int i=;i<=m;i++) f[][i]=;

    for(int i=;i<=bot[];i++) f[][i]=inf;

    for(int i=top[];i<=m;i++) f[][i]=inf;

    for(int i=;i<=n;i++)

     {

         for(int j=up[i-]+;j<=m;j++) f[i][j]=min(f[i-][j-up[i-]],f[i][j-up[i-]])+;

         for(int j=m-up[i-];j<=m;j++) f[i][m]=min(f[i][m],min(f[i][j],f[i-][j])+);

         for(int j=;j<=m-down[i-];j++) f[i][j]=min(f[i][j],f[i-][j+down[i-]]);

         for(int j=;j<=bot[i];j++) f[i][j]=inf;

         for(int j=top[i];j<=m;j++) f[i][j]=inf;

         if(!have[i]) continue;

         int j;

         for(j=bot[i]+;j<=top[i];j++)

          if(f[i][j]<inf) {ok++;break;}

         if(j>top[i]) {printf("0\n%d",ok); return ;}

     }

     int sum=inf;

     for(int i=;i<=m;i++) sum=min(sum,f[n][i]);

     printf("1\n%d",sum);

}

一点儿小错误：

int j;
for(j=bot[i]+1;j<=top[i];j++) if(f[i][j]<inf) {ok++;break;}

判断是否能通过管道时，f[i][j]<inf开始写成f[i][j]!=inf

有可能在之前min（inf，inf）+1=inf+1

50分暴力代码：

#include<cstdio>

#include<algorithm>

using namespace std;

int n,m,k,jl,minn=,ans=;

int up[],down[],s[],x[];

bool have[];

void dfs(int pos,int now,int ope,int cross)

{

    jl=max(jl,cross);

    if(pos==n)

    {

        ans=min(ans,ope);

        return ;

    }

    int down_will=now-down[pos];

    int g=;

    while()

    {

        if(g>) return;

        if(now+up[pos]*g>=m)

        {

            if(!have[pos+]) dfs(pos+,m,ope+g,cross+have[pos]);

            break;

        }

        if(now+up[pos]*g>x[pos+]&&now+up[pos]*g<s[pos+]) dfs(pos+,now+up[pos]*g,ope+g,cross+have[pos]);

        else break;

        g++;

    }

    if(down_will>x[pos+]&&down_will<s[pos+]) dfs(pos+,down_will,ope,cross+have[pos]);

}

int main()

{

    freopen("birda.in","r",stdin);

    freopen("birda.out","w",stdout);

    scanf("%d%d%d",&n,&m,&k);

    for(int i=;i<n;i++) scanf("%d%d",&up[i],&down[i]);

    int a;

    for(int i=;i<=k;i++)

    {

        scanf("%d",&a);

        minn=min(a,minn);

        have[a]=true;

        scanf("%d%d",&x[a],&s[a]);

    }

    for(int i=;i<=n;i++)

     if(!have[i])

      x[i]=,s[i]=m+;

    for(int i=;i<=m;i++)

     dfs(,i,,);

    if(jl==k) printf("1\n%d",ans);

    else printf("0\n%d",jl);

}