Course Selection CodeChef - RIN

All submissions for this problem are available.

Read problems statements in Mandarin Chineseand Russian.

Rin is attending a university.

She has M semesters to finish her program, and that program has N required courses. Each course must be taken in exactly one of the semesters.

Some courses have prerequisites: for each i from 1 to K, she must take course A[i]before course B[i].

The same course may be taught by different professors in different semesters, and how well she does will depend on which professor teaches her. Additionally, some courses may not be taught every semester.

We are given an array X representing this information. For each course i and each semester j, X[i][j] = -1 if course i is not taught in semester j. Otherwise, X[i][j] will be an integer between 0 and 100: the expected score Rin will get if she takes course i in semester j.

Rin may take any number of courses per semester, including none, as long as they are taught that semester and she has already taken any required prerequisite courses.

Help Rin to find the maximal average score she can get over her whole program.

Input

The first line contain 3 integers: N, M and K.

This is followed by N lines, each containing M integers. The j^th integer on the i^th line represents the value of X[i][j].

This is followed by K lines, each containing two integers: A[i] and B[i].

Output

Output one real number: the maximal average score, rounded to 2 digits after the decimal point.

Constraints

• 1 ≤ M, N ≤ 100
• 0 ≤ K ≤ 100
• -1 ≤ X[i][j] ≤ 100
• 1 ≤ A[i], B[i] ≤ N
• For each i, A[i] ≠ B[i].
• For different i and j, (A[i], B[i]) ≠ (A[j], B[j]).
• We guarantee there exists a way to take these N courses in M semesters.

Subtasks

Subtask 1: (20 Points) A course can have at most 1 pre request course.

Subtask 2: (80 Points) Refer to constraints above

Example

Input 1:
3 2 2
70 100
100 80
100 90
1 2
1 3

Output 1:
80.00

Input 2:
4 5 4
20 -1 100 -1 -1
100 30 -1 -1 -1
100 -1 30 20 40
100 30 40 50 20
1 2
1 3
2 4
3 4

Output 2:
32.50

Explanation

Example case 1

The only way she can finish these 3 courses is: take course 1 in the first semester, then take courses 2 and 3 in the second semester. The average score is (70 + 80 + 90) / 3 = 80.00.

Example case 2

The optimal solution is: take course 1 in semester 1, course 2 in semester 2, course 3 in semester 3 and course 4 in semester 4.

EXPLANATION:

First, let's ignore the dependencies. The answer is just the maximum grade per course in any of the semesters, which is trivial to compute but let's put this in another perspective:

For each course, the best grade is 100 - (minimum grade we lose by picking one of the semesters).

To model this as a network flow graph, we do 4 things:

1. Create a vertex for each pair (course i, semester j).
2. Create a source vertex which is connected to the first semester of each course i by an edge with capacity 100 - grade(i, 1).
3. For every semester j from 2 to M, connect the vertices of each course i from semester j-1 to j with capacity 100 - grade(i, j) or 100 if the course is not available (it's the same as having grade 0, recall that it's guaranteed there is a solution).
4. Create a sink vertex and connect the last semester of each course to it, with infinite capacity.

Consider the following example with 3 courses and 3 semesters:

3 3
10 70 100
80 50 40
80 20 40

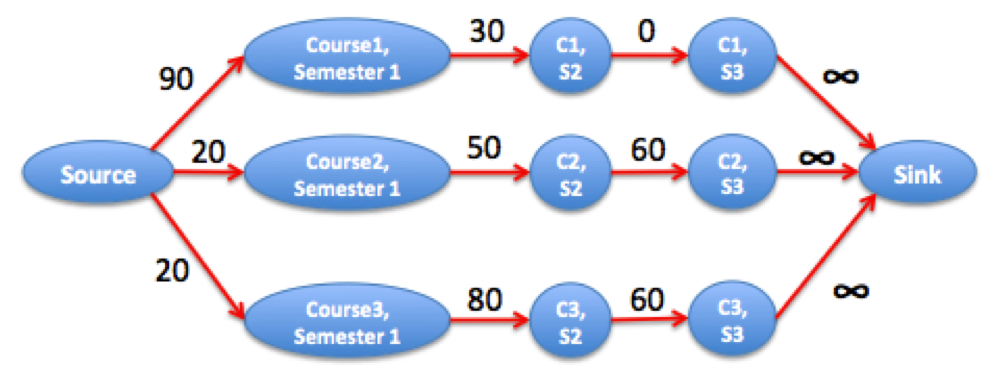
The corresponding graph is depicted in the above picture. The maximum flow is equal to the combined grade loss for all courses. We pick semester 3 for course 1 (zero loss), and semester 1 for courses 2 and 3 (loss 20+20). The maximum grade average we can get is (N * 100 - maxflow) / N. In this case: (3*100 - 40) / 3 ~= 86.67.

- Returning to the problem, why does this help?

If we model the problem this way, we can also include the course dependencies. Suppose there are dependencies 1->2 and 1->3. The best we can do is course 1 in semester 2 and courses 2 and 3 in semester 3 for (70+40+40)/3 average.

- If there are dependencies 1->2 and 1->3, then courses 2 and 3 can never be done in the first semester.

This implies that the minimum grade loss for courses 2 and 3 is not bounded by its grades in semester 1. This is the same as changing the capacities associated to semester 1 of courses 2 and 3 to infinity.

- Why do we pick semester j for course 1?

The combined grade loss of doing course 1 in semester 2 + courses 2 and 3 in semester 3 is less than doing course 1 in semester 1 + courses 2 and 3 in semesters 2 or 3.

In terms of network flow, this means that

• if we pick semester j = 1, then courses 2 and 3 are not bounded by grade loss in semester 1. To combine the grade loss by picking semester 1, we connect vertex (course 1, semester 1) to (course 2, semester 2) and (course 3, semester 2) with infinite capacity.
• if we pick semester j = 2, then courses 2 and 3 are not bounded by grade loss in semesters 1 and 2. Same as above but connecting (course 1, semester 2) to courses 2 and 3, semester 3.
• picking semester j = 3 is not possible.

The resulting network is the following

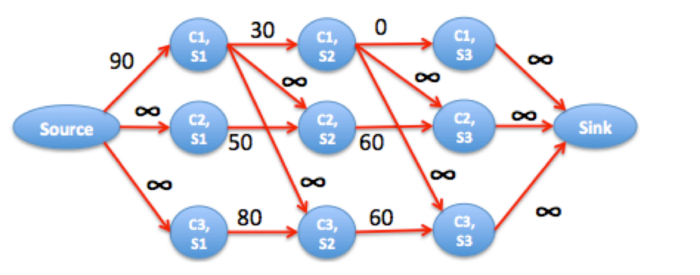
We can see that the maximum flow is 150. The best is to distribute the grade loss of course 1 in semester 2, flow 3, among courses 2 and 3 in semester 3. In fact, 70+40+40 = 300 - 150.

To give you another example, consider the input

3 3 2
10 50 100
80 90 40
80 40 70
1 2
1 3

The best we can do course 1 at semester 1 (10) + course 2 at semester 2 (90) and course 3 at semester 3 (70) = 10+90+70. The resulting graph is

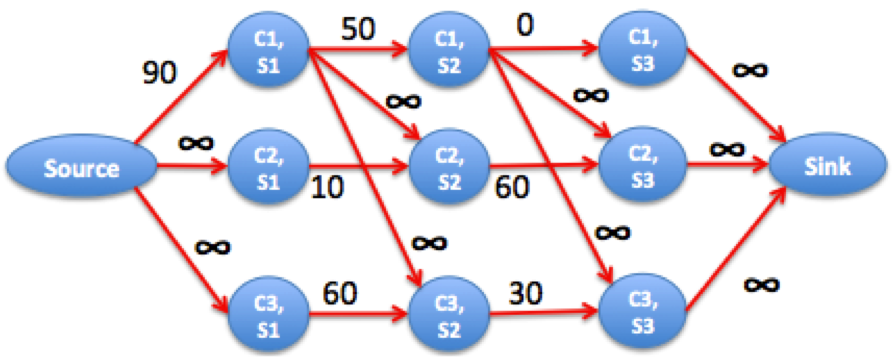
We can see that the maximum flow is 130 because in this case, it is better to distribute the grade loss of course 1 at semester 1, the flow 90, among the grade loss of courses 2 and 3 over semesters 2 and 3, respectively.

In a nutshell, we create a graph with N*M+2 vertices and use a standard maximum flow algorithm. The hard part was to realize how to build the network correctly.

Proof sketch:

Since max-flow equals min-cut, we can think of our problem as of finding a minimum cut in the above graph. Let P_i be a path corresponding to i-th course, i.e. the path formed of edges corresponding to i-th course in all semesters. In order to prove the correction of the above construction, we can show two properties of the graph:

1. For every 1 <= i <= N, min-cut contains exactly one edge from P_i.
2. For every constraint (i, j), if min-cut contains the k-th edge of P_i, then it contains the x-th edge of P_j, where x > k i.e. j-th course is taken in later semester than i-th course.

These two fact can be shown quite easily, but we will omit exact proofs here. Intuitively, if you pick any edge from P_i, then P_i is disconnected and there is no need for taking any other edge from it. Moreover, an edge (i, j) corresponding to a constraint, prevent us of taking course j before course i, because if you did it, then in order to make the graph disconnected, you would have to add the second edge of P_j to min-cut which contradicts the first fact.

Select Code

#include<cstdio>
#include<cstring>
#include<iostream>
#define inf 2e9
using namespace std;
const int Z=101;
const int N=Z*Z;
const int M=2e6+5;
struct edge{int v,next,cap;}e[M];int tot=1,head[N];
int n,m,k,cnt,ans,S,T,id[Z][Z],X[Z][Z],dis[N],q[M];
inline int read(){
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
inline void add(int x,int y,int z){
	e[++tot].v=y;e[tot].cap=z;e[tot].next=head[x];head[x]=tot;
	e[++tot].v=x;e[tot].cap=0;e[tot].next=head[y];head[y]=tot;
}
inline bool bfs(){
	for(int i=S;i<=T;i++) dis[i]=-1;
	int h=0,t=1;q[t]=S;dis[S]=0;
	while(h!=t){
		int x=q[++h];
		for(int i=head[x];i;i=e[i].next){
			if(e[i].cap&&dis[e[i].v]==-1){
				dis[e[i].v]=dis[x]+1;
				if(e[i].v==T) return 1;
				q[++t]=e[i].v;
			}
		}
	}
	return 0;
}
int dfs(int x,int f){
	if(x==T) return f;
	int used=0,t;
	for(int i=head[x];i;i=e[i].next){
		if(e[i].cap&&dis[e[i].v]==dis[x]+1){
			t=dfs(e[i].v,min(e[i].cap,f));
			e[i].cap-=t;e[i^1].cap+=t;
			used+=t;f-=t;
			if(!f) return used;
		}
	}
	if(!used) dis[x]=-1;
	return used;
}
inline void dinic(){
	while(bfs()) ans-=dfs(S,inf);
}
inline int getY(int x){
	if(~x) return 100-x;
	return inf;
}
int main(){
	n=read();m=read();k=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			X[i][j]=read();
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			id[i][j]=++cnt;
		}
	}
	S=0,T=n*m+1;
	for(int i=1;i<=n;i++){
		add(S,id[i][1],getY(X[i][1]));
		for(int j=2;j<=m;j++) add(id[i][j-1],id[i][j],getY(X[i][j]));
		add(id[i][m],T,inf);
	}
	for(int i=1,a,b;i<=k;i++){
		a=read();b=read();
		add(S,id[b][1],inf);
		for(int j=2;j<=m;j++) add(id[a][j-1],id[b][j],inf);
	}
	ans=100*n;
	dinic();
	printf("%.2lf",1.0*ans/n);
	return 0;
}