PID控制器开发笔记之十三：单神经元PID控制器的实现

　　神经网络是模拟人脑思维方式的数学模型。神经网络是智能控制的一个重要分支，人们针对控制过程提供了各种实现方式，在本节我们主要讨论一下采用单神经元实现PID控制器的方式。

1、单神经元的基本原理

　　单神经元作为构成神经网络的基本单位，具有自学习和自适应能力，且结构简单而易于计算。接下来我们讨论一下单神经元模型的基本原理。

（1）、单神经元模型

　　所谓单神经元模型，是对人脑神经元进行抽象简化后得到一种称为McCulloch-Pitts模型的人工神经元，如下图所示。

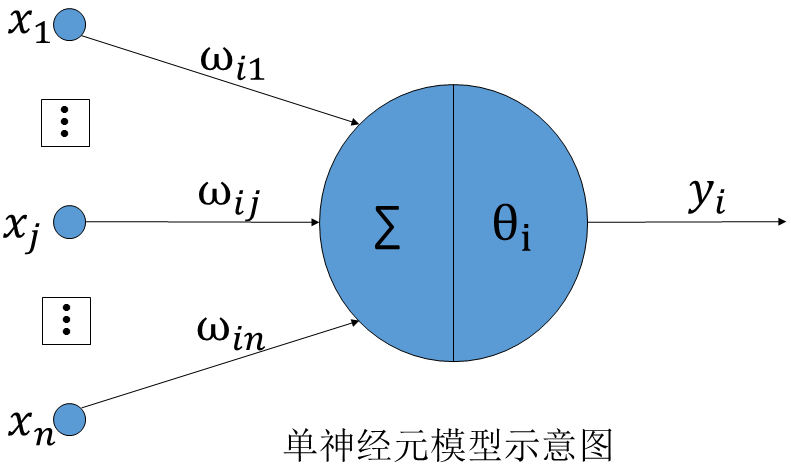
　　根据上图所示，对于第i个神经元，x₁、x₂、……、x_N是神经元接收到的信息，ω₁、ω₂、……、ω_N为连接强度，又称之为权。采用某种运算方式把输入信号的作用结合起来，得到他们总的结果，称之为“净输入”通常用net_i表示。根据所采用的运算方式的不同，净输入有不同的表示形式，比较常用的是线性加权求和，其表达式如下：

　　其中，θi是神经元i的阈值。

　　而神经元i的输出yi可以表示为其当前状态的函数，这个函数我们称之为激活函数。一般表示如下：

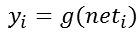
（2）、采用的学习规则

　　学习是神经网络的基本特征，而学习规则是实现学习过程的基本手段。学习规则主要实现对神经元之间连接强度的修正，即修改加权值。而学习过程可分为有监督学习和无监督学习两类。它们的区别简单的说，就是是否引入期望输出参与学习过程，引入了则称之为有督导学习。较为常用的学习规则有三种：

a、无监督Hebb学习规则

　　Hebb学习是一类相关学习，它的基本思想是：如果神经元同时兴奋，则它们之间的连接强度的增强与它们的激励的乘积成正比。以Oi表示单元i的激活值，以Oj表示单元j的激活值，以ωij表示单元j到单元i的连接强度，则Hebb学习规则可用下式表示：

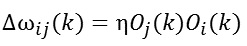
b、有监督Delta学习规则

　　在Hebb学习规则中，引入教师信号，将式Oj换成网络期望目标输出dj和网络实际输出Oj之差，即为有监督Delta学习规则，即：

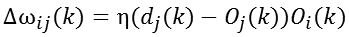
c、有监督Hebb学习规则

　　将无监督Hebb学习规则和有监督Delta学习规则两者结合起来，就组成有监督Hebb学习规则，即：

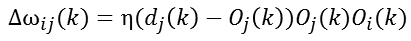
　　在以上各式中，η称之为学习速度。

2、单神经元PID的基本原理

　　在前面我们说明了单神经元的基本原理，接下来我们讨论如何将其应用的PID控制中。前面我们已经知道了神经元的输入输出关系，在这里我们考虑PID算法的增量型表达式：

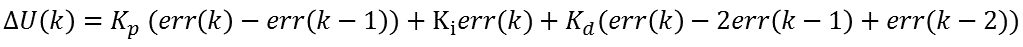
　　若是我们记：x1(k)=err(k)，x2(k)=err(k)- err(k-1)，x3(k)=err(k)- 2err(k-1)+err(k-2)，同时将比例、积分、微分系数看作是它们对应的加权，并记为ωi(k)。同时我们引进一个比例系数K，则可将PID算法的增量型公式改为：

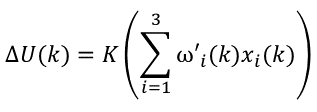
　　其中，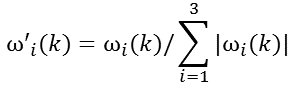

　　我们将PID的增量公式已经改为单神经元的输入输出表达形式，还需要引进相应的学习规则就可以得到单神经元PID控制器了。在这里我们采用有监督Hebb学习规则于是可以得到学习过程：

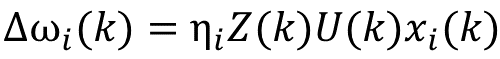
　　从学习规则的定义，我们知道在上式中，Z(k)= err(k)。而U(k)= U(k-1)+∆U(k)，ω(k)= ω(k-1)+∆ω(k)。到这里实际上已经得到了单神经元PID的算法描述。

3、单神经元PID的软件实现

　　有了前面的准备，我们就可以开始编写基于单神经元的PID控制程序了。首先依然是定义一个单神经元的PID结构体：

 /*定义结构体和公用体*/
 
 typedef struct
 
 {
 
   float setpoint;               /*设定值*/
 
   float kcoef;                  /*神经元输出比例*/
 
   float kp;                     /*比例学习速度*/
 
   float ki;                     /*积分学习速度*/
 
   float kd;                     /*微分学习速度*/
 
   float lasterror;              /*前一拍偏差*/
 
   float preerror;               /*前两拍偏差*/
 
   float deadband;               /*死区*/
 
   float result;                 /*输出值*/
 
   float output;                 /*百分比输出值*/
 
   float maximum;                /*输出值的上限*/
 
   float minimum;                /*输出值的下限*/
 
   float wp;                     /*比例加权系数*/
 
   float wi;                     /*积分加权系数*/
 
   float wd;                     /*微分加权系数*/
 
 }NEURALPID;

　　接下来在使用PID对象之前依然需要对它进行初始化操作，以保证在未修改参数的值之前，PID对象也是可用的。这部分初始化比较简单，与前面的各类PID对象的初始化类似。

 /* 单神经元PID初始化操作,需在对vPID对象的值进行修改前完成                     */
 
 /* NEURALPID vPID，单神经元PID对象变量，实现数据交换与保存                    */
 
 /* float vMax,float vMin，过程变量的最大最小值（量程范围）                    */
 
 void NeuralPIDInitialization(NEURALPID *vPID,float vMax,float vMin)
 
 {
 
   vPID->setpoint=vMin;                  /*设定值*/
 
   vPID->kcoef=0.12; /*神经元输出比例*/
 
   vPID->kp=0.4;                         /*比例学习速度*/
 
   vPID->ki=0.35;                        /*积分学习速度*/
 
   vPID->kd=0.4;                         /*微分学习速度*/
 
   vPID->lasterror=0.0;                  /*前一拍偏差*/
 
   vPID->preerror=0.0;                   /*前两拍偏差*/
 
   vPID->result=vMin;                    /*PID控制器结果*/
 
   vPID->output=0.0;                     /*输出值，百分比*/
 
   vPID->maximum=vMax;                   /*输出值上限*/
 
   vPID->minimum=vMin;                   /*输出值下限*/  
 
   vPID->deadband=(vMax-vMin)*0.0005;    /*死区*/
 
   vPID->wp=0.10; /*比例加权系数*/
 
   vPID->wi=0.10; /*积分加权系数*/
 
   vPID->wd=0.10; /*微分加权系数*/
 
 }

　　初始化之后，我们就可以调用该对象进行单神经元PID调节了。前面我们已经描述过算法，下面我们来实现它：

 /* 神经网络参数自整定PID控制器，以增量型方式实现                              */
 
 /* NEURALPID vPID，神经网络PID对象变量，实现数据交换与保存                    */
 
 /* float pv，过程测量值，对象响应的测量数据，用于控制反馈                     */
 
 void NeuralPID(NEURALPID *vPID,float pv)
 
 {
 
   float x[];
 
   float w[];
 
   float sabs
 
   float error;
 
   float result;
 
   float deltaResult;
 
   error=vPID->setpoint-pv;
 
   result=vPID->result;
 
   if(fabs(error)>vPID->deadband)
 
   {
 
     x[]=error;
 
     x[]=error-vPID->lasterror;
 
     x[]=error-vPID->lasterror*+vPID->preerror;
 
     sabs=fabs(vPID->wi)+fabs(vPID->wp)+fabs(vPID->wd);
 
     w[]=vPID->wi/sabs;
 
     w[]=vPID->wp/sabs;
 
     w[]=vPID->wd/sabs;
 
     deltaResult=(w[]*x[]+w[]*x[]+w[]*x[])*vPID->kcoef;
 
     }
 
   else
 
   {
 
     deltaResult=;
 
   }
 
   result=result+deltaResult;
 
   if(result>vPID->maximum)
 
   {
 
     result=vPID->maximum;
 
   }
 
   if(result<vPID->minimum)
 
   {
 
     result=vPID->minimum;
 
   }
 
   vPID->result=result;
 
   vPID->output=(vPID->result-vPID->minimum)*/(vPID->maximum-vPID->minimum);
 
   //单神经元学习
 
   NeureLearningRules(vPID,error,result,x);
 
   vPID->preerror=vPID->lasterror;
 
   vPID->lasterror=error;
 
 }

　　前面的算法分析中，我们就是将增量型PID算法的表达式转化为单神经元PID公式的。二者最根本的区别在于单神经元的学习规则算法，我们采用了有监督Hebb学习规则来实现。

 /*单神经元学习规则函数*/
 
 static void NeureLearningRules(NEURALPID *vPID,float zk,float uk,float *xi)
 
 {
 
   vPID->wi=vPID->wi+vPID->ki*zk*uk*xi[];
 
   vPID->wp=vPID->wp+vPID->kp*zk*uk*xi[];
 
   vPID->wd=vPID->wd+vPID->kd*zk*uk*xi[];
 
 }

　　至此，单神经元PID算法就实现了，当然有很多进一步优化的方式，都是对学习规则算法的改进，因为改进了学习规则，自然就改进了单神经元PID算法。

4、单神经元PID总结

　　前面我们已经分析并实现了单神经元PID控制器，在本节我们来对它做一个简单的总结。

　　与普通的PID控制器一样，参数的选择对调节的效果有很大影响。对单神经元PID控制器来说，主要是4个参数：K、ηp、ηi、ηd，我们总结一下相关参数选取的一般规律。

　　（1）对连接强度（权重ω）初始值的选择并无特殊要求。

　　（2）对阶跃输入，若输出有大的超调，且多次出现正弦衰减现象，应减少增益系数K，维持学习速率ηp、ηi、ηd不变。若上升时间长，而且无超调，应增大增益系数K以及学习速率ηp、ηi、ηd。

　　（3）对阶跃输入，若被控对象产生多次正弦衰减现象，应减少比例学习速率ηp，而其它参数保持不变。

　　（4）若被控对象响应特性出现上升时间短，有过大超调，应减少积分学习速率ηi，而其它参数保持不变。

　　（5）若被控对象上升时间长，增大积分学习速率ηi又会导致超调过大，可适当增加比例学习速率ηp，而其它参数保持不变。

　　（6）在开始调整时，微分学习速率ηd应选择较小值，在调整比例学习速率ηp、积分学习速率ηi和增益系数K使被控对象达到较好特性后，再逐渐增加微分学习速率ηd，而其它参数保持不变。

　　（7）K是系统最敏感的参数，K值的变化相当于P、I、D三项同时变化。应在开始时首先调整K，然后再根据需要调整学习速率。

　　在单神经元PID控制器中，上述这些参数对调节效果的影响如何呢？一般情况下具有如下规律。

　　（1）在积分学习率、微分学习率不变的情况下，比例系数学习率越大则超调量越小，但是响应速度也会越慢；

　　（2）在比例学习率、微分学习率不变的情况下，积分系数学习率越大则响应会越快，但是超调量也会越大。

　　（3）在比例学习率、积分学习率不变的情况下，微分学习率对单神经元PID控制器的控制效果影响不大。

　　最后我们需要明白，单神经元PID算法是利用单神经元的学习特性，来智能的调整PID控制过程。单神经元可以实现自学习，这正好可以弥补传统PID算法的不足。正如前面所说，学习是它的最大特点，那么不同的学习算法对其性能的影响会很大，所以改进学习规则算法对提高性能有很大帮助。

 欢迎关注：