BZOJ3434 [Wc2014]时空穿梭

本文版权归ljh2000和博客园共有，欢迎转载，但须保留此声明，并给出原文链接，谢谢合作。

本文作者：ljh2000
作者博客：http://www.cnblogs.com/ljh2000-jump/
转载请注明出处，侵权必究，保留最终解释权！

Description

Input

第一行包含一个正整数T，表示有T组数据求解
每组数据包含两行，第一行包含两个正整数N,C(c>=2),分别表示空间的
维数和需要选择的暂停点个数
第二行包含N个正整数，依次表示M1,M2....Mn

Output

有T行，每行一个非负整数，依次对应每组数据的答案。

Sample Input

3
2 3
3 4
3 3
3 4 4
4 4
5 9 7 8

Sample Output

2
4
846

HINT

样例数据第一组共有两种可行方案：一种是选择（1,1），（ 2,2） ,（ 3,3） ，另一种是选择 （ 1,2） ,（ 2,3） ,（ 3,4） 。

T<=1000,N<=11,C<=20,Mi<=100000

正解：莫比乌斯反演+组合数学

解题报告：

　　 下面摘自我校学长rhl的solution：

　　  到这一步应该是很好推的，然而我并没有一开始就想出来。

　　第一行是原始的式子，然后我们考虑变枚举每个△x的值，枚举每个gcd（不妨设为g）的贡献，则可得到第二行式子，注意这个式子满足当且仅当每个△x的gcd为1；

　　第二行到第三行是莫比乌斯函数的应用：莫比乌斯函数前缀和为1当且仅当n=1。显然前缀和为1的时候说明t只能取1，也就是说△x的gcd为1。

　　下面是进一步的推导：

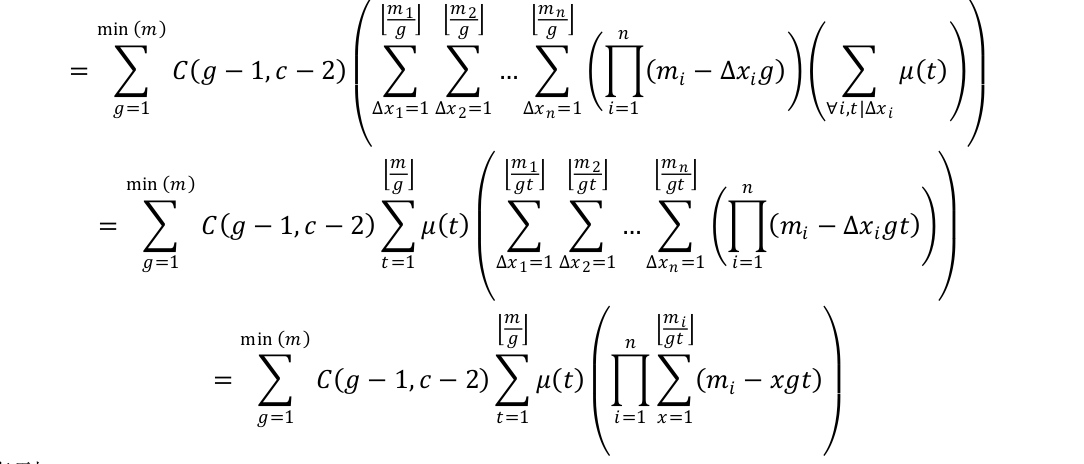
　　 容易发现从图中第一行到第二行是提出了t，提出t的方式我们可以这样理解：

　　把t的莫比乌斯函数前缀和看成一个整体，那么我枚举△x再枚举t，可以等价于先枚举t再去枚举当前的这个t所产生的贡献，所以△x的范围中再用t去约束。而因为t的最大值肯定是在最小的那个m中取到，所以最大值就是$\left\lfloor\frac{m}{g}\right\rfloor$。

　　第二行到第三行，相当于是用了一次乘法分配律。可以想象有n列数，每列数就是对应着每个△x的取值范围，第二行的那一块相当于是每一列中取一个数然后一一对应，就可以变成每个数先加起来再乘。以$n=2$为例，△x1取第一个值的时候，△x2可以取第二列的所有值，然后△x1的这一个值和所有的△x2的取值分别组合，就可以先对于△x2求和再乘上△x1的那个唯一取值即可，而每个△x1的取值都是对应的与每个△x2组合，所以△x1的部分也可以求和。就变成了上面的式子长得那样。

　　

　　

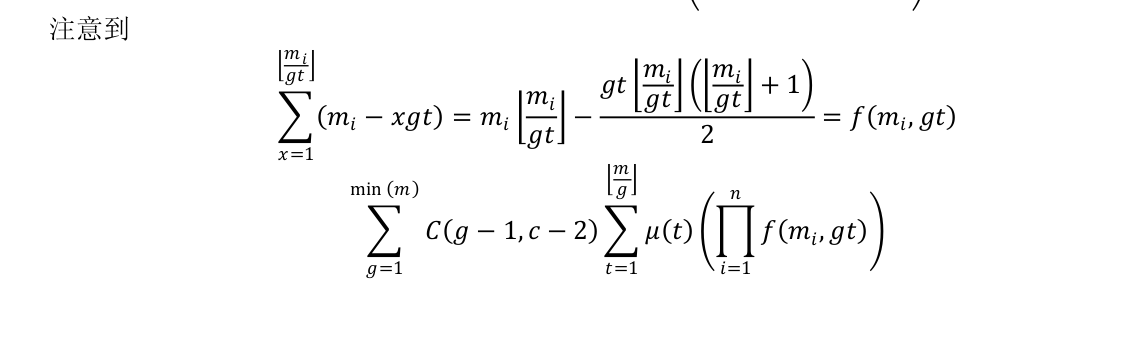
　　　第二行到第三行，同样可以理解成乘法分配率。不难想象，拆开之后每一项都是形如$f$项的未知数是$gt$，组合数C的是$g$，莫比乌斯函数μ的是$t$。那么我可以采用惯用策略：计算$f$项的贡献，不妨设$h=g*t$，同时枚举一个$g$，那么$h/g$就是原来的$t$，想想就会发现这样可以覆盖到所有的情况，也就是说这样枚举的话就可以把$h$项的贡献计算完成了。

　　得到第五行的式子之后，就可以得到一个$O(nm)$的算法，看了看数据范围，应该有$60$分了。然而我试了试只有50分，看来我也变成常数boy了。

　　

　　　接下来我们考虑如何优化上式：

　　

　　

　　如图中所述，函数是由若干段构成的，那么每一段都可以一起计算，最后加在一起就可以了。

　　到此为止就算over了。　　

　　总结一下：

　　

　　

　　　　　　

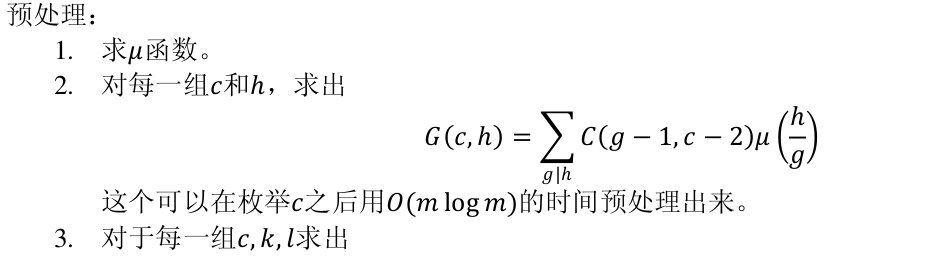
　　推导+调试用了我两天时间！！！一把辛酸泪

　　

//It is made by ljh2000
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <string>
using namespace std;
typedef long long LL;
const int MAXN = 12;
const int inf = (1<<30);
const int MAXL = 100011;
const int MAXM = 4000011;
const int MOD = 10007;
int n,c,m[MAXN],prime[MAXL],Mc,mobius[MAXL],cnt,mn,mx,C[MAXL][21],ans,G[21][MAXL],f[21][12][MAXL],a[MAXN];
bool vis[MAXL];
namespace save{ int n[1011],c[1011]; int m[1011][12]; }
inline void MO(int &x){ if(x>MOD) x%=MOD; else if(x<-MOD) x%=MOD; }
inline int getint(){
    int w=0,q=0; char c=getchar(); while((c<'0'||c>'9') && c!='-') c=getchar();
    if(c=='-') q=1,c=getchar(); while (c>='0'&&c<='9') w=w*10+c-'0',c=getchar(); return q?-w:w;
}

inline void init(){
	mobius[1]=1; int lim=Mc-2,x;
	for(int i=2;i<=mx;i++) {//线性筛+递推莫比乌斯函数
		if(!vis[i]) { mobius[i]=-1; prime[++cnt]=i; }
		for(int j=1;j<=cnt&&i*prime[j]<=mx;j++) {
			vis[i*prime[j]]=1;
			if(i%prime[j]) mobius[i*prime[j]]=-mobius[i];
			else { mobius[i*prime[j]]=0; break; }
		}
	}
	C[0][0]=1; for(int i=1;i<=mx;i++){ C[i][0]=1; for(int j=1;j<=lim;j++) C[i][j]=C[i-1][j-1]+C[i-1][j],MO(C[i][j]); }
	for(int cc=2;cc<=Mc;cc++) {//预处理G数组,G[cc][i]表示c=cc、h=i时的G(h)的值
		for(int i=1;i<=mx;i++) {
			for(int j=i,ci=1;j<=mx;j+=i,ci++) {
				G[cc][j]+=C[i-1][cc-2]*mobius[ci];
				MO(G[cc][j]);
			}
		}
	}
	for(int h=1;h<=mx;h++) {//f[cc][j][i]表示G(h)*h^j中1到h的前缀和，固定指数！
		for(int cc=1;cc<=Mc;cc++) {
			x=1;
			for(int j=0;j<=11;j++) {
				f[cc][j][h]=G[cc][h]*x+f[cc][j][h-1]; MO(f[cc][j][h]);
				x*=h; MO(x);
			}
		}
	}
}

inline void cal(int h){//若干个形如(px+q)的一次式相乘
	int x1,x0,t; memset(a,0,sizeof(a)); a[0]=1;//初始化
	for(int i=1;i<=n;i++) {
		t=(m[i]/h);
		x1=( -(LL)t*(t+1)/2 )%MOD;//计算p，注意有一个负号
		x0=( (LL)m[i]*t )%MOD;//计算q
		for(int j=n;j>=1;j--)
			a[j]=a[j]*x0+a[j-1]*x1,MO(a[j]);//第j次项可以由上次的第j-1次项*px，也可以由上次的第j项*q得到
		a[0]=a[0]*x0;//0次项单独考虑
		MO(a[0]);
	}
}

inline void work(){
	int T=getint();
	for(int o=1;o<=T;o++) {
		save::n[o]=getint(),save::c[o]=getint(); Mc=max(save::c[o],Mc);
		for(int i=1;i<=save::n[o];i++) save::m[o][i]=getint(),mx=max(mx,save::m[o][i]);
	}
	init();
	for(int o=1;o<=T;o++) {
		n=save::n[o]; c=save::c[o]; mn=inf;//最小的m
		for(int i=1;i<=n;i++) m[i]=save::m[o][i],mn=min(mn,m[i]);
		ans=0; int nex;
		for(int i=1;i<=mn;i=nex+1) {
			nex=mn; for(int j=1;j<=n;j++) nex=min(nex,m[j]/(m[j]/i));
			cal(i);	for(int j=0;j<=n;j++) ans+=a[j]*(f[c][j][nex]-f[c][j][i-1]),MO(ans);
		}
		ans%=MOD; ans+=MOD; ans%=MOD;
		printf("%d\n",ans);
	}
}

int main()
{
    work();
    return 0;
}