[jzoj]3456.【NOIP2013模拟联考3】恭介的法则(rule)

Link

　　https://jzoj.net/senior/#main/show/3456

Description

　　终于，在众亲们的奋斗下，最终boss 恭介被关进了库特设计的密室。正当她们松了一口气时，这个世界却发生了天翻覆地的变化：地面开始下沉，天空开始变成血红色，海水沸腾……一幅世界末日的图景。美鱼从她手中的古籍《若山牧水诗歌集》中发现了原因：白鸟は かなしからずや 空の青 海のあをにも 染まずただよふ 。大（xia）意（shuo）就是狡猾的恭介在创造这个世界的时候就篡改了法则。而这个法则的起源，就是一只生死之间的猫。这个猫被关在一个黑盒子里，盒子里有两个毒气罐，如果有任意一个毒气罐被打开那么猫将会被杀死，法则也能得到纠正。然而外界能控制的仅仅是这两个毒气罐被打开的概率。假设第一个毒气罐被打开的概率为1/x，第二个毒气罐为1/y（x,y 为正整数），那么当两个概率和为1/(n!)时，猫将会被莫名其妙地杀死。现在美鱼想知道，有多少对(x,y)可以让猫被莫名其妙杀死。

Solution

　　其实，题目大意可以直接转化成如下一句精炼的话。

　　

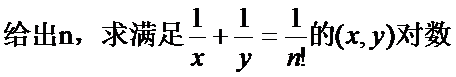
30分

　　显然，因为n太小了，最大只有6，打表都行了，反正我考试时n=6也超时。。

60分

　　正解+傻到没打高精度，或者打表。

100分

　　我们分解一下题目给出的式子，详见下面过程及讲解

　　合并左边的分式可得

　　

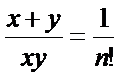
　　通过交叉相乘可得

　　

　　通过乘法分配律的逆运算得

　　

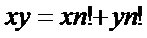
　　移项得

　　

　　通过合并式子得

　　

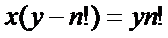
　　移项得

　　

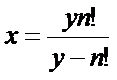
　　分解到这里，我们可以推出下面的式子

　　

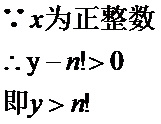
　　x同样可以这样证出来，我考试一直在证这个，其实还是有些乱用的，但是后面才是重点

　　根据数学归纳，可以得知，x或y的最大值为n!(n!+1)，虽然这没什么卵用

　　我们枚举y来确定x，显然

　　

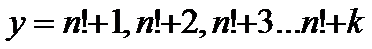
　　我们将y表示为一般的形式，即y=n!+k(k代表任意符合条件的数)，带入前面的式子中，得

　　

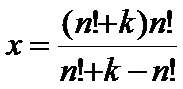
　　合并同类项化简得　　

　　

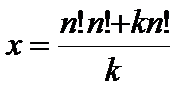
　　因为x是整数，所以n!n!+kn!必定为k的倍数，因为kn!是k的倍数，故不必考虑第二个多项式，我们只要考虑第一个多项式，即满足如下条件

　　

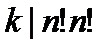
　　这样，答案就转化成求n!n!的约数个数了

　　快速求n!的约数个数和分解质因子出来的式子（包括质因子和其指数），可以看我写的博客，链接如下

　　（当成这里是有链接）

　　显然，我们知道一个数分解质因子出来的式子，那么这个数的平方的式子同样可以得出来，不过就是指数都乘2罢了

　　约数个数的公式就不用说了吧，小学一年级我就会了。

　　这里算约数个数需要高精度。

　　因为有时间限制，所以高精度要加常数优化，诸如低精度乘高精度，压位，延迟去乘法等

　　问题迎刃而解了，考试时我以为很屌很屌，实际上真的很屌很屌，我数学不好，特别是这种分解的然后用的数代替成一般形式的，Orz lyl,dyp,wmz大佬

Code

var
        now:int64;
        n,i,j,num,tot:longint;
        a:array[..] of int64;
        bz:array[..] of ..;
procedure gg(x:int64);
var
        i,len:longint;
begin
        for i:= to a[] do
                a[i]:=a[i]*x;

        len:=a[];
        i:=;

        while i<=len do
        begin
                a[i+]:=a[i+]+a[i] div ;
                a[i]:=a[i] mod ;

                if (a[i+]>) and (i+>len) then
                        inc(len);

                inc(i);
        end;

        a[]:=len;
end;
begin
        readln(n);

        a[]:=;
        a[]:=;
        now:=;

        for i:= to n do
                if bz[i]= then
                begin
                        for j:= to n div i do
                                bz[i*j]:=;

                        num:=n;
                        tot:=;

                        while num>=i do
                        begin
                                num:=num div i;

                                inc(tot,num);
                        end;

                        tot:=tot*+;

                        if now*tot> then
                        begin
                                gg(now);

                                now:=;
                        end;

                        now:=now*tot;

                end;

        if now<> then
                gg(now);

        write(a[a[]]);

        for i:=a[]- downto  do
                if a[i]>= then write(a[i]) else
                if a[i]>= then write('',a[i]) else
                if a[i]>= then write('',a[i]) else
                if a[i]>= then write('',a[i]) else
                if a[i]>= then write('',a[i]) else
                if a[i]>= then write('',a[i]) else
                if a[i]>= then write('',a[i]) else
                if a[i]>= then write('',a[i]) else
                if a[i]>= then write('',a[i]) else
                                write('',a[i]);
end.